关于线性表的学习总结
定义：具有相同数据类型的n个数据元素的有限序列。
线性表知识图谱如下：
顺序表
1.定义
#define Maxsize 100 //定义最大容量
typedef struct
{
Elemtype data; //顺序表数据
int length; //顺序表长度
}Sqlist;
2.顺序表的操作
①插入
分析：
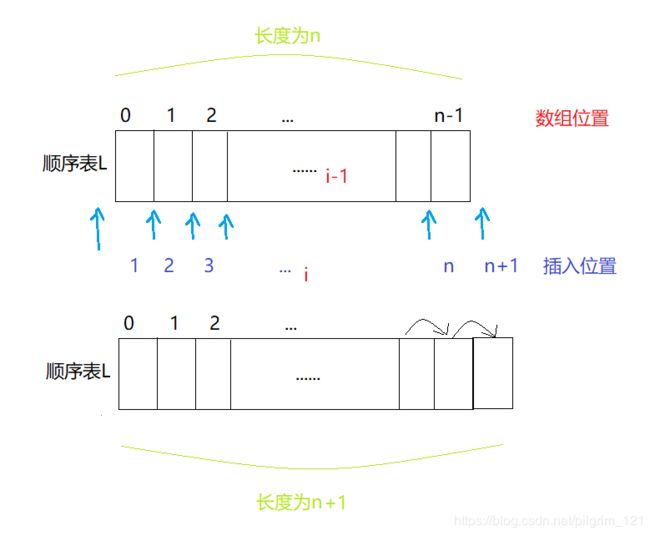
当顺序表长度为n时，插入位置有n+1个；数组下标比插入位置下标小1。
数组下标范围：0至n-1；插入位置范围：1至n+1。插入位置为1时，数组需要移动n个元素;
插入位置为2时，数组需要移动n-1个元素;
插入位置为i时，数组需要移动n-i+1个元素;
插入位置为n时，数组需要移动1个元素;
插入位置为n+1时，数组不需要移动元素;插入操作元素平均移动次数为：(n+(n-1)+…+2+1)/(n+1)=n/2
时间复杂度为O(n)。
代码：
bool InsertList(Sqlist &L,Elemtype e) //将e插入顺序表L中的第i个位置
{
//注意：插入位置范围是1~n+1
//这里L.length=n
if(i<1||i>L.length+1)// 插入位置非法
return false;
else
{
for(int j=L.length;j>=i;j--)//元素从后向前依次后移
L.data[j]=L.data[j-1];
L.data[i-1]=e;//在第i个位置插入e
L.length++;//顺序表长度加1
return true;
}
}
②删除
分析：
当顺序表长度为n时，删除位置有n个。
数组下标范围：0至n-1；删除位置范围：1至n。删除位置为1时，数组需要移动n-1个元素;
删除位置为2时，数组需要移动n-2个元素;
删除位置为i时，数组需要移动n-i个元素;
删除位置为n时，数组不需要移动元素;删除操作元素平均移动次数为：((n-1)+…+2+1)/(n+1)=(n-1)/2
时间复杂度为O(n)。
代码：
bool DeleteList(Sqlist &L,int i,Elemtype &e) //删除顺序表中的第i个元素，并用e返回值
{
//注意：插入位置范围是1~n
if(i<1||i>L.length)
return false;
else
{
e=L.data[i-1];//第i个位置元素的值
for(int j=i;j③按值查找某个元素的位置
分析：
当顺序表长度为n时，查找位置有n个。
数组下标范围：0至n-1；查找位置范围：1至n。数组下标为0时，需要查找1次;
数组下标为1时，需要查找2次;
数组下标为i-1时，需要查找i次;
数组下标为n-1时，需要查找n次查找操作元素平均查找次数为：(n+…+2+1)/n=(n+1)/2
时间复杂度为O(n)。
代码：
int LocateElem(Sqlist L,Elemtype e) //查找e在顺序表中的位置
{
for(int i=0;i链表
链表之单链表
1.定义
typedef struct LNode
{
Elemtype data;//数据域
struct LNode *next;//指针域
}LNode,*LinkList;
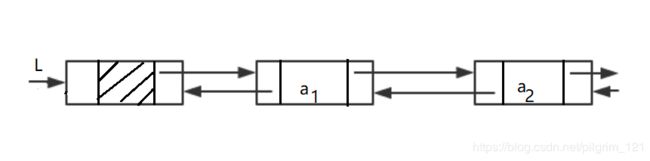
2.关于头指针与头节点
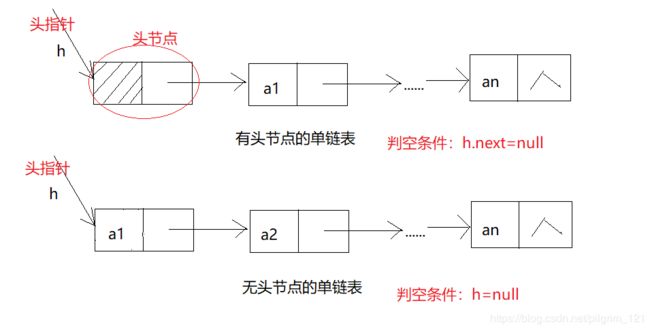
通常，用头指针来标识一个链表。引入头节点后，运算(图中a1和其它节点一样，不用特殊处理.)更加方便。
3.单链表的基本操作
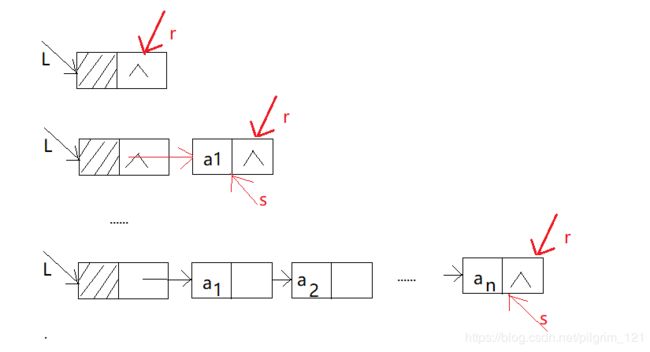
①建立单链表之头插法
代码：
Linklist Create_head(Linklist &L)
{
L=(Linklist)malloc(sizeof(LNode));//创建头节点
L→next=null;
LNode *s;//指向待插入的节点
Elemtype e;
scanf("%d",&e);
while(e!="#")
{
s=(LNode)malloc(sizeof(LNode));//创建节点s
s→data=e;//插入节点s
s→next=L→next;
L→next=s;
scanf("%d",&e);//输入e，继续判断
}
return L;
}
②建立单链表之尾插法
代码：
Linklist Create_tail(Linklist &L)
{
L=(Linklist)malloc(sizeof(LNode));//创建头节点
L→next=null;
LNode *s;//指向待插入的节点
LNode *r;//指向尾节点
r=L;//初始时尾指针也指向头节点
Elemtype e;
scanf("%d",&e);
while(e!="#")
{
s=(LNode)malloc(sizeof(LNode));//创建节点s
s→data=e;//插入节点s
r→next=s;
r=s；//每次新插入的节点就是表尾节点
scanf("%d",&e);//输入e，继续判断
}
r→next=null;//表尾指针域置空
return L;
}
③单链表查找之按序号查找元素
LNode *GetElem_num(LinkList L,int i)//查找第i个位置元素节点
{
if(i==0)
return L;返回头节点
else if(i<0)
return null;
else
{
LNode *s=L→next;
int j=1;
while(s&j④单链表查找之按值查找元素节点
LNode *GetElem_value(LinkList L,Elemtype e)//查找值为e的元素节点
{
LNode *s=L→next;
while(s&s→data!=e) //从第一个节点位置开始，当s非空且s中数据域不是e时，向后找
{
s=s→next;
}
return s;
}
⑤单链表之插入
代码：
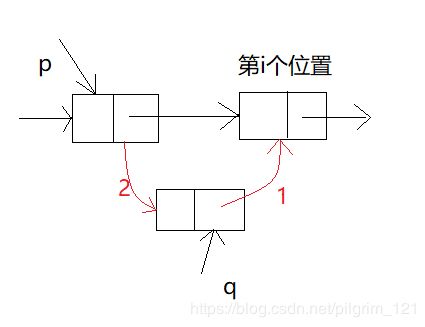
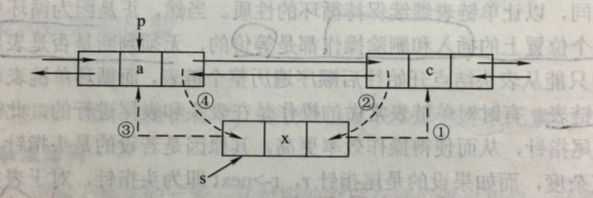
//在第i个位置插入节点q
p=GetElem_num(L,i-1);//找到第i个位置的前驱元素节点p
q→next=p→next;
q→data=x;
p→next=q;
⑥单链表之删除
代码：
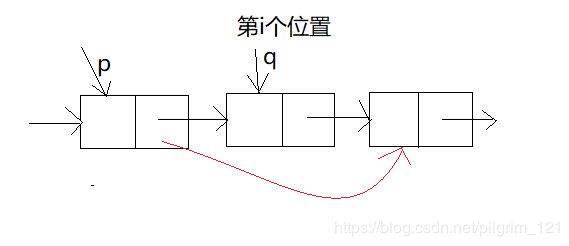
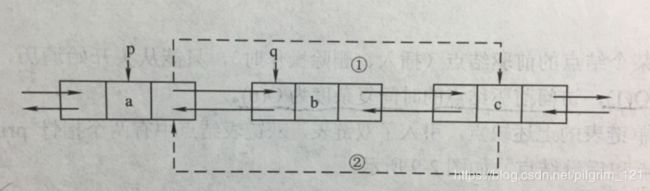
//在第i个位置删除节点q
p=GetElem_num(L,i-1);//找到第i个位置的前驱元素节点p
q=p→next;//找到q
x=q→data;
p→next=q→next;
free(q);//释放q
⑦单链表之求表长
注意： 单链表的表长不包括头节点。
代码：
int lengthList(Linklist L)
{
LNode *p=L→next;
if(p==null)
return 0;
else
int k=0;
while(p)//当p不为空时，数表长
{
k++;
p=p→next;
}
return k;
}
链表之双链表
1.定义
typedef struct DNode{
Elemtype data;
struct DNode *prior,*next;
}DNode,*DLinklist;
2.基本操作
①插入
代码：
s→next=p→next;
p→next→prior=s;
s→prior=p;
p→next=s;
②删除
代码：
q=p→next;
p→next=q→next;
q→next→prior=p;
free(q);
链表之循环链表
1.循环单链表
注意：
a.有尾指针r
b.判空条件为L→next== L
2.循环双链表
注意：判空条件为L→next==L&&L→prior=L
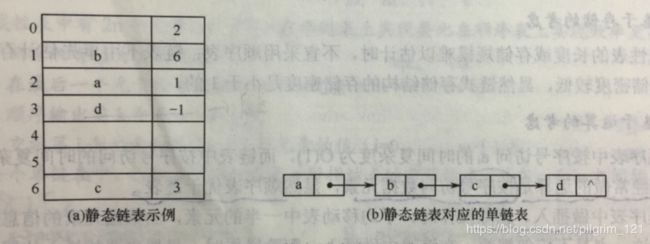
链表之静态链表
1.定义
#define MaxSize 50//最大长度
typedef struct{
Elemtype data;
int next;//下一个元素的下标
}SLinklist[MaxSize];
2.注意
a.结束标志：next=-1;
b.插入，删除时只需要修改指针值
总结
