如何画ROC曲线和FROC曲线

画ROC曲线代码

具体去看https://www.jianshu.com/p/5df19746daf9。，里面的代码讲的详细

例子

# coding=UTF-8
from sklearn import metrics
import matplotlib.pylab as plt

#真实值
GTlist = [1.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 1.0,
          0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0]
#模型预测值
Problist = [0.99, 0.98, 0.97, 0.93, 0.85, 0.80, 0.79, 0.75, 0.70, 0.65,
           0.64, 0.63, 0.55, 0.54, 0.51, 0.49, 0.30, 0.2, 0.1, 0.09]


fpr, tpr, thresholds = metrics.roc_curve(GTlist, Problist, pos_label=1)
roc_auc = metrics.auc(fpr, tpr)  #auc为Roc曲线下的面积
print(roc_auc)


plt.plot(fpr, tpr, 'b',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
# plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([-0.1, 1.1])
plt.ylim([-0.1, 1.1])
plt.xlabel('False Positive Rate') #横坐标是fpr
plt.ylabel('True Positive Rate')  #纵坐标是tpr
plt.title('Receiver operating characteristic example')
plt.show()

 

FROC曲线

FROC曲线介绍

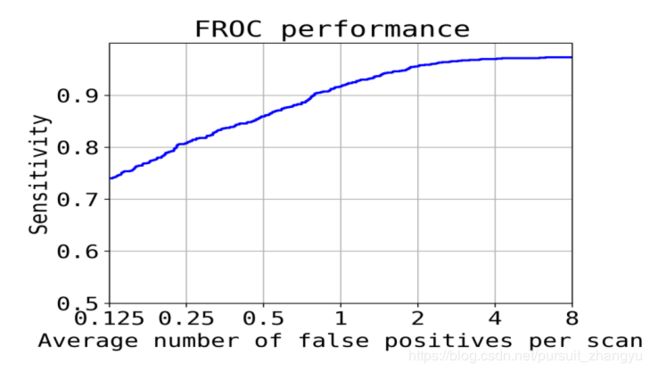
        FROC曲线，是ROC曲线的一个小变种，将横轴上Specificity改为False positives number，即FP数。FROC曲线的横坐标FPS = FP/image_num，image_num代指测试image的个数（如果测试整个luna16的话，那么image_num就是888）。这就是里面会出现0.125,0.25,0.5,1.0,2.0,....,8.0的原因。

       但是得代码中并不是根据横坐标值，然后去得到纵坐标值。如果看过ROC曲线怎么画出来就知道，是通过一个阈值，然后得到sensitive， specificity。FROC也一样，还是得通过阈值，在每个阈值下，就可以求得TP,FP,FN, TN，然后知道sensitive， specificity（公式），然后通过公式FPS = FP/image_num就可以得到。这里面还有一点是luna16的检测指标是CPM值（即在每个样本的假阳例数为1/8，1/4，1/2，1，2，4和8上的平均敏感度）。如果在所有阈值下都没有1/8，1/4，1/2，1，2，4和8。做法很简单直接在这些值附近就可以进行代替。

FROC曲线代码

         首先还是提一下原理吧，sklearn里面没有求FROC曲线的的函数，看了其他代码才知道可以使用求ROC曲线的函数（metrics.roc_curve），使用这个函数就可以完成FROC曲线代码。FROC曲线的纵坐标是sensitity，这个使用metrics.roc_curve这个函数返回值就有（tpr）。FROC曲线的横坐标FP/image_num，image_num代指测试image的个数，这个是知道的，主要是FP，其实FP可以使用fpr得到（metrics.roc_curve的返回值），FPR即False Positive Rate，FPR=FP/(TN+FP)，转化一下FP=FPR(TN+FP),现在都知道了FP，既然所有都知道该怎么求了，就可可以画出FROC曲线。其中TN+FP就是代码里面的(totalNumberOfCandidates - numberOfDetectedLesions)

代码参考的是deeplung的源码

例子

# coding=UTF-8
from sklearn import metrics
import matplotlib.pylab as plt


GTlist = [1.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 1.0,
          0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0,
          0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

Problist = [0.99, 0.98, 0.97, 0.93, 0.85, 0.80, 0.79, 0.75, 0.70, 0.65,
           0.64, 0.63, 0.55, 0.54, 0.51, 0.49, 0.30, 0.2, 0.1, 0.09,
            0.1, 0.5, 0.6, 0.7, 0.8, 0.5, 0.2, 0.3, 0.2, 0.5]

#num of image
totalNumberOfImages = 2
numberOfDetectedLesions = sum(GTlist)
totalNumberOfCandidates = len(Problist)


fpr, tpr, thresholds = metrics.roc_curve(GTlist, Problist, pos_label=1)

#FROC
fps = fpr * (totalNumberOfCandidates - numberOfDetectedLesions) / totalNumberOfImages
sens = tpr

plt.plot(fps, sens, color='b', lw=2)
plt.legend(loc='lower right')
# plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0.125, 8])
plt.ylim([0, 1.1])
plt.xlabel('Average number of false positives per scan') #横坐标是fpr
plt.ylabel('True Positive Rate')  #纵坐标是tpr
plt.title('FROC performence')
plt.show()

下面的代码多了一个平均FROC，供参考

# coding=UTF-8
from sklearn import metrics
import matplotlib.pylab as plt
import numpy as np


GTlist = [1.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 1.0,
          0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0,
          0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

Problist = [0.99, 0.98, 0.97, 0.93, 0.85, 0.80, 0.79, 0.75, 0.70, 0.65,
           0.64, 0.63, 0.55, 0.54, 0.51, 0.49, 0.30, 0.2, 0.1, 0.09,
            0.1, 0.5, 0.6, 0.7, 0.8, 0.5, 0.2, 0.3, 0.2, 0.5]

#num of image
totalNumberOfImages = 2

numberOfDetectedLesions = sum(GTlist)
totalNumberOfCandidates = len(Problist)


fpr, tpr, thresholds = metrics.roc_curve(GTlist, Problist, pos_label=1)


#FROC
fps = fpr * (totalNumberOfCandidates - numberOfDetectedLesions) / totalNumberOfImages
sens = tpr


fps_itp = np.linspace(0.125, 8, num=10001)
sens_itp = np.interp(fps_itp, fps, sens)
frvvlu = 0
nxth = 0.125
for fp, ss in zip(fps_itp, sens_itp):
    if abs(fp - nxth) < 3e-4:
        print(ss)
        frvvlu += ss
        nxth *= 2
    if abs(nxth - 16) < 1e-5: break
print(frvvlu / 7, nxth)

#画图
plt.plot(fps, sens, color='b', lw=2)
plt.legend(loc='lower right')
# plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0.125, 8])
plt.ylim([0, 1.1])
plt.xlabel('Average number of false positives per scan') #横坐标是fpr
plt.ylabel('True Positive Rate')  #纵坐标是tpr
plt.title('FROC performence')
plt.show()

下面是转别人的，原理讲解的很详细，原地址;https://zhuanlan.zhihu.com/p/50750940

1. 二分类的评估标准

其实大家都很容易了解，我就举个例子就过了哈，二分类无非就是一个预测器（随着深度学习流行，大家都只知道model模型了吧？其实在古老的机器学习中，应该叫学习器，预测器等），预测器对输入数据作预测，一般都是预测出该输入数据有多大概率属于正类，因为是二分类嘛，一般设定阈值为0.5（后面细说阈值），大于0.5预测为正，小于则预测为负。

然而你预测的数据是有真实的类别吧，就有可能会出现以下四种情况：

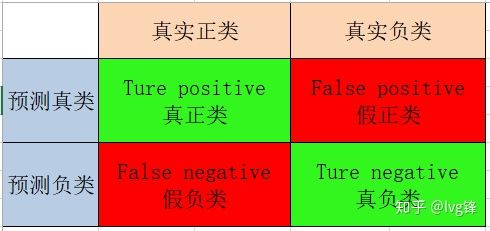
• 正样本被预测为正，当然正确，就是真正类（TP, true positive），真的是正类。
• 正样本被预测为负，错了吧，就是假负类（FN，false negative），假的负类。
• 负样本被预测为正，也是错滴，就是假正类（FP，false positive），假的正类。
• 负样本被预测为负，正确的，就是真负类（TN，true negative），真的是负类。

图1：混淆矩阵（Confusion matrix）

那么要如何评价我们的预测器性能，最简单的就是准确性（Accuracy）：

可是，这样的评估标准真的就很好了吗？其实，是最差滴....

让我们来试着计算一下以下模型的准确率，该模型将 100 个肿瘤分为恶性（正类）或良性（负类）：

图2：准确性的评估标准往往并不客观

数据不均衡的数据集

可以看到，准确率为91%呢，可是这个预测器真的好吗？100个有肿瘤的样本中，91个为良性（90个TN和1个FP），9个为恶性（1个TP和8个FN）。

在 91 个良性肿瘤中，该模型将 90 个正确识别为良性。这很好。不过，在 9 个恶性肿瘤中，该模型仅将 1 个正确识别为恶性。这是多么可怕的结果！9 个恶性肿瘤中有 8 个未被诊断出来！

虽然 91% 的准确率可能乍一看还不错，但如果另一个肿瘤分类器模型总是预测良性，那么这个模型使用我们的样本进行预测也会实现相同的准确率（100 个中有 91 个预测正确）。换言之，我们的模型与那些没有预测能力来区分恶性肿瘤和良性肿瘤的模型差不多。

当使用分类不平衡的数据集（比如正类别标签和负类别标签的数量之间存在明显差异）时，单单准确率一项并不能反映全面情况。这时候就需要查准率和查全率。

2. 查准率和查全率

现实情况复杂，针对预测器需求的不同，例如：信息检索中，都有以下情况（下面有点绕）：

• • 查准率：预测器检索出的信息要尽可能的满足用户（即，预测感兴趣（正类）要更准，减少预测出用户不感兴趣的信息数（假正类的数量））
  • 查全率：用户感兴趣的信息要尽可能检索出来（即，用户感兴趣的信息要预测全，减少预测为不感兴趣的信息而实际确实感兴趣信息的数量（假负类））

上述的无非就是查准率（Precision）和查全率（Recall）：

同样举例子：0,1,2,...,9，十个信息，用户对于0-4的5个信息是不感兴趣的，而5-9的信息是感兴趣的。以下两个预测器A和B：

• 预测器A预测：0-5是用户不感兴趣的，6-9是用户感兴趣的。
  • 查准率：100%，查全率：75%
• 预测器B预测：0-3是用户不感兴趣的，4-9是用户感兴趣的。
  • 查准率：80%，查全率：100%

选择哪个预测器更好？这时候就需要看需求了，是要高的查准率还是高的查全率？

但是，更多的情况是预测器间差距小，想要一个更好的预测器，如何评估？

可以使用F1-Score来评估：

上述例子中，预测器A的F1-Score为0.857，预测器B的F1-Score为0.889。

当然上述的例子有点极端，但是真实计算过程大概就那样！

3. ROC曲线和AUC的计算

在真实的预测器中，要想调整查准率和查全率是很简单的，还记得我们第一节说的阈值。

这里好好说下这个概念，预测器实际是预测出输入样本属于正类别的概率，而我们上述所说的预测正类，全是因为设置了阈值，一般设置为0.5。

通过改变阈值的设置，可以改变预测器的准确率，查准率，查全率等。那么要对一个分类器作全面的评估，我们使用ROC曲线（Receiver operating characteristic）。

参考资料：维基百科：ROC曲线

有人可能会问：为啥要用不同阈值评估，不可以统一设置阈值为0.5，大家都来比较准确率，查准率和查全率就得了，不用那么麻烦。
这是因为，只评估单一阈值，是对分类器不公平的，不同分类器可能会对不同阈值有一定的依赖，在这一阈值下可能A分类性能都要好，但在另一个阈值下，可能B分类性能要更好些。所以要做到更加客观的评估，我们绘出ROC曲线。

那么ROC曲线是如何通过不同阈值来计算出最终结果的呢？

ROC曲线实际上就是一个 的坐标空间，坐标上的每一个点都是特定阈值下的（1-specificity，sensitivity）。

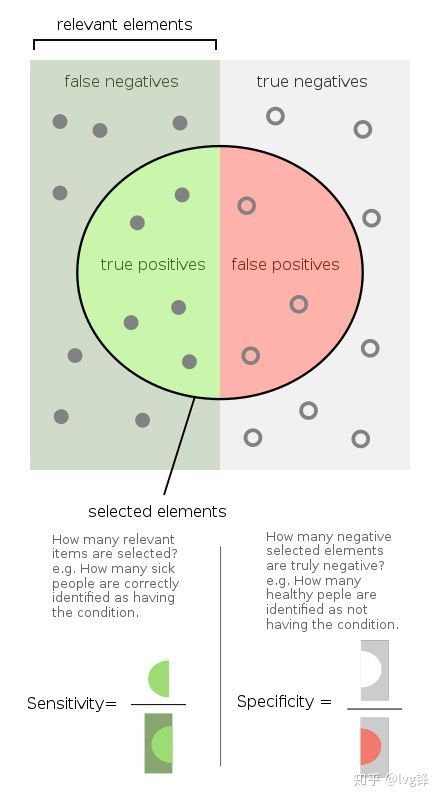
图3：灵敏度和特异度

又来两个名词了，有点混：

从公式上就可以看出，其实灵敏度(Sensitivity)就是上述提到的查全率，特异度(Specificity)实际含义是：预测的正类中，实际上是负类的个数占所有实际负类的比例。

至于为啥用这两个作为坐标点绘出ROC曲线，我也不得而知，其实还有一条名为P-R曲线是根据查准率和查全率绘出的，这里不做细说。

那么知道了坐标点是（1-specificity，sensitivity,），阈值又是如何选取的呢？

其实很简单，就是所有预测概率的集合，按从高到低排列。

这里举一个例子就很明白了。

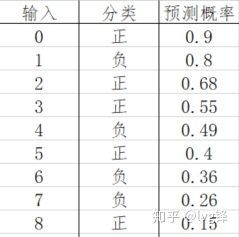
图4：预测器A对样本集（9个）的预测结果及其真实类别

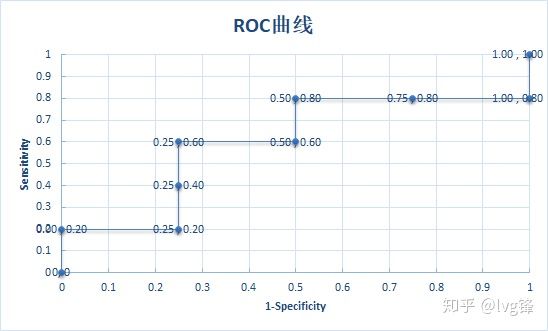
从高到低，首先阈值第一个点设定可能是1.0，即所有预测结果都是负类，显然，这时候坐标点就是（0，0），然后阈值=0.9，即大于等于0.9的才是正类，上图就只有一个正类，那么此时sensitivity=1/5,1-specificity=0/4，以此类推，最后画成下图：

图5：ROC曲线

显然，当ROC曲线阈值集合越大，曲线就会越平滑（这里例子少，一点都不平滑，但是给大家看明白计算过程就好了。）

那么要评估预测器间的好坏，就可以通过ROC曲线来评估了。

如何评估？我们使用AUC（Area under curve）值计算，英文就很明白了吧，曲线下的面积，显然面积极限值就是1。谁的面积大，谁的预测结果好！

使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

AUC的含义是什么呢？我也不知道，找到以下引文：

The AUC value is equivalent to the probability that a randomly chosen positive example is ranked higher than a randomly chosen negative example.
首先AUC值是一个概率值，当你随机挑选一个正样本以及一个负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然，AUC值越大，当前的分类算法越有可能将正样本排在负样本前面，即能够更好的分类。

ROC曲线能被业界经常选用（Camelyon16就是用的这个吧），因为它有一个很好的特性：

当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。

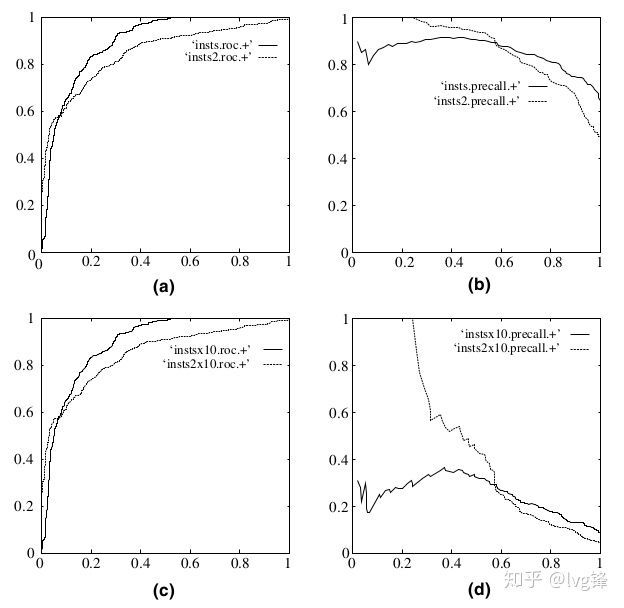
图6：(a)和(c)是ROC曲线，(b)和(d)是P-R曲线。(a,b)展示了测试集数据正负样本分布均衡的结果；(c,d)展示了测试集数据正负样本分布不均衡(1:10)的结果;

4. FROC曲线

FROC（Free-Response ROC）曲线搞了我好久，实在没明白，后面细查才发现这是一篇论文提出的：Operating characteristics, signal delectability, and the methods of free response，1978年提出的一个评估方案。也已经被业界广泛引用了，起码LUNA的比赛，Camelyon16的比赛都在用这个。

我实在懒得看一篇冗长的论文（懒呀！），最后难得找到了一个定义：

FROC(Free-response ROC)曲线

经典的ROC方法不能解决对一幅图像上多个异常进行评价的实际问题，70年代提出了无限制ROC的概念(free-response ROC;FROC)。FROC允许对每幅图像上的任意异常进行评价。

嗯，可能用的少？没什么像ROC曲线那么详尽的解释，但是既然有，我们就了解了解它是如何计算的就好了！（用多了可能就明白了，我也是刚刚明白而已....）

其实简单来说就一句话，FROC曲线，是ROC曲线的一个小变种，将横轴上1-Specificity改为False positives number，即FP数。可是问题来了？向Camelyon16中给出的评估指标，0.25,0.5,0.75,1.0,2.0,....,8.0又是什么回事？不是说好的FP数吗？怎么会出现小数呢？再说FP可能很多呢？怎么尽头才是8.0？

嗯...大家好好理解下引用那段话：ROC无法解决一幅图像上多个异常的现象。其实我们思维固定了，FROC针对的问题是一张图上可能出现多个问题的情况，而不是常见的二分类，一张图预测只有一个正或负，要么对或错。

它针对的问题也恰恰是类似Camelyon16的问题，我以Camelyon16来举例。

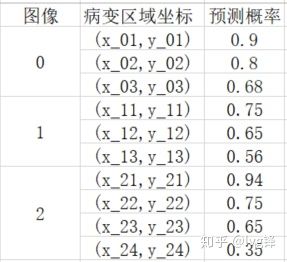
Camelyon16的Lesion-based评估标准上，要做的是评估你预测有转移癌的病变区域是否正确。很明显一张切片上有可能有多个病变区域，也就符合上述说法了。这里的FROC中横轴的FP数其实是FPs per image。所以也就会出现小数的情况了。

图7：简单的样例

还记得Camelyon16学习记录(1)：这个比赛究竟是啥？提到的，如果病变区域坐标的正负，其实就看它是否在真实病变区域的一定范围内，如果是就是正，不是就是负。

那么FROC的画图就很简单了，同理ROC曲线，阈值按预测概率从高到低分别设定。每个阈值都可以得到总的FP的数量，FPs per image=FPs/image_num。所以小数的出现就合理了吧。