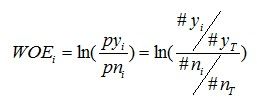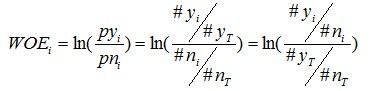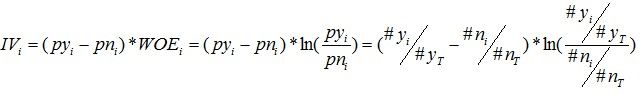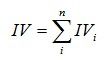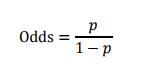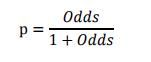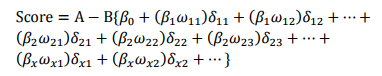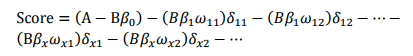评分卡建模流程

基于Logistic回归的申请评分卡模型开发

基本申请评分卡建模流程：

1.数据准备：收集并整合在库客户的数据，定义目标变量，排除特定样本。

2.探索性数据分析：评估每个变量的值分布情况，处理异常值和缺失值。

3.数据预处理：变量筛选，变量分箱，WOE转换、样本抽样。

4.模型开发：逻辑回归拟合模型。

5.模型评估：常见几种评估方法，ROC、KS等。

6.生成评分卡

1. 数据准备

因为不同评级模型所需要的数据也是不同的，所以在开发信用评级模型之前，要先明确我们需要解决的问题。

1.1 排除一些特定的建模客户

用于建模的客户或者申请者必须是日常审批过程中接触到的，需要排除异常情况。如 欺诈，特殊客户。

1.2 明确客户属性

根据不同的数据来源，可以分为以下几类：

1.人口统计特征：客户的基本特征，如性别，年龄、居住情况、年收入等

2.征信机构数据和外部评分:如人行征信报告、芝麻分等。

3.其他数据来源。

1.3 目标变量的确立

预测模型的一个基本原理是用历史数据来预测未来，申请者评分模型需要解决的问题是未来一段时间（如12个月）客户出现违约（如至少一次90天或90天以上逾期）的概率。先将客户标签定义为二分类，不良/逾期：观察窗口内，观察窗口内，60/90/120天算逾期日期；良好:从未或截止逾期；从未或在观察期内截止逾期

其中关于不良/逾期需要界定以下两项内容：确定违约日期时长、观察窗口期设置。

定违约日期时长

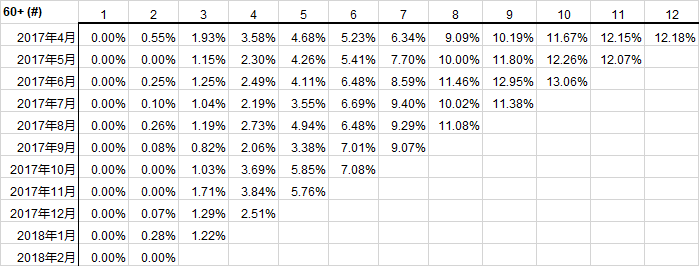
违约时长的确定可以使用逾期转移矩阵来确定

(以上数据纯属虚构)

通过上图可以看出来，M3客户变坏的概率为93%.也就是说当客户逾期超过60天后，被催回的几率为7%。因此，可以定义逾期超过60天的客户为坏客户。

违约窗口期设置——账龄分析

一般情况下巴塞尔协议硬性要求12个月及以上作为窗口期。一般情况下，观察窗口=3-5倍的预测窗口，同时决定信用评等模型开发所需数据期间长度，一般又会从最新资料的留存时点开始推算，利用账龄分析观察目标客户的违约成熟期长度，借此设定观察期长度（预测窗口的时间长度）。比如2017.04开卡的人，第10个月，稳定成熟了，观察窗口时间可以确定为10-12个月；2017.05开卡的人，第11个月，稳定成熟了，观察窗口时间可以确定为11-12个月。

好坏客户标签

通过观察转移矩阵和账龄，我们定义在10-12月逾期超过60天的客户为坏客户。同时第十个月没有发生逾期的客户定义为好客户。那逾期天数在0-60之间的客户怎么定义呢，，比如45天，这样的客户不能简单的将其归为好客户或坏客户，需要暂时将他从模型样本中摘除，将其定义为不确定的客户。

2.数据描述和探索性数据分析

数据准备和数据预处理阶段消耗大量的时间，主要的工作包括数据获取、探索性数据分析、缺失值处理、数据校准、数据抽样、数据转换、离散变量降维、连续变量优先分段等工作。

EDA实施包含以下过程：

描述性统计。

评估每个变量值的分布并检验正态假设

极端值的识别和处理

缺失值的计算和处理

2.1 描述性统计

描述性统计是使用一些统计量来对变量分析，如：平均值，中位数，总数，标准差等等。

2.2 变量值分布

直方图用于绘制联系变量的分布，饼图或条形图用于名义变量和顺序变量。

2.3 极端值识别和处理

极端值的识别方法基于不同的应用，有多种选择。这里大概提两个识别方法：

1）每个变量设定一个正常取值的范围，在简单的统计指标基础上进行验证。比如：连续值设定均值+-3倍标准差。名义变量和顺序变量，总体的1%或更多视为正常。

2）用聚类算法将数据分为较小的子集，只包含较少数量观测值的簇，认定为极端值。

一般极端值处理的方法：值替换。

另外，如果极端值超过10%，表明生成数据的机制不止1个。要调查是否需要针对每个群单独开发模型。

2.4 缺失值处理

1）.直接剔除

2）.根据样本之间的相似性填补（统计替换）

3）.根据变量之间的相关性填补（拟合）

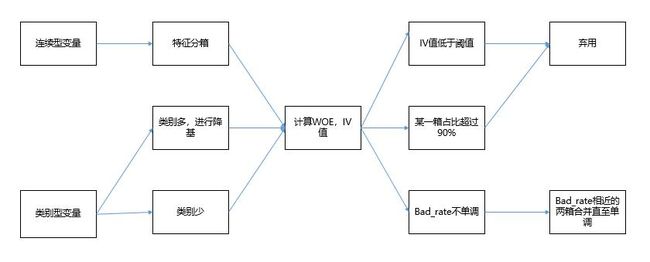
3.数据预处理

3.1变量筛选

在数据准备的过程中，我们将所有能收集到的特征都整合到数据集中。但在建模的时候，并非所有的特征都能用到模型上，因此，在收集的所有特征中筛选出对违约状态影响最大的特征，作为入模特征来开发模型。

筛选方法主要有：逐步选择法， 随机森林筛选变量，IV值筛选

1）逐步选择法；基于参数估计的卡方显著性来决定那些变量将被保留在模型中。保证最终模型中的所有变量都是显著的。

2）机器学习方法：使用随机森林，gbdt，xgboost等方法输出变量重要性排序来选择变量。

3）IV值筛选：选择IV值高的变量做为备选变量。

IV（Information Value）：信息价值

IV 可以用来衡量自变量的预测能力。

为了介绍IV的计算方法，我们首先需要认识和理解另一个概念——WOE

WOE的全称是“Weight of Evidence”，即证据权重。WOE是对原始自变量的一种编码形式。

要对一个变量进行WOE编码，需要首先把这个变量进行分组处理。分组后，对于第i组，WOE的计算公式如下：

其中，pyi是这个组中响应客户（风险模型中，对应的是违约客户，总之，指的是模型中预测变量取值为“是”或者说1的个体）占所有样本中所有响应客户的比例，pni是这个组中未响应客户占样本中所有未响应客户的比例，#yi是这个组中响应客户的数量，#ni是这个组中未响应客户的数量，#yT是样本中所有响应客户的数量，#nT是样本中所有未响应客户的数量。

从这个公式中我们可以体会到，WOE表示的实际上是“当前分组中响应客户占所有响应客户的比例”和“当前分组中没有响应的客户占所有没有响应的客户的比例”的差异。

对这个公式做一个简单变换，可以得到：

变换以后我们可以看出，WOE也可以这么理解，他表示的是当前这个组中响应的客户和未响应客户的比值，和所有样本中这个比值的差异。这个差异是用这两个比值的比值，再取对数来表示的。WOE越大，这种差异越大，这个分组里的样本响应的可能性就越大，WOE越小，差异越小，这个分组里的样本响应的可能性就越小。

对于分组i，也会有一个对应的IV值，计算公式如下：

有了一个变量各分组的IV值，我们就可以计算整个变量的IV值，方法很简单，就是把各分组的IV相加：

其中，n为变量分组个数。

3.2变量处理

在进行变量筛选后，我们就得到了可用作信用风险评级模型开发的样本总体。在数据预处理阶段，有三个任务对于评分卡开发十分关键：

1）抽样和权重计算

2）通过将某些类别和并降低名义变量的基数，将连续变量分箱。

3）证据权重转换（WOE）

3.2.1样本抽样

为了验证评级模型的区分能力及预测准确性，通常会将样本分为训练集和测试集，这种方法叫样本抽样。

3.2.2 降低基数

当名义变量的类别数量过多时，需要降低其基数。

一般有以下几种策略：

1.将相同含义的变量合并

2.出现频率小的类别合并为一个新的类别。

3.合并变量的类别使得预测指标最大化。

3.2.3 连续变量分箱

连续变量的分段方法通常分为等距分箱、等频分箱、最优分箱。等距分段是指将连续变量分为等距离的若干区间。最优分段是指根据变量的分布属性，并结合该变量对违约状态变量预测能力的变化，按照一定的规则将属性接近的数值聚在一起，形成距离不相等的若干区间，最终得到对违约状态变量预测能力最强的最优分段。

等距分箱 

　　 从min到max之间,均分为 N 等份, 这样, 如果 A,B 为最小最大值, 则 每个区间的长度为 W=(B−A)/N  , 区间边界值为A+W,A+2W,….A+(N−1)W 。这里只考虑边界，每个等份里面的实例数量可能不等。 

　　  等频分箱 

　　 区间的边界值要经过选择, 使得每个区间包含大致相等的实例数量 。比如说 N=10 ,每个区间应该包含大约10%的实例。 

最优分箱

根据变量的分布属性，并结合该变量对违约状态变量预测能力的变化，按照一定的规则将属性接近的数值聚在一起，形成距离不相等的若干区间，最终得到对违约状态变量预测能力最强的最优分段。

 

3.2.4 WOE转换

WOE转换可以将逻辑回归模型变为标准评分卡格式，当然不使用WOE转换也是能建立标准评分卡。

WOE转换其实很简单，就是对筛选出来并且已经完成分组的变量，使用计算出来的每组的WOE值替换变量取值。

需要注意的是，对于不同的变量类型有点不同的要求。对于类别型变量，因为类别型变量之间不存在任何序列关系，所以不同类型的WOE值可以任意排序。然而，对于连续变量，WOE值必须按照分组的自然序列排序，以保持连续原始变量中所包含的顺序关系。

4.模型开发

经过数据准备与处理阶段，目前我们手上已经有了筛选出来，并完成WOE替换的自变量，以及完成好坏定义的因变量。接下来的工作，就是将自变量和因变量放入模型进行拟合。

python中可以用sklearn中的LogisticRegression 或者statsmodels中的Logit 进行拟合。 sas可以用proc logistic 进行拟合。

5.模型评估

模型拟合之后，需要评估模型的好坏。好的模型一般要有以下三个基本要求：

1.精确性。模型在预测时，要有一定的精确性。

2.稳健性。模型必须对从总体样本中抽取的所有样本都有效。

3.有意义

精确性有以下几个评估方法：

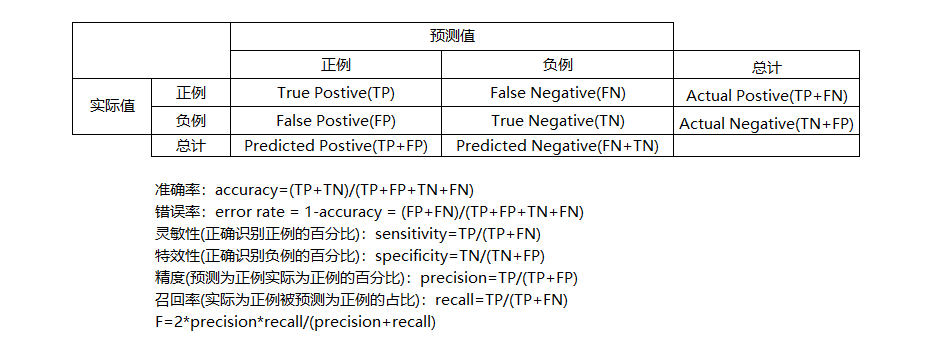
1）混淆矩阵

逻辑回归也是分类模型，先定义违约客户为正例，正常客户为负例。并且定义概率的临界值为0.5，则概率大于或等于临界值为违约即正例，可以计算出违约与正常分类准确和错误的数量。

对于一般的二分类模型来说，准确率和错误率就能体现模型的好坏。但对于类别不均衡问题，比如逾期率为1%的样本，我们要的正例，也就是逾期客户只有1%。这时候，准确率就存在误差。为此，可以使用灵敏性（召回率），特效性，精度，F来度量模型的好坏。

对于一个评分卡模型，将好客户预测为坏客户的损失要比将坏客户预测为好客户的损失要少，因此更加注重的是召回率。

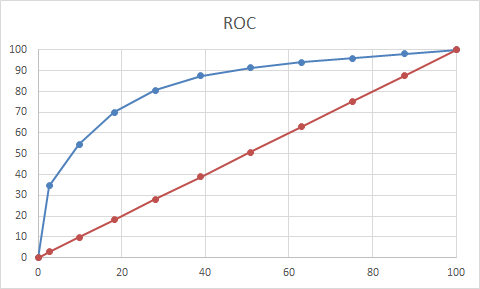
2）ROC曲线：

接受者操作特征（Receiver Operating Characteristic）曲线是一种比较两个分类模型有用的可视化工具。ROC曲线显示了给定模型的真正例率(TPR)和假正例率(FPR)之间的权衡,TPR = TP/(TP+FN) = sensitivity，FPR=FP/(TN+FP)=1-specificity。因此， ROC 曲线也可以理解为不同阈值下Sensitivity和1-Specificity的轨迹。

图中，ROC曲线以下的面积就是模型准确率的度量（AUC）。

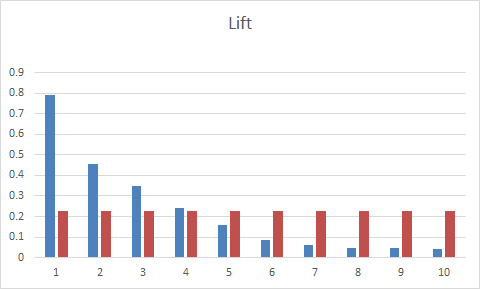
3）lift(提升指数):

它衡量的是，与不利用模型相比，模型的预测能力“变好”了多少。不利用模型，我们只能利用“正例的比例是TP+FN/(TP+FN+TN+FP)”这个样本信息来估计正例的比例（baseline model），而利用模型之后，我们不需要从整个样本中来挑选正例，只需要从我们预测为正例的那个样本的子集(TP+FN)中挑选正例，这时预测的准确率为TP/(TP+FN)。

Lift 图是不同阈值下Lift和Depth的轨迹

Lift =(TP/(TP+FN))/(TP+FN/(TP+FN+TN+FP))

Depth=(TP+FP)/ (TP+FN+TN+FP) ,可以理解为预测成正例的比例

蓝色为利用模型后的结果，红色为不利用模型的结果。

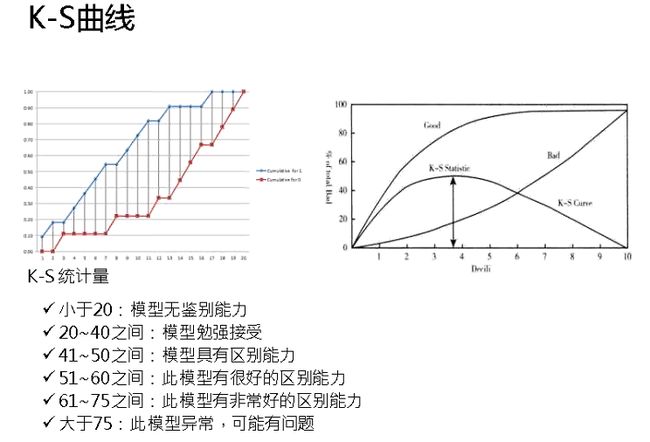
4）KS(Kolmogorov-Smirnov)：

指标衡量的是好坏样本累计分部之间的差值。 

好坏样本累计差异越大，KS指标越大，那么模型的风险区分能力越强。

 计算每个区间的累计好账户数占总好账户数比率(good%)和累计坏账户数占总坏账户数比率(bad%)。 取最大值即得此评分卡的K-S值。

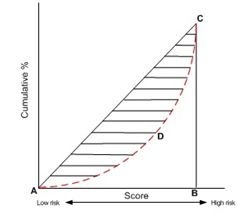
5）GINI系数:

GINI统计值衡量坏账户数在好账户数上的的累积分布与随机分布曲线之间的面积，好账户与坏账户分布之间的差异越大，GINI指标越高，表明模型的风险区分能力越强。计算每个区间的累计好账户数占总好账户数比率（累计good%）和累计坏账户数占总坏账户数比率(累计bad%)。  按照累计好账户占比和累计坏账户占比得出下图所示曲线ADC。 计算出图中阴影部分面积，阴影面积占直角三角形ABC面积的百分比，即为GINI系数。

6.生成评分卡

由逻辑回归的基本原理，我们将客户违约的概率定为p，则正常的概率为1-p。可以得到：

此时，客户违约的概率p可表示为：

           Odds被称为优势比，logit函数仅仅是比例的自然对数。而logistic回归模型是用比例的自然对数作为因变量的线性回归模型。

评分卡设定的分值刻度可以通过将分值表示为比率对数的线性表达式来定义，即可表示为下式：

其中，A和B是常数。

            式中的负号可以使得违约概率越高，得分越低。通常情况下，这是分值的理想变动方向，即高分值代表低风险，低分值代表高风险。   

            式中的常数A、B的值可以通过将两个已知或假设的分值带入计算得到。通常情况下，需要设定两个假设： 

            （1）给某个特定的比率设定特定的预期分值； 

            （2）确定比率翻番的分数（PDO） 

            根据以上的分析，我们首先假设比率为x的特定点的分值为P。则比率为2x的点的分值应该为P+PDO。代入式中，可以得到如下两个等式： 

            假设 设定评分卡刻度使得比率为{1:20}（违约正常比）时的分值为50分，PDO为10分，代入式中求得：B=14.43，A=6.78 

则分值的计算公式可表示为： 

            评分卡刻度参数A和B确定以后，就可以计算比率和违约概率，以及对应的分值了。通常将常数A称为补偿，常数B称为刻度。 

            则评分卡的分值可表达为： 

            式中：变量x1…xn是出现在最终模型中的自变量，即为入模指标。由于此时所有变量都用WOE转换进行了转换，可以将这些自变量中的每一个都写(βiωij)δij的形式： 

 

            式中ωij 为第i行第j个变量的WOE，为已知变量；βi为逻辑回归方程中的系数，为已知变量；δij为二元变量，表示变量i是否取第j个值。上式可重新表示为： 

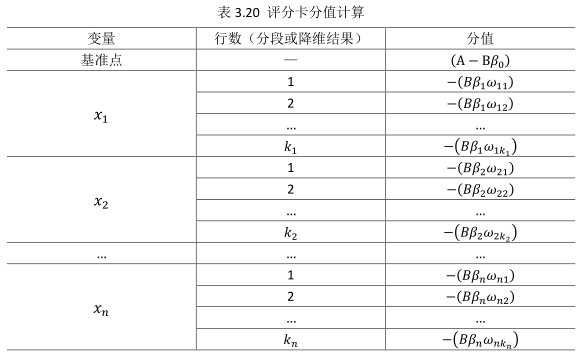
            此式即为最终评分卡公式。如果x1…xn变量取不同行并计算其WOE值，式中表示的标准评分卡格式，如表3.20所示： 

表3.20表明，变量x1有k1行，变量x2有k2行，以此类推；基础分值等于(A−Bβ0)；由于分值分配公式中的负号，模型参数β0，β1，…，βn也应该是负值；变量xi的第j行的分值取决于以下三个数值： 

（1）刻度因子B； 

（2）逻辑回归方程的参数βi； 

（3）该行的WOE值，ωij