Huffman编码解码
Huffman编码解码
霍夫曼(Huffman)编码问题也就是最优编码问题,通过比较权值逐步构建一颗Huffman树,再由Huffman树进行编码、解码。
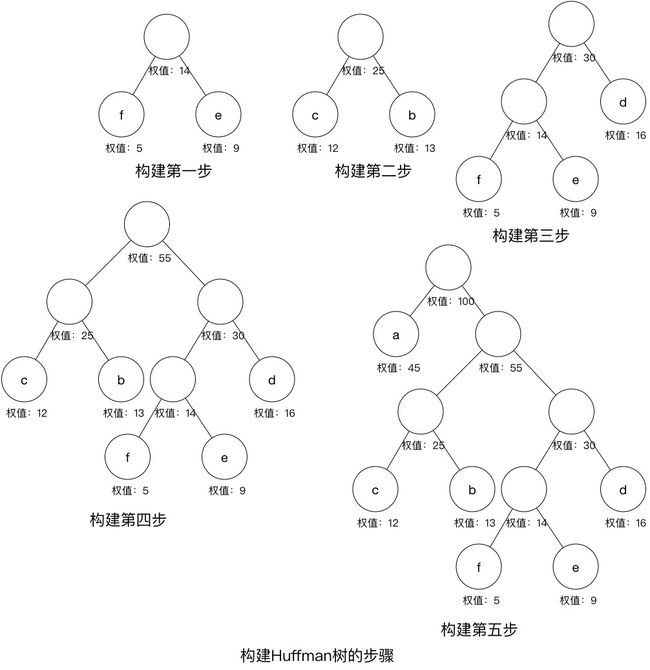
其步骤是先构建一个包含所有节点的线性表,每次选取最小权值的两个节点,生成一个父亲节点,该父亲节点的权值等于两节点权值之和,然后将该父亲节点加入到该线性表中,再重复上述步骤,直至构成一个二叉树,注意已经使用过的节点不参与。
Huffman编码贪心原理
编码原理
把每个字符看作一个单节点子树放在一个树集合中,每棵子树的权值等于相应字符的频率。每次取权值最小的两棵子树合成一棵新树,并重新放到集合中。新树的权值等于两棵子树权值之和。
贪心选择性
设 x 和 y 是频率最小的两个字符,则存在前缀码使得 x 和 y 具有相同码长,且仅有最后一位编码不同。换句话说,贪心选择保留了最优解。
优化子结构
设 T 是加权字符集 C 的最优编码树, x 和 y 是树 T 中两个叶子,且互为兄弟结点, z 是它们的父结点。若把 z 看成具有频率 f(z)=f(x)+f(y) 的字符,则树 T′=T−{x,y} 是字符集 C′=C−{x,y}⋃{z} 的一棵最优编码树。换句话说,原问题的最优解包含子问题的最优解。
举例说明
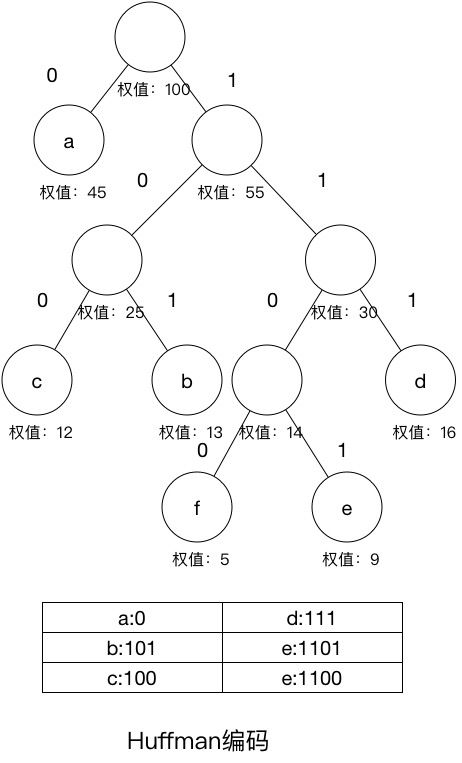
编码表
| 字符 | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 频率 | 45 | 13 | 12 | 16 | 9 | 5 |
| 编码 | 0 | 101 | 100 | 111 | 1101 | 1100 |
下面将解释为什么是这样编码,在解释之前先说明一个概念:
- 前缀码:任何一个编码都不是另一个编码的前缀(prefix)。
如果Huffman编码符合前缀码的要求的话,那么绝不会出现编码二义性的问题。而且通过权值这一参考量,构成了最优编码。
原理图
Huffman编码解码算法实现
节点信息结构
// 节点信息结构
struct Node {
// 值
string value;
// 权值
float weight;
// 父节点
int parent;
// 左子节点
int lchild;
// 右子节点
int rchild;
};编码信息结构
// 编码信息结构
struct Code {
// 编码字符
int bit[maxBit];
// 开始位置
int start;
// 值
string value;
};全局常量和全局变量
const int INF = 1000000000;
const int maxBit = 1 << 5;
const int maxNode = 1 << 10;
const int maxCode = 1 << 10;
// 节点数组
Node huffman[maxNode];
// 编码数组
Code huffmanCode[maxCode];
// n个字符串
int n;初始化Huffman树
// 初始化Huffman树
void initHuffmanTree() {
for(int i = 0; i < (2 * n) - 1; i++) {
huffman[i].weight = 0;
huffman[i].value = "";
huffman[i].parent = -1;
huffman[i].lchild = -1;
huffman[i].rchild = -1;
}
}构造Huffman树
// 贪心法
// 构造Huffman树
void huffmanTree() {
// 循环构建Huffman树
for(int i = 0; i < n - 1; i++) {
// m1,m2存放所有节点中权值最小的两个节点权值
int m1 = INF;
int m2 = INF;
// x1,x2存放所有节点中权值最小的两个节点下标
int x1 = 0;
int x2 = 0;
for(int j = 0; j < n + i; j++) {
if(huffman[j].weight < m1 && huffman[j].parent == -1) {
m2 = m1;
x2 = x1;
m1 = huffman[j].weight;
x1 = j;
} else if(huffman[j].weight < m2 && huffman[j].parent == -1) {
m2 = huffman[j].weight;
x2 = j;
}
}
// 设置找到的两个节点的x1,x2的父节点信息
huffman[x1].parent = n + i;
huffman[x2].parent = n + i;
huffman[n + i].weight = huffman[x1].weight + huffman[x2].weight;
huffman[n + i].lchild = x1;
huffman[n + i].rchild = x2;
}
}Huffman编码
// huffman编码
void huffmanEncoding() {
// 临时结构
Code cd;
int child, parent;
for(int i = 0; i < n; i++) {
cd.value = huffman[i].value;
cd.start = n - 1;
child = i;
parent = huffman[child].parent;
// 未到根节点
while(parent != -1) {
// 左孩子
if(huffman[parent].lchild == child) {
cd.bit[cd.start] = 0;
} else {
// 右孩子
cd.bit[cd.start] = 1;
}
cd.start--;
// 设置下一循环条件
child = parent;
parent = huffman[child].parent;
}
// 保存求出的每个叶子节点的Huffman编码结构
for(int j = cd.start + 1; j < n; j++) {
huffmanCode[i].bit[j] = cd.bit[j];
}
huffmanCode[i].start = cd.start;
huffmanCode[i].value = cd.value;
}
}打印Huffman编码信息
// 打印每个叶节点的Huffman编码和编码起始值
void printHuffmanCode() {
for(int i = 0; i < n; i++) {
cout << "第" << i + 1 << "个字符 " << huffmanCode[i].value << " 的Huffman编码为:";
for(int j = huffmanCode[i].start + 1; j < n; j++) {
cout << huffmanCode[i].bit[j];
}
cout << " 编码起始值为:" << huffmanCode[i].start << endl;
}
cout << endl;
}解码Huffman编码
// 解码Huffman编码
void HuffmanDecoding(string s) {
vector<string> v;
// 标识位
int ok = 1;
for(int i = 0; i < s.length();) {
// 根节点
int x = (2 * n) - 1 - 1;
// 不为叶子节点
while(huffman[x].lchild != -1 && huffman[x].rchild != -1) {
// 左子树
if(s[i] == '0') {
x = huffman[x].lchild;
} else {
// 右子树
x = huffman[x].rchild;
}
i++;
// 处理0,1序列有误
// 这种情况一般是结尾0,1序列少了,导致最后一个字符串解码失败
if(i == s.length() && huffman[x].lchild != -1) {
ok = 0;
break;
}
}
if(ok) {
v.push_back(huffman[x].value);
}
}
if(ok) {
for(int i = 0; i < v.size(); i++) {
cout << v[i];
}
cout << endl << endl;
} else {
cout << "解码有误。" << endl << endl;
}
}主函数
int main() {
while(true) {
// 初始化
// 输入数据
cout << "请输入字符串个数(0退出):";
cin >> n;
if(!n) {
break;
}
// 初始化Huffman树
initHuffmanTree();
for(int i = 0; i < n; i++) {
cout << "一共" << n << "个字符串,请输入第" << i + 1 << "个字符串及其权值:";
cin >> huffman[i].value;
cin >> huffman[i].weight;
}
// 构造Huffman树
huffmanTree();
// huffman编码
huffmanEncoding();
// 打印每个叶节点的Huffman编码和编码起始值
printHuffmanCode();
while(true) {
cout << "请输入一段符合上述编码的0,1序列(q进入下一次编码解码):";
string s;
cin >> s;
if(s[0] == 'q') {
cout << endl;
break;
}
cout << "原始0,1序列为:" << s << endl;
cout << "解码后为:";
// 解码
HuffmanDecoding(s);
}
}
return 0;
}测试主程序
#include 输出数据
请输入字符串个数(0退出):6
一共6个字符串,请输入第1个字符串及其权值:a 45
一共6个字符串,请输入第2个字符串及其权值:b 13
一共6个字符串,请输入第3个字符串及其权值:c 12
一共6个字符串,请输入第4个字符串及其权值:d 16
一共6个字符串,请输入第5个字符串及其权值:e 9
一共6个字符串,请输入第6个字符串及其权值:f 5
第1个字符 a 的Huffman编码为:0 编码起始值为:4
第2个字符 b 的Huffman编码为:101 编码起始值为:2
第3个字符 c 的Huffman编码为:100 编码起始值为:2
第4个字符 d 的Huffman编码为:111 编码起始值为:2
第5个字符 e 的Huffman编码为:1101 编码起始值为:1
第6个字符 f 的Huffman编码为:1100 编码起始值为:1
请输入一段符合上述编码的0,1序列(q进入下一次编码解码):010011110111011100
原始0,1序列为:010011110111011100
解码后为:acdbef
请输入一段符合上述编码的0,1序列(q进入下一次编码解码):00010010110010111011101110011001111110101
原始0,1序列为:00010010110010111011101110011001111110101
解码后为:aaacbcbeeffddab
请输入一段符合上述编码的0,1序列(q进入下一次编码解码):010110011
原始0,1序列为:010110011
解码后为:解码有误。
请输入一段符合上述编码的0,1序列(q进入下一次编码解码):q
请输入字符串个数(0退出):0
Process returned 0 (0x0) execution time : 16.174 s
Press any key to continue.