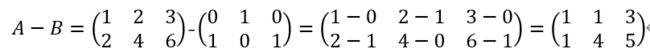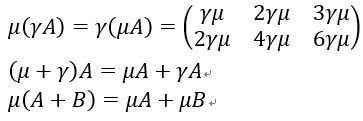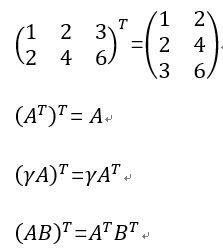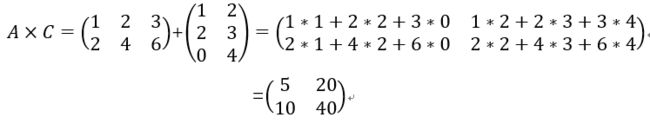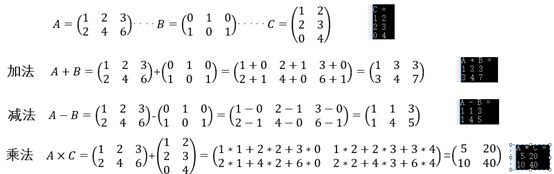Qt开发笔记之线性代数：线性代数矩阵以及Eigen库的介绍、编译和使用

若该文为原创文章，未经允许不得转载
原博主博客地址：https://blog.csdn.net/qq21497936
原博主博客导航：https://blog.csdn.net/qq21497936/article/details/102478062
本文章博客地址：https://blog.csdn.net/qq21497936/article/details/84339214
各位读者，知识无穷而人力有穷，要么改需求，要么找专业人士，要么自己研究

红胖子(红模仿)的博文大全：开发技术集合（包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软硬结合等等）持续更新中…（点击传送门）

Qt开发专栏：三方库开发技术

 

前话

       研究Fec算法，需要使用到矩阵基本知识，主要包括加法、减法和乘法，先重温矩阵知识，然后使用开源库Eigen进行矩阵计算，包括编译、配置和使用。

 

线性代数之矩阵以及基本运算

    （注意：当先FEC算法中用到的主要是加法、减法和乘法）

简介

       矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中：

1. 在物理学中，矩阵于电路学、力学、光学和量子物理中都有应用；
2. 计算机科学中，三维动画制作、图像识别和一些算法也需要用到矩阵；

      矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。对一些应用广泛而形式特殊的矩阵，例如稀疏矩阵和准对角矩阵，有特定的快速运算算法。关于矩阵相关理论的发展和应用，请参考矩阵理论。在天体物理、量子力学等领域，也会出现无穷维的矩阵，是矩阵的一种推广。

定义

      由m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：

      

        这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。

        元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。

基本运算：加法、减法、数乘、转置、共轭、共轭转置

        先定义矩阵A、B、C三个矩阵，如下：

     

加法

        必须是同型矩阵才可进行加法，即行、列相同。

      

减法

        必须是同型矩阵才可进行减法，即行、列相同。

       

数乘（区别于乘法，乘法是矩阵乘以矩阵）

      

        以上加法、减法和数乘合称为矩阵的线性代码。

转置

       把矩阵A的行和列互相交换锁产生的矩阵成为A的转置矩阵

      

共轭

        矩阵的共轭定义为:

        

        .一个2×2复数矩阵的共轭如下所示

        

        则

        

共轭转置

        矩阵的共轭转置定义为：

         

        也可以写为：

        

        一个2×2复数矩阵的共轭如下所示：

        

        则

        

乘法

         两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵；

        矩阵的乘法满足以下运算律：

        结合律：

        

        左分配律：

       

        右分配律：

       

        矩阵乘法不满足交换律。

     （注意：当先FEC算法中用到的主要是加法、减法和乘法）

 

Eigen库

简介

       Eigen是一个高层次的C ++库，有效支持线性代数，矩阵和矢量运算，数值分析及其相关的算法。Eigen是一个开源库，从3.1.1版本开始遵从MPL2许可。

       Eigen目前最新的版本是3.3.5，除了C++标准库以外，不需要任何其他的依赖包。Eigen使用的CMake建立配置文件和单元测试，并自动安装。如果使用Eigen库，只需包特定模块的的头文件即可。

       Eigen适用范围广，支持包括固定大小、任意大小的所有矩阵操作，甚至是稀疏矩阵；支持所有标准的数值类型，并且可以扩展为自定义的数值类型；支持多种矩阵分解及其几何特征的求解；它不支持的模块生态系统，提供了许多专门的功能，如非线性优化，矩阵功能，多项式解算器，快速傅立叶变换等。

       Eigen支持多种编译环境，开发人员对库中的实例在多种编译环境下经过测试，以保证其在不同编译环境下的可靠性和实用性。

下载

       下载使用3.3.5，当前的最新版本。

       官网下载地址为：http://eigen.tuxfamily.org/index.php?title=Main_Page#Overview

      

       CSDN的下载地址为：https://download.csdn.net/download/qq21497936/10800291

    

使用Cmake编译成目标dll使用

     （注意：因为编译后的库太大，导致磁盘爆了，笔者没继续编完成）

       当前主要是为了vs2017写c库（c++封装到c库）给c#调用，使用vs2017进行编译。

        CMake是一个工程文件生成工具。用户可以使用预定义好的CMake脚本，根据自己的选择（像是Visual Studio, Code::Blocks, Eclipse）生成不同IDE的工程文件。

        Cmake下载地址：http://download.csdn.net/download/qq21497936/10154545

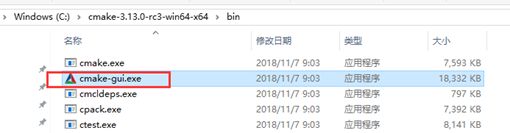
        解压后直接运行cmake-gui.exe

         

        解压Eigen库，并创建目标文件夹eigen-3.3.5_build

       

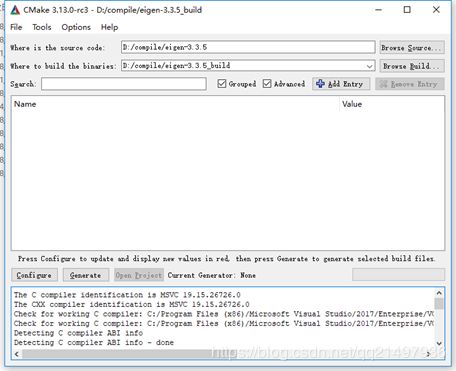
        输入源文件和目标文件夹

        

        点击Configure配置编译器：

        

点击Finish，如下图：

        

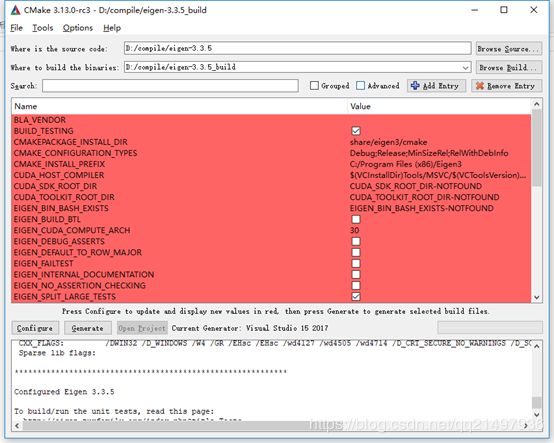
        等待一会儿，Configure完成后会出现一系列配置，如下图（去掉grouped和Advanced的勾选，之前使用过勾选了）：

        

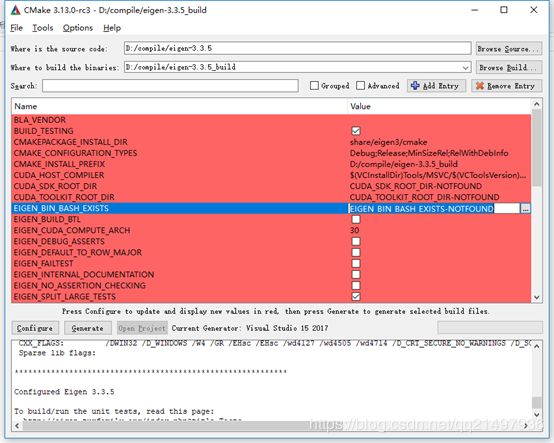
        修改下安装地址，CMAKE_INSTALL_PREFIX

        

       点击Generate，根据配置文件生成相应的工程，完成后如下图：

        

       打开工程，可进入build文件打开工程，也可以使用Open Project按钮打开工程：

        

       编译会需要一段时间，先生成debug，然后清理解决方案，再生成release；

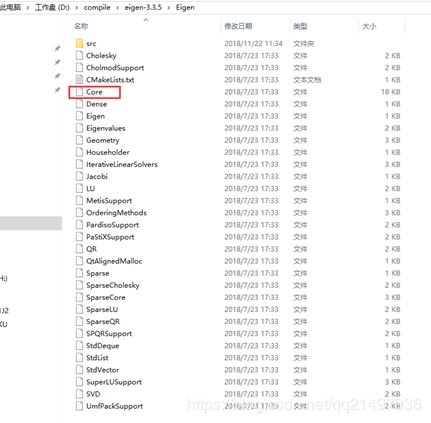
       在编译的过程中，发现出错，调用exe失败，经过检查，是因为把算法库百编译出来的dll实在太大了，检查build文件夹容量（此时该磁盘可用空间已经为0），所以编译这条路貌似不太好走下去，还有一种方式是我们直接包含其源文件到工程中，那么用到那些库生成的文件就会包含哪些，目标文件夹容量如下：

      

       附：若读者第一次使用CMake编译，可能还不理解，可参考下面的篇博文，博文中使用CMake编译Glfw库，可多案例比对分析加深理解：https://blog.csdn.net/qq21497936/article/details/78884842

       

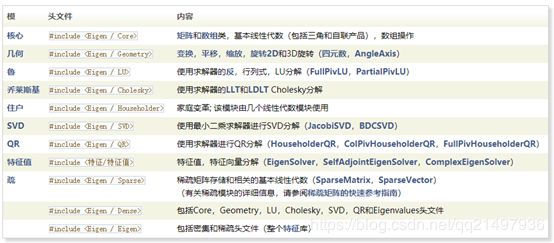
       我们只需要使用到矩阵，所以只需要包含模块头文件和源文件，使用到的库为Core核心库（矩阵和数组类，基本线性代数，数组操作）。

开发配置环境流程以及简单测试

       模块和头文件，每个模块都有一个相应的头文件，必须包含该头文件才能使用该模块。在Dense和Eigen提供的头文件同时方便访问几个模块。

       

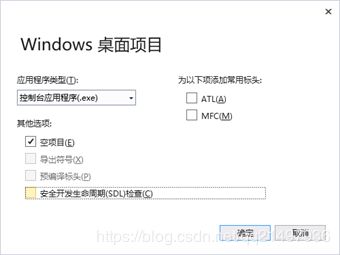
       我们使用VS2017，所以使用VS的VC++建立空工程，如下图：

        

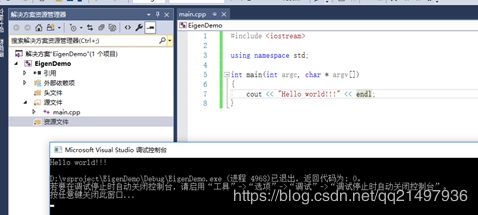
       添加main.cpp文件，建立main函数先跑起来“Hello world！”，如下图：

       

       运行起来后，将Eigen的Core库引入项目，Core模块

       

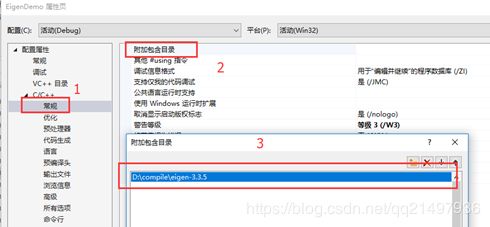
       在VS中添加

       

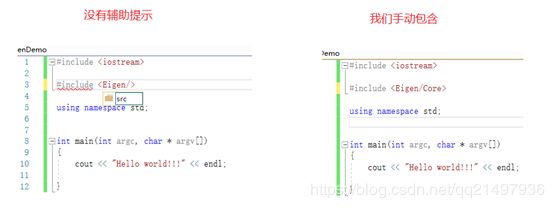
       使用头文件的时候，习惯依赖自动提示，这里特别注意，VS没有提示（如果我们使用自己编译dll包含头文件会有），需要手动添加，提示下图：

       

测试Demo

       测试代码

#include 

#include 

using namespace std;
using namespace Eigen;

int main(int argc, char * argv[])
{
	cout << "Hello world!!!" << endl;
	// 第一种赋值方式，操作有点麻烦，当作数组操作
	MatrixXi A(2, 3);
	A(0, 0) = 1;
	A(0, 1) = 2;
	A(0, 2) = 3;
	A(1, 0) = 2;
	A(1, 1) = 4;
	A(1, 2) = 6;
	// 第二种赋值方式，流式操作，符合C++操作习惯
	MatrixXi B(2, 3);
	B << 0, 1, 0, 1, 0, 1;
	MatrixXi C(3, 2);
	C << 1, 2, 2, 3, 0, 4;
	// 打印A和B
	cout << "A =" << endl << A << endl;
	cout << "B =" << endl << B << endl;
	cout << "C =" << endl << C << endl;
	// 计算A+B
	cout << "A + B =" << endl << A+B << endl;
	// 计算A-B
	cout << "A - B =" << endl << A-B << endl;
	// 计算A*C
	cout << "A * C =" << endl << A*C << endl;
}

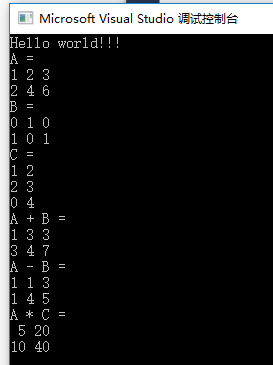
       结果如下：

       

        比对结果：

、

 

原博主博客地址：https://blog.csdn.net/qq21497936
原博主博客导航：https://blog.csdn.net/qq21497936/article/details/102478062
本文章博客地址：https://blog.csdn.net/qq21497936/article/details/84339214