社区发现-Fast Unfolding

一、简介
在社区划分问题中，存在着很多的算法，如由Newman和Gievan提出的GN算法，标签传播算法(Label Propagation Algorithm, LPA)，这些算法都能一定程度的解决社区划分的问题，但是性能则是各不相同。总的来说，在社区划分中，主要分为两大类算法
1.凝聚方法(agglomerative method)：添加边
2.分裂方法(divisive method)：移除边

为了评价社区划分的优劣，Newman等人提出了模块度的概念，用模块度来衡量社区划分的好坏。简单来讲，就是将连接比较稠密的点划分在一个社区中，这样模块度的值会变大，最终，模块度最大的划分是最优的社区划分。
二、模块度的概念
1、模块度的公式
社区划分的目标是使得划分后的社区内部的连接较为紧密，而在社区之间的连接较为稀疏，通过模块度的可以刻画这样的划分的优劣，模块度越大，则社区划分的效果越好 ，模块度的公式如下所示：

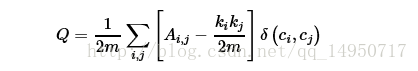
而当u等于v时，函数δ(u,v)的值为1，否则为0
其中Ai,j表示节点i到节点j之间边的权重，Ki表示和节点i相连接的所有边的权重之和

2、模块度公式的简化形式
上述的模块度的计算可以得到以下的简化形式：

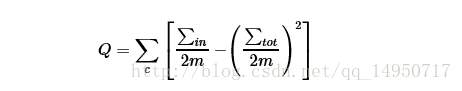
其中，∑in 表示的是社区c 内部的权重，∑tot 表示的是与社区c 内部的点连接的边的权重，包括社区内部的边以及社区外部的边
3、模块度公式的解释
模块度（modularity）指的是网络中连接社区结构内部顶点的边所占的比例，减去在同样的社团结构下任意连接这两个节点的比例的期望值。
三、Fast Unfolding算法
1、Fast Unfolding算法的思路
模块度成为度量社区划分优劣的重要标准，划分后的网络模块度值越大，说明社区划分的效果越好，Fast Unfolding算法便是基于模块度对社区划分的算法，Fast Unfolding算法是一种迭代的算法，主要目标是不断划分社区使得划分后的整个网络的模块度不断增大。
2、Fast Unfolding算法的过程
Fast Unfolding算法主要包括两个阶段
第一阶段称为Modularity Optimization，主要是将每个节点划分到与其邻接的节点所在的社区中，以使得模块度的值不断变大；第二阶段称为Community Aggregation，主要是将第一步划分出来的社区聚合成为一个点，即根据上一步生成的社区结构重新构造网络。重复以上的过程，直到网络中的结构不再改变为止。
具体的算法过程如下所示：
1.初始化，将每个点划分在不同的社区中；
2.对每个节点，将每个点尝试划分到与其邻接的点所在的社区中，计算此时的模块度，判断划分前后的模块度的差值ΔQ是否为正数，若为正数，则接受本次的划分，若不为正数，则放弃本次的划分；
。
3.重复以上的过程，直到不能再增大模块度为止；
4.构造新图，新图中的每个点代表的是步骤3中划出来的每个社区，继续执行步骤2和步骤3，直到社区的结构不再改变为止。
注意：在步骤2中计算节点的顺序对模块度的计算是没有影响的，而是对计算时间有影响

graphx局部实现：
1、vertexstate：

class VertexState  extends Serializable {
  var community = -1L
  var communitySigmaTot = 0L
  var internalWeight = 0L 
  var nodeWeight = 0L;  
  var changed = false
  override def toString(): String = {
    "{community:"+community+",communitySigmaTot:"+communitySigmaTot+
      ",internalWeight:"+internalWeight+",nodeWeight:"+nodeWeight+"}"
  }
}

初始化图

def createLouvainGraph[VD:ClassTag ]( graph:Graph[VD,Long ] ):Graph[VertexState,Long]={
    val nodeWeights = graph.aggregateMessages( nodeWeightMapFunc,nodeWeightReduceFunc,TripletFields.All )
    val louvainGraph = graph.outerJoinVertices( nodeWeights )((id,vd,weightOption) =>{
      val weight = weightOption.getOrElse(0L)
      val state = new VertexState()
      state.community = id
      state.changed = false
      state.communitySigmaTot = weight
      state.internalWeight = 0L
      state.nodeWeight = weight
      state
    }).groupEdges(_+_).partitionBy(PartitionStrategy.EdgePartition2D)
    louvainGraph
  }

Q值的计算：

  def q( currCommunityId:Long,testCommunityId:Long,testSigmaTot:Long,edgeWeightInCommunity:Long,
                nodeWeight:Long,internalWeight:Long,totalEdgeWeight:Long ):Double={
    val isCurrentCommunity = currCommunityId == testCommunityId
    val M = totalEdgeWeight
    val k_i_in_L = if( isCurrentCommunity ) edgeWeightInCommunity + internalWeight else edgeWeightInCommunity
    val k_i_in =  k_i_in_L
    val k_i =  nodeWeight + internalWeight
    val sigma_tot = if (isCurrentCommunity) testSigmaTot - k_i else testSigmaTot
    var deltaQ =  0.0
    if (!(isCurrentCommunity && sigma_tot.equals(0.0))) {
      deltaQ = k_i_in - ( k_i * sigma_tot / M)
    }
     d`
ltaQ
  }

compressGraph

 val internalEdgeWeights = graph.triplets.flatMap(et=>{
      if (et.srcAttr.community == et.dstAttr.community){
        Iterator( ( et.srcAttr.community, 2*et.attr) )
      }
      else Iterator.empty
    }).reduceByKey(_+_)
    val internalWeights = graph.vertices.values.map(vdata=> (vdata.community,vdata.internalWeight)).reduceByKey(_+_)
    val newVerts = internalWeights.leftOuterJoin(internalEdgeWeights).map({case (vid,(weight1,weight2Option)) =>
      val weight2 = weight2Option.getOrElse(0L)
      val state = new VertexState()
      state.community = vid
      state.changed = false
      state.communitySigmaTot = 0L
      state.internalWeight = weight1+weight2
      state.nodeWeight = 0L
      (vid,state)
    }).cache()

    val edges = graph.triplets.flatMap(et=> {
      val src = math.min(et.srcAttr.community,et.dstAttr.community)
      val dst = math.max(et.srcAttr.community,et.dstAttr.community)
      if (src != dst) Iterator(new Edge(src, dst, et.attr))
      else Iterator.empty
    }).cache()

    val compressedGraph = Graph(newVerts,edges)
      .partitionBy(PartitionStrategy.EdgePartition2D).groupEdges(_+_)
    val nodeWeights = compressedGraph.aggregateMessages(nodeWeightMapFunc,nodeWeightReduceFunc)
    val louvainGraph = compressedGraph.outerJoinVertices(nodeWeights)((vid,data,weightOption)=> {
      val weight = weightOption.getOrElse(0L)
      data.communitySigmaTot = weight +data.internalWeight
      data.nodeWeight = weight
      data
    }).cache()

以上是其部分实现的代码；当你计算完毕后，还需要计算connectedComponents组件，用这个去和计算完毕的graph.joinvertices做关联，去规避一些点的社区的划分；该算法的社区划分的效果还是可以得，曾经和某收费的机器学习软件做比较，结果很相近。虽然实现了部分，但是该算法还是有些问题。