OpenGL投影矩阵
目录
1.综述
2.透视投影
3.正交投影
综述
电脑屏幕是2D表面,必须将OpenGL渲染的3D场景作为2D图像投影到计算机屏幕上,所以就需要用到投影变换 M p M_p Mp。首先, M p M_p Mp将所有顶点数据从眼睛坐标转换为裁剪坐标。然后,这些裁剪坐标的各分量(x,y,z)通过除以w分量被变换到规范化坐标(NDC)。所以 M p M_p Mp其实做了两步操作:
- 将相机空间坐标变换到投影空间
- 将投影空间坐标变换到NDC空间
因此,我们必须记住裁剪(视锥体剔除)和NDC变换都集成到了 M p M_p Mp变换中,下面的章节描述了怎样从left、right、bottom、top、near、far这6个参数构造投影矩阵 M p M_p Mp。需要注意的是视锥裁剪是在各个分量( x c x_c xc、 y c y_c yc、 z c z_c zc)除以 w c w_c wc之前完成的。 x c x_c xc、 y c y_c yc、 z c z_c zc通过与 w c w_c wc作比较,如果任何裁剪空间坐标比 − w c -w_c −wc小,或者比 w c w_c wc大这个坐标都将会被丢弃。 − w c < x c , y c , z c < w c -w_c<x_c,y_c,z_c<w_c −wc<xc,yc,zc<wc
然后,OpenGL将重新绘制发生裁剪过的的多边形边缘(如下图所示)。

透视投影
在透视投影中,一个3D点在从金字塔平截头视锥体空间(相机空间)被映射到一个立方体空间(NDC);其各分量范围被如下映射:
x: [l,r]->[-1,1]
y: [b,t]->[-1,1]
z: [-n,-f]->[-1,1]

注意,相机空间是在右手坐标系中定义的,但是NDC使用的是左手坐标系。也就是说,原点处的相机沿着相机空间中 − Z -Z −Z轴看,但是在NDC空间中它是看向 + Z +Z +Z轴的。由于 glFrustum() 的near和far参数只接受正数,所以我们需要在构造投影矩阵的时候需要让他们乘以 − 1 -1 −1变为负数。
在OpenGL中,一个在相机空间的3D点会被投影到近平面(投影平面)上。下图展示了如何将相机空间中的点 ( x e , y e , z e ) (x_e,y_e,z_e) (xe,ye,ze)投影到近平面上 ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp)。
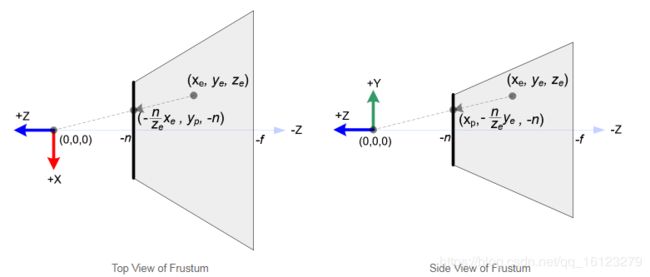
从视锥体的顶视图来看,相机空间的x坐标, x e x_e xe被映射到 x p x_p xp,其通过使用相似三角形的比率来计算,如下所示:

从视锥体的侧视图来看, y p y_p yp也是类似的方式计算:

注意, x p 和 y p x_p和y_p xp和yp取决于 z e z_e ze;他们与 − z e -z_e −ze成反比。换句话说,他们都被 − z e -z_e −ze除。这是构造投影矩阵 M p M_p Mp的第一条线索。在通过乘以 M p M_p Mp矩阵来变换眼睛坐标系之后,裁剪坐标仍然是齐次坐标。它最终需要变为归一化设备坐标(NDC),所以还需要除以裁剪坐标的 w w w分量。

因此,我们可以将裁剪坐标的 w w w分量设置为 − z e -z_e −ze。并且, M p M_p Mp矩阵的第4行变为 ( 0 , 0 , − 1 , 0 ) (0,0,-1,0) (0,0,−1,0)。

接下来,我们将 x p x_p xp和 y p y_p yp映射到具有线性关系的NDC空间的 x n x_n xn和 y n y_n yn:
[l,r]⇒[-1,1]
[b,t]⇒[-1,1]

然后,我们将 x p x_p xp、 y p y_p yp代入上述方程式。

注意,我们使每个方程都除以 − z e -z_e −ze,以进行透视除法 ( x c / w c , y c / w c ) (x_c/w_c,y_c/w_c) (xc/wc,yc/wc).我们之前将 w c w_c wc设置为 − z e -z_e −ze,并且括号内术语变为裁剪坐标系的 x c x_c xc和 y c y_c yc。
从这些方程式中,我们可以找到 M p M_p Mp的第1行和第2行。

现在,我们只有用第3行的 M p M_p Mp来解决。 z n z_n zn与其他算法略有不同,因为相机空间中的 z e z_e ze总是被投影到近平面上的 − n -n −n。但是我们需要用于裁剪和深度测试的唯一 − z -z −z值,并且在以后我们不会去逆变换深度值。由于我们知道z不依赖于x或y值,因此我们借用 w w w分量来找到 z n z_n zn和 z e z_e ze之间的关系,可以像下面这样指定 M p M_p Mp的第3行。
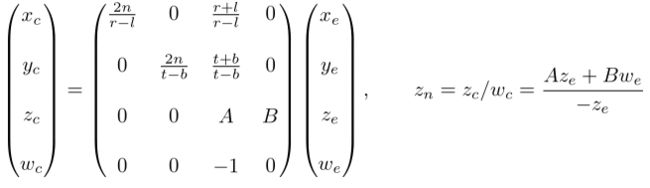
在相机空间中, w e = 1.0 w_e=1.0 we=1.0因此等式变为:
z n = A z e + B − z e z_n= \frac{Az_e+B}{-z_e} zn=−zeAze+B
为了找到系数A和B,我们使用 ( z e , z n ) (z_e,z_n) (ze,zn)的关系; ( − n , − 1 ) (-n,-1) (−n,−1)和 ( − f , 1 ) (-f,1) (−f,1),并将它们放入上面的等式中。

为了求解A和B的等式,重写B的等式(1):
B = A n − n ( 1 ′ ) B=An-n (1') B=An−n(1′)
将方程(1’)代入方程(2)中的B,然后求解A:
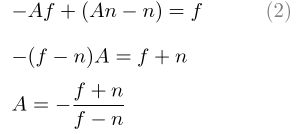
将A放入方程(1)中以找到B :
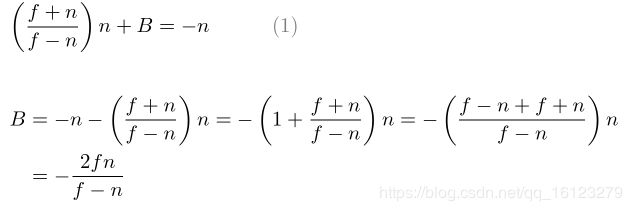
我们找到了A和B,因此 z e z_e ze和 z n z_n zn的变换如下:
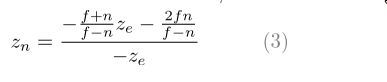
最终,我们找到了全部 M p M_p Mp矩阵的元素,完成的矩阵如下所示:
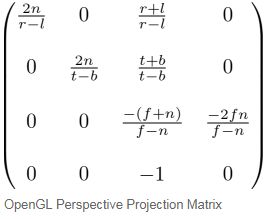
上述矩阵是通用的视锥体矩阵。如果视锥是对称的( r = − l r=-l r=−l和 t = − b t=-b t=−b),那么它可以被简化为如下矩阵:

在离开之前,请再看一下等式(3)中 z e z_e ze和 z n z_n zn的关系。可以注意到它是一个有理函数,并且 z e z_e ze和 z n z_n zn之间是非线性关系。这说明近平面的精度非常高,但远平面的精度非常低。如果范围[-n,-f]越来越大,则会导致深度精度问题(z-fighting);远平面周围的 z e z_e ze的微小变化不会影响 z n z_n zn的值。 n n n和 f f f之间的距离应尽可能短,以最小化深度缓冲精度问题。

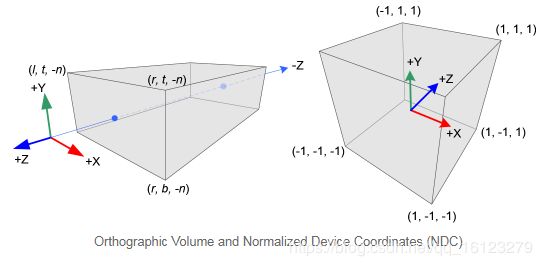
正交投影
构造用于正交投影的 M p M_p Mp矩阵比透视模式简单得多。
眼睛空间中的 所有 x e x_e xe, y e y_e ye和 z e z_e ze分量线性映射到NDC。我们只需要将矩形体积缩放到立方体,然后将其移动到原点。让我们使用线性关系找出 M p M_p Mp的元素。
由于正交投影不需要w分量,因此 M p M_p Mp矩阵的第4行保持为 ( 0 , 0 , 0 , 1 ) (0,0,0,1) (0,0,0,1)。因此,正交投影的完成矩阵如下:

如果视锥体是对称的( r = − l 、 t = − b r=-l、t=-b r=−l、t=−b),进一步简化为: