Tips for Training Deep Neural Network

目录

Activation Function

ReLU激活函数

梯度消失问题

ReLU的缺点及其解决方法

Maxout

Cost Function

Softmax

Cross Entropy

Data Preprocessing

Optimization

Learning Rate

Momentum

Generalization

Early Stopping

Weight Decay

Dropout

---

链接：

http://speech.ee.ntu.edu.tw/~tlkagk/courses/MLDS_2015_2/Lecture/Deep%20More%20(v2).pdf

这节是关于DNN的一些优化技巧，都是硬功夫。以前我觉得自己对这些东西理解得挺不错的，但是学习了之后感觉原来都是皮毛。这一部分我也是通过自己已有的知识量去整理的笔记，可能表述有些地方不对的，还请读者纠正和指出，谢谢。

Activation Function

ReLU激活函数

ReLU激活函数是2011年提出来的，那一年Hitton和Andrew都提出了类似的方法。但是在此之前，人们都一直只用Sigmoid函数，为啥使用呢？Hitton在一次演讲中也回答了这个问题，他说：“我自己感觉活得时间过长，那时候正好赶上选用什么激活函数在神经网络中，最终选择了sigmoid，其实也没啥原因。”哈哈哈，好吧，感觉很扯，但这句话确实是他说的。

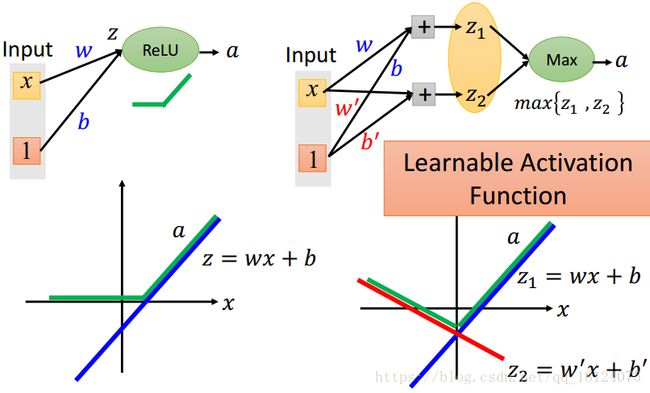
现在激活函数通常是选择ReLU， 它在z>0时，微分为1；z<0时，微分为0；z=0时，取0或1都行。ReLU被选择的原因有四个：

1. Fast to compute

2. Biological reason (Andrew) 跟人脑的神经脉冲很像，当z<0时，神经元是没有信号的。但是在sigmoid中，当z=0时，神经元输出为0.5，就是说神经元无论何时将会处于亢奋的状态，这与实际情况是相违背的。

3. Infinite sigmoid with different biases (Hitton) ReLU的形状和多个sigmoid函数累加和的形状很像。所以，我们可以理解为ReLU是sigmoid的一个进化版。

4. Vanishing gradient problem 这一点才是最重要的，下面我们将会进一步解释。

梯度消失问题

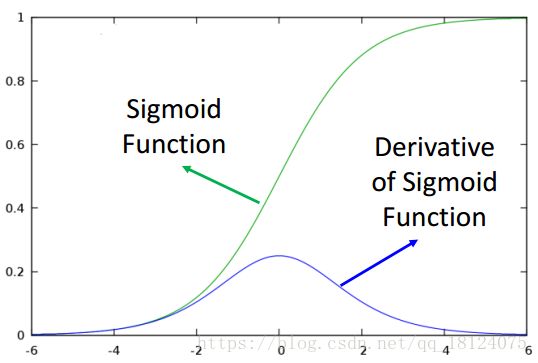
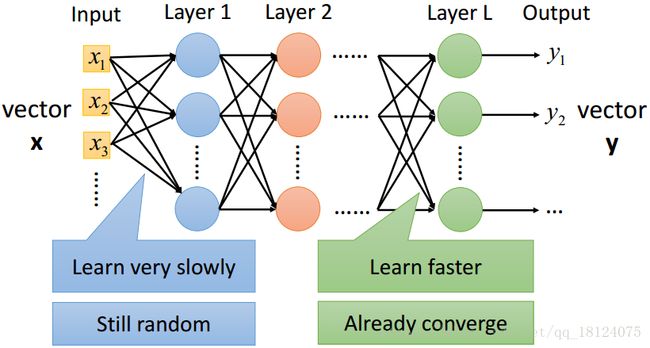
由第一张图，我们可以知道sigmoid的微分是一个小于0的数。所以我们再看图二，随着每一层的残差反向递推的计算，每次乘以一个小于0的数，层数增加了，乘以小于0的数的次数也会增加。Oops~最终残差会趋向0，这可不是我们想看到的结果。

除此之外，还会出现一个很尬的情况，因为现在layer 2 层的残差为一个特别小的数，所以权值和偏置不会更新，其结果会和刚开始初始化设置得参数值差不多。在layer L层的时候，这里的权值和偏置更新特别快，估计早就饱和收敛了吧。

以上是反向传播，对于前向传播来说，Layer 1层得到一个input，每次乘以一个小于0的数（sigmoid的范围为0~1），到最后Layer L层的输入几乎趋近0，所以不会对最后层有任何影响。

补充：对于梯度爆炸问题，当激活函数的微分永远大于1，每一层的参数都会变得越来越大，无论是前向传播还是后向传播，分析方法和上面一样。

ReLU的缺点及其解决方法

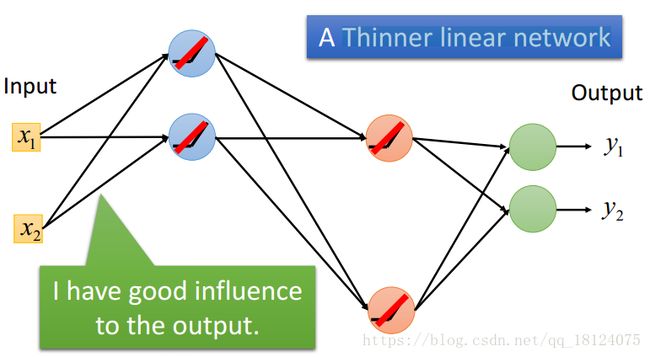
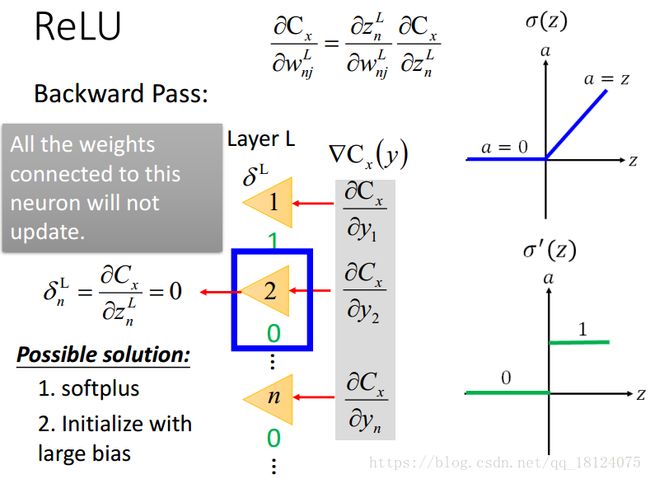
因为ReLU激活函数有一部分全为0，就可能出现一部分神经元的输出是0，从而导致在反向传播求残差的时候不能得到权值的更新。不过呢，其实没啥大问题，我们因此也会得到一个更瘦且长的神经网络，而且对输出的影响也可能会更好。但是，这里会有一个可怕的问题，万一某一层的神经元都是0，那么这个网络就废了。

解决办法：softplus f(x)=ln(1+exp(x)), 避免为0; 初始化的时候设一个很大的偏置，这样会让输入激活函数的z变大，从而让非零的地方更少。但是，实际上大部分都不会更新，所以这两种解决方法并没有多大的提升。

现在比较好的是对ReLU进行变形，改成Leaky ReLU。

Maxout

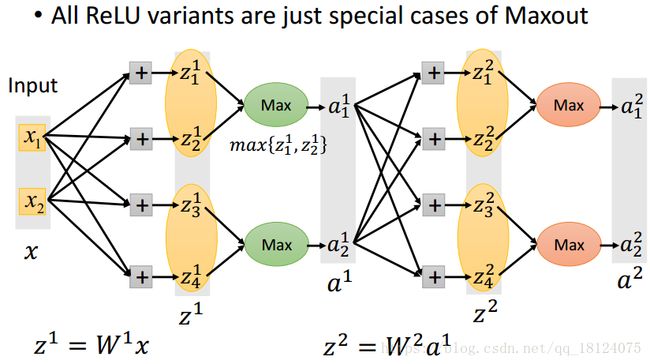
前面我们说到的ReLU是Maxout的一个特例。Maxout才是常态，它被提出来是在2013年之后。这里，每一层的max{zi,zj,zk}，这些zi, zj, zk都是在训练之前被分好了的，max{}里面的也可以不止3个，z1和a1的数目是不相等。

这个Maxout神奇之处在于能够根据data自动地被学习出来，所以没有固定的函数。Z越多，学习越复杂，input和output的关系越复杂，这是ReLU做不到的。

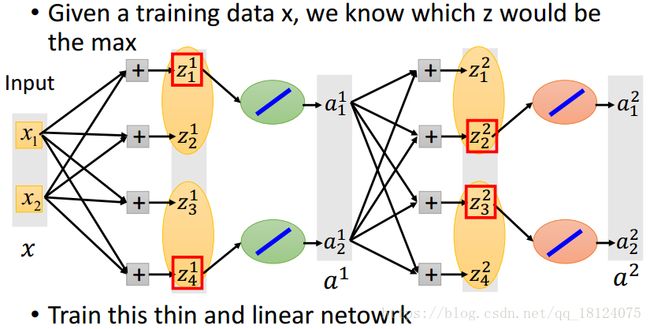
在每一层的max{zi,zj,zk}中，选取比较大的z北直街复制到a中，同时比较小的z当作不存在，直接被拿掉。所以说，在反向传播的时候，我们将其当作一个线性的网络训练即可。

这里有人可能会想：那些比较小的z被拿掉，不就是相当于坏死了吗？不会的，因为当比较小的那个节点在下一次前向传播的时候再次参与计算，说不定就会变成比较大的数，从而被选中并且再次连接。

Cost Function

损失函数的思考，我在BP反向传播的时候就在思考。损失函数就是一个定义预测值与真实结果好坏的东西。图中两个预测值，如果我们用距离与真实值去比较，肯定第一个结果要好；如果我们用出现概率可能性来比较，肯定第二个不错。所以说，我们是不是需要用什么东西统一一下呢？

Softmax

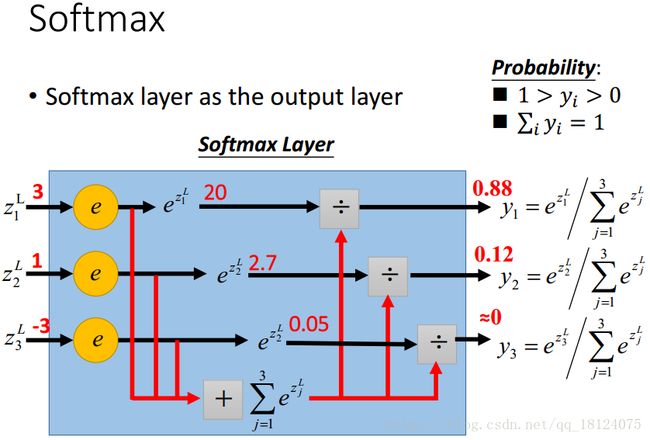
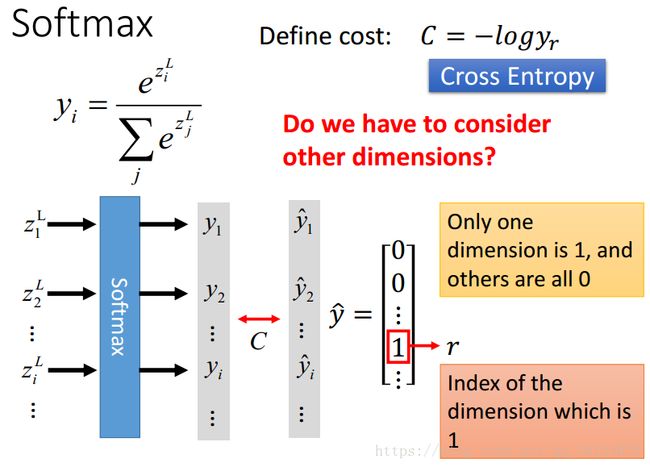
擒贼先擒王，我们先别管损失函数。先在输出层下功夫，使用softmax激活函数对输出结果进行归一化，这样就可以做比较了。

选择了softmax激活函数之后，新的问题也来了，我们选择softmax对应的什么损失函数呢？选择损失函数的标准一般是要产生比较大误差，才能产生比较大的残差，从而才能更好地找到对应的gradient。这里，我们并不希望错的就好，这里差生一个比较大的误差，是对错误很敏感，有一点错误就可以得到放大。

 

Cross Entropy

这里，我们选择了交叉熵，且只需要考虑结果为r(1)的部分。因为yr + rother = 1，所以一个没问题，另外一个也是固定的。

由图中残差与输出结果可以知道，它们是成正比关系。这张图是对于y=1的部分，y=0的部分，残差和输出结果的关系也是成正比的。

 

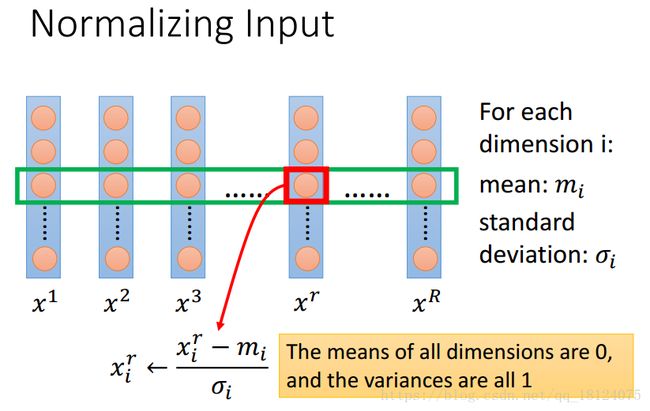
Data Preprocessing

数据预处理部分没啥好说，就是需要对数据进行归一化，能更好的地迭代和梯度下降。

Optimization

在深度学习需要优化的两个问题中，我们主要解决两个事儿。1. How to determine the learning rates；2. Stuck at local minima or saddle points.

Learning Rate

对于学习率的选取，不同参数的初始化会有不同的影响，具体学习率的选择范围是根据data调整决定。

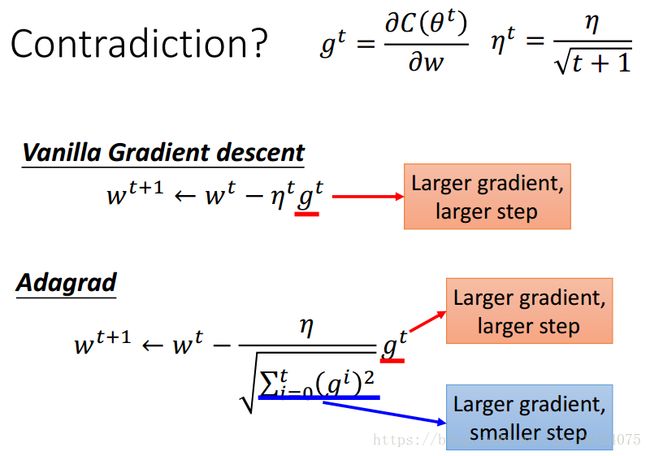
通常情况下，我们在初始的时候，学习率一般设置比较大；在经过一定次数的迭代后，我们可以让学习率衰减一点儿。但是这个度去怎么控制，一直都是一个问题，解决的方法有很多，其最高境界是需要去调学习率，让神经网络自动地去调节。这里，我们采用Adagrad方法：

 

在Adagrad中，除了学习率本身会随着时间衰减之外，还会除以过去所以gradient平方和的平均数再开根号。最后整理一下，学习率/过去所以gradient平方和再开根号。

在简单梯度下降法中，学习率越大的话，step会跟着变大，也就是说step变大的原因是由学习率增大造成的。

在Adagrad中，gradient越大，step本来就应该很大；但是在分母中，gradient越大，学习率会变小，导致step也会变小。感觉相互矛盾，其实不然，这是一种反差效果。

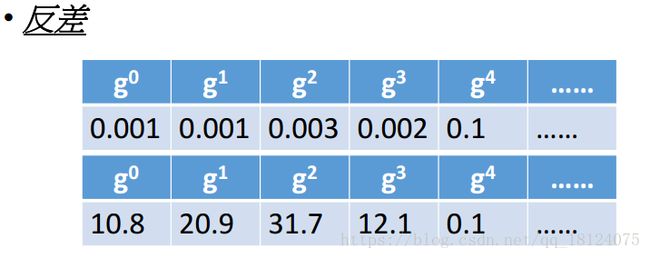
当前面的g太小，会导致后面的g变大；当前面的g太大，会导致后面的g变小。

对于不同的参数，在自己的梯度下降中，离局部最优点越远，且越陡的地方下降速度越快。但是不同参数之间怎么去比较呢？最好的方法是上图红框中的，用一阶微分的绝对值除以二阶微分，但是这样做的代价就是会增加计算量。比如：二阶微分计算的时间远远大于在一阶梯度下降法中收敛的时间，要是这样的话，将会是没有任何意义的。

所以基于此，Adagrad就是通过一阶微分去估算二阶微分，从而达到最好的best step的效果。这里，二阶微分一般是一个常数。

 

Momentum

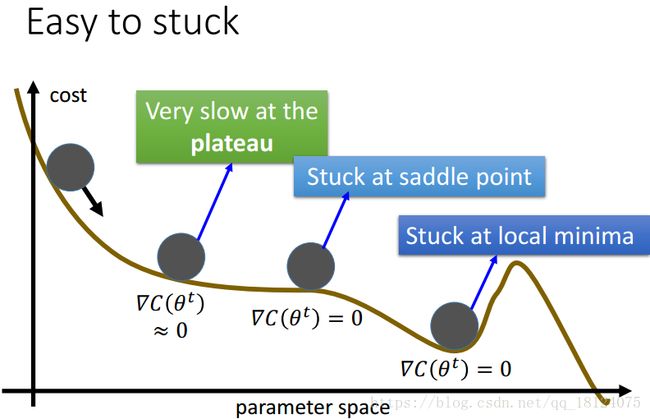
梯度下降和正常的物理下降不一样，在plateau的时候，代价函数的微分约等于0，下降速度回减慢，甚至可能停下来；在saddle point的时候，代价函数的微分为0，但是此时并并不是极值的点；在loacal minima的时候，代价函数的微分为0，但是此时后面还有更小的loss。

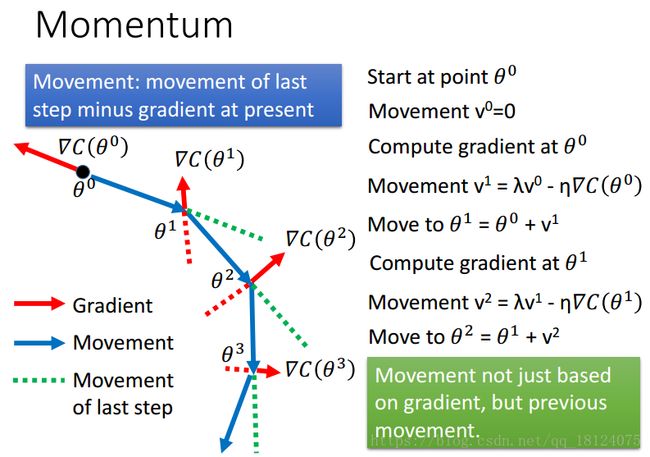
为了模仿这种物理的惯性效果，我们引入冲量的概念，在这一个时刻加上上一个时间点的方向，从而决定下一次的方向。刚开始的时候，冲量v设为0，第一次迭代和正常的一样，在第二次中，更新方向是由梯度下降与上一次的梯度下降共同决定的。其实，在t时刻的冲量等于从1~t-1时刻的所有梯度之和，1时刻的系数会乘上一个更小的数，从而使得越早的梯度对当前下降方向的影响是最小的。

 

Generalization

对于泛化能力比较差的时候，最简单的方法有两种，Have more training data；Create more training data。其中，创建更多的数据可以将原始数据进行变形，比如图像放大、缩小、对称、上下移动等。语音加速、慢速等。

Early Stopping

为了防止过拟合，需要过早结束，而且需要使用验证集，而并不是测试集。目前来说Early Stopping还没有明确的方法。

 

Weight Decay

需要加一个惩罚项去平衡权值，这是因为w在t时刻会乘以一个小于1的数，所以需要加一个惩罚项去防止w一直变小。这也是防止过拟合的一种方法。对于惩罚项一般有一范(Lasso)，二范(Ridge Regression), 一范+二范(Elastic Net)。除此之外也可以自己的设计，类似的文献有很多。

 

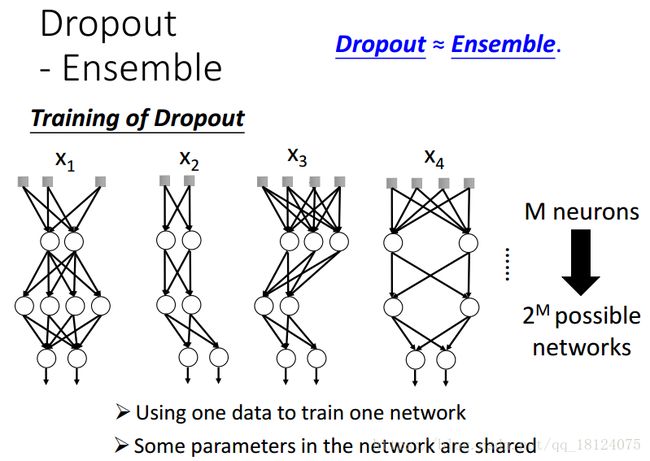
Dropout

对于在训练集中的dropout，每次迭代需要重采样需要被dropout的神经元。在每次迭代中，部分神经元被dropout，就会形成一个新的网络，我们需要使用这个新的网络去训练。这里，我们需要注意一下：比如我们每层需要1000个神经元，但是dropout是0.5，所以在实际中我们需要设置2000个神经元。

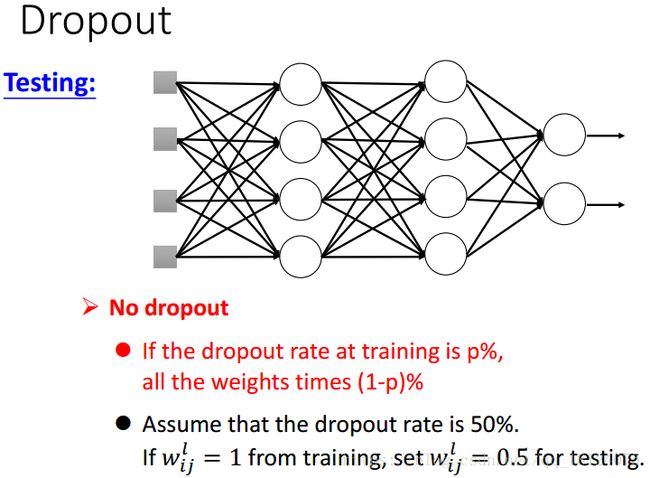
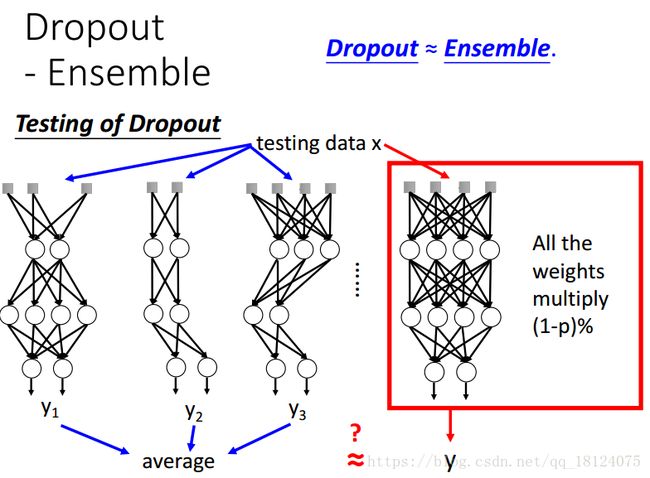
对于在测试集中的dropout，我们不需要进行dropout，但是对于权值来说，我们需要乘以dropout的值进行放缩。比如，在训练集中某个神经元的权值为1，那么在dropout=0.5的情况下，测试集中该神经元的权值就为0.5。

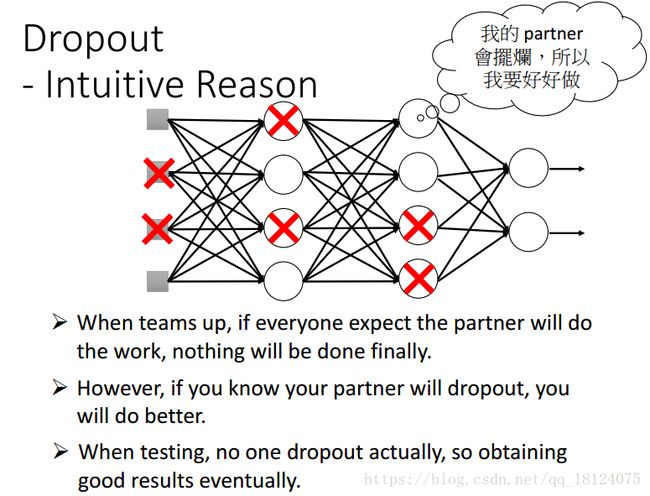
为啥dropout网络效果比非dropout效果好？

举个栗子，在组队做项目中，每个人都希望自己的队友能够做项目，并把它做得很好，这样就不需要去做了，类似于三个和尚没水喝的道理，结果大家都这么想，然后大家都没做，效果特别差。如果，我们把队友提出，就让一个人去做，没有了任何依靠，所以这个人就不得不做，类似于一个和尚有水喝的道理，结果做得还可以。但是在测试中，没有任何人被dropout，大家也都想努力把这个事儿做好，于是结果就会特别理想。

Dropout的宗旨就是Ensemble。在训练中，每次都对数据进行采样，每次dropout都是随机的，所以会得到不同的神经网络，我们对得到的结果取平均。

在测试中，如果用训练的方法会费时费力，幸好我们可以把训练中的不同网络每一层的权值全部相乘得到测试集中的每一层网络，一样可以得到相同的效果。但是这种等价不是绝对的，不是所以的条件下都成立。这里，训练相乘为什么可以表示成测试网络的权值依然是一个未解之谜。

 

在dropout的时候，我们需要注意实际的神经元数量肯定是比需要的神经元数量多；加入dropout训练时间会加长，所以在初始化的学习率也需要更高，需要更大的冲量。