分治法（递归）代码的理解与编写

分治法，即分而治之，将一个复杂问题划分成若干个相同性质的子问题进行求解，最后再”合治“为初始问题的解。在数据结构课程中求解”最大子列和“的问题中就有用到这一经典算法，而分治法往往需要通过递归进行实现。

接下来，我们就以”最大子列和“问题为切入点，通过一步步书写代码，进一步理解这一算法思想及实现过程。

【问题描述】给定n个整数的序列{a1，a2，…，an}，求函数f(i,j)=max{0，${\sum }_{k=i}^j{a}_k$}的最大值。
在这里，”子列“被定义为原始序列中连续的一段数字，我们要找出的是具有最大和的一段连续的子列，并且返回它的和。如果这个最大和是负数，那么我们取0为最终答案。

【算法实现】分治，即把大问题分成小问题进行解决，那么求一整数序列的最大子列和是不是可以看成把该整数序列分成左右两半，分别求得左半部分和右半部分的最大子列和，以及跨越左右边界的最大子列和，这三个最大子列和中最大的那个呢？
那么，我们的程序可以写为：

/*与主函数的接口 长度为N的整数序列*/
int MaxSubseqSum(int List[], int N)
{
	return DivideAndConquer(List,0,N-1);
}

/*分治法求最大子列和*/
int DivideAndConquer(int List[], int left, int right)
{
	/*分*/
	int center, i;
	center = (left + right) / 2; /*找到中分点*/
	int MaxLeftSum, MaxRightSum; /*左半部分与右半部分的最大子列和*/
	int MaxLeftBorderSum, MaxRightBorderSum; /*从边界向两侧扫描的跨越边界的最大子列和*/
	/*治*/
	return Max(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum); /*问题的结果：三个最大子列和中最大的那个*/
}

/*返回三个数中最大的那个数*/
int Max(int A, int B, int C)
{
	return A > B ? A > C ? A : C : B > C ? B : C;
}

那么，确定了程序的主体框架后，怎么进一步求解这三个最大子列和呢？
对于这个问题，我们可以采用递归的思想进行解决，即把锅甩给左右两个整数序列，让它们进行求解，得到结果后再返回来，并与跨越边界的结果进行比较，返回这三个子列和中最大的数作为最终结果。

那怎么通过程序语言实现甩锅呢？

我们知道这里的甩锅其实就是递归，把问题交给子问题进行求解，得到结果后再返回来，具体怎么实现交给计算机去解决，我们等着收割就好了。其中计算机能否一步一步向前迭代，最后再返回我们想要的值，还需要我们正确设置好两个约束。

a)递推关系 和 b)终止条件。

对于本问题，我们可以进行如下分析：

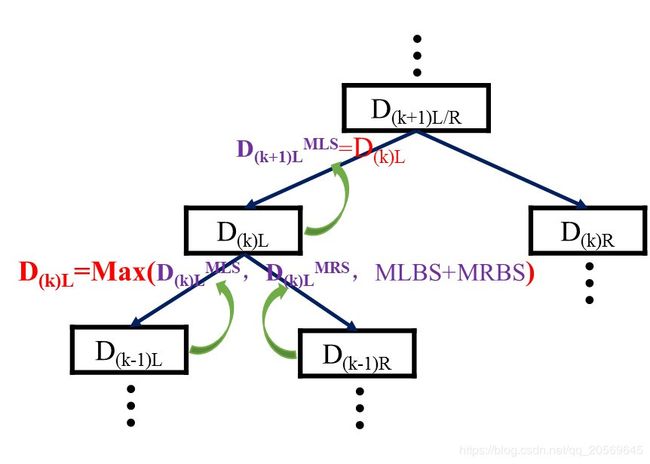
其中D表示DivideAndConquer函数，下标k表示第k次迭代，k+1、k-1同理，下标L、R表示左、右半部分整数序列，上标MLS、MRS分别表示MaxLeftSum和MaxRightSum，MLBS+MRBS表示MaxLeftBorderSum + MaxRightBorderSum，绿色箭头表示返回。

如上图所示，取第k次迭代进行分析，$D_{kL}$可以分成两半部分，即左半部分$D_{(k-1)L}$和右半部分$D_{(k-1)R}$，而$D_{kL}$函数运行完的返回值，即为该部分整数序列的最大子列和（因为如果$D_{kL}$是最终迭代的话，其返回的应该是问题的解，最大子列和），即

$D_{kL}$=Max($D_{kL}^{MLS}$，$D_{kL}^{MRS}$，MLBS+MRBS)；

而$D_{kL}^{MLS}$和$D_{kL}^{MRS}$，我们可以将其扔给第k-1次迭代进行求解，即

$D_{(k-1)L}$=$D_{kL}^{MLS}$，$D_{(k-1)R}$=$D_{kL}^{MRS}$；

这样层层递归，把k-1层的结果返回给k次，作为k层的MaxLeftSum和MaxRightSum，而k层知道MaxLeftSum和MaxRightSum后，再计算MaxLeftBorderSum + MaxRightBorderSum的值，比较这三个结果的大小，把最大的那个数返回给k+1层，作为k+1层的MaxLeftSum，这样就完成了递归链。

其中递归的终止条件为，左右两半部分均不可继续划分、调用。

上面这一过程用程序语言描述即为：

/*终止条件：子列只有一个数字*/
if (left==right)
{
	if (List[left] > 0)
		return List[left];
	else
		return 0;
}

/*甩锅过程*/
MaxLeftSum = DivideAndConquer(List, left, center); /*下一次调用的结果作为（返回为）本次的MLS*/
MaxRightSum= DivideAndConquer(List, center+1, right); /*下一次调用的结果作为（返回为）本次的MRS*/
return Max(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum);  /*本次的MLS、MRS、MLBS+MRBS中最大的值作为（返回为）上一次的ML/RS*/

其中每一次甩锅过程都要计算MLBS+MRBS，对于跨越边界的最大子列和可以通过for循环来实现，分别从中间向两侧扫描相加，记录最大的结果作为MaxLeftBorderSum和MaxRightBorderSum，即：

/*求解跨越边界的最大子列和*/
int LeftBorderSum, RightBorderSum;

/*左半边，从中间向左边扫*/
MaxLeftBorderSum = 0; LeftBorderSum = 0;
for (i = center; i >= left; i--)
{
	LeftBorderSum += List[i];
	if (LeftBorderSum > MaxLeftBorderSum)
		MaxLeftBorderSum = LeftBorderSum;
}

/*右半边，从中间向右边扫*/
MaxRightBorderSum = 0; RightBorderSum = 0;
for (i = center + 1; i <= rightt; i++)
{
	RightBorderSum += List[i];
	if (RightBorderSum > MaxRightBorderSum)
		MaxRightBorderSum = RightBorderSum;
}

将上面的代码合在一起，即为最大子列和分治法的最终完整代码。

/*返回三个数中最大的那个数*/
int Max(int A, int B, int C)
{
	return A > B ? A > C ? A : C : B > C ? B : C;
}

/*分治法求最大子列和*/
int DivideAndConquer(int List[], int left, int right)
{
	/*分*/
	int center, i;
	int MaxLeftSum, MaxRightSum; /*左半部分与右半部分的最大子列和*/
	int MaxLeftBorderSum, MaxRightBorderSum; /*从边界向两侧扫描的跨越边界的最大子列和*/

	/*终止条件：子列只有一个数字*/
	if (left == right)
	{
		if (List[left] > 0)
			return List[left];
		else
			return 0;
	}

	center = (left + right) / 2; /*找到中分点*/
	/*甩锅过程*/
	MaxLeftSum = DivideAndConquer(List, left, center);
	MaxRightSum = DivideAndConquer(List, center + 1, right);

	int LeftBorderSum, RightBorderSum;
	/*求解跨越边界的最大子列和*/
	/*左半边，从中间向左边扫*/
	MaxLeftBorderSum = 0; LeftBorderSum = 0;
	for (i = center; i >= left; i--)
	{
		LeftBorderSum += List[i];
		if (LeftBorderSum > MaxLeftBorderSum)
			MaxLeftBorderSum = LeftBorderSum;
	}

	/*右半边，从中间向右边扫*/
	MaxRightBorderSum = 0; RightBorderSum = 0;
	for (i = center + 1; i <= rightt; i++)
	{
		RightBorderSum += List[i];
		if (RightBorderSum > MaxRightBorderSum)
			MaxRightBorderSum = RightBorderSum;
	}


	/*治*/
	return Max(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum); /*问题的结果：三个最大子列和中最大的那个*/
}

/*与主函数的接口 长度为N的整数序列*/
int MaxSubseqSum(int List[], int N)
{
	return DivideAndConquer(List, 0, N - 1);
}

希望本文能够让大家对递归调用实现分治算法有更进一步的认识。

同时也欢迎大家关注我的公众号，赵小赵的编程哲学（微信号：zxzdbczx），不定期更新C语言学习过程中的一些心得感悟。