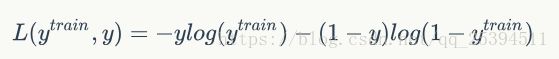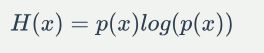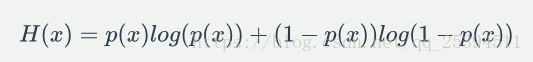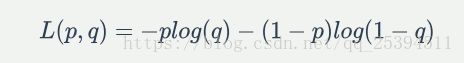神经网络基础-logistic回归

logistic回归

数学推导

logistic回归是机器学习中一个基础的用于分类的方法，在此讨论二类分类，训练集由带有标签1或0的样本集合X组成，我们需要学习的是一种映射关系

该映射关系的参数为,在logistic学习中,实际过程是学习合适的参数使得预测值与的差越小。 
上述过程即为最大似然估计法，也是logistic回归的损失函数的推导依据。下面详细说明整个过程。 
logistic回归本质是一种线性回归，只是在分类的时候加入了非线性变换函数sigmoid()来使得可以和标签进行直接比较，这个非线性变换在深度学习中被称为激活函数，有多种选择方法。预测过程可以分为两步，均以矩阵来计算：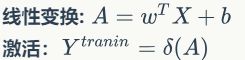 
 
得到的即为学习的预测值，需要比较它和实际值的误差，因此会引入代价函数（损失函数），只有通过代价函数，我们才能评估参数值的选取是否合适，然后前馈修改参数。在logistic回归中，我们用到的损失函数是交叉熵函数:

首先我们弄清楚为什么会选取这个函数，信息论中信息熵的定义一般是

如果X的取值只有两种，那么就是

引入相对熵（KL散度）的概念，如果对于一个变量或者样本集，用P分布或者Q分布均可以，KL散度是两个概率分布P和Q差别的非对称性的度量,所以相对熵有非对称性。典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。

D越小代表两个分布的差别越小，对D展开：

p代表真实分布，因此是个定值，所以后一部分即可度量p,q的分布距离，-plogq定义为交叉熵，若p,q为二项分布，则可以定义交叉熵为:

我们的目的是得到最小的损失函数,在计算过程中，我们会计算每一个样本的损失函数，然后累加，得到整个样本的损失函数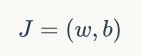

该式子表示选择参数为w,b的总损失函数.

对于每一个样本计算一次样本损失，每一个该过程都可以看作一个神经元运算，因此logistic可以算是一个最简单的神经网络。 
到此正向传播过程已经结束，然后是反向传播，即为了需要得到最小的J(w,b),需要反馈回第一步w,b的选取，该过程采用梯度下降法,a代表步进长度=学习率。 

python实现

下面我们就可以愉快使用上面几个公式在python中完成酷炫的logistic学习。 
实现的过程参照的是大帅吴的deep learing课，训练集为209个64*64像素的猫片,标签为是猫和不是猫（1，0），测试集为50个样本。

第一步：导入数据集

该部分实现了h5数据集的导入，需要

得到的数据为训练的输入输出，测试的输入输出，分类区间。前四个数据还需要进一步处理。

第二步：数据处理

数据集是209个图片，每个图片是64*64个像素点，每个像素点是RGB，该步骤就是将像素数据排成一维，方便计算。

第三步：建立模型

这一步的主要作用是导入数据，初始化参数，然后调用优化过程训练参数，最后进行测试。

第四步：建立优化函数

在这一步需要建立上一步中调用的optimize函数

该函数传入，初始化为0的w,b，维度化和归一化后的训练集，训练集标签，迭代次数，学习率。下面分析一次迭代： 
一次迭代过程第一步就是计算正向和反向过程：

计算出dw,db后就进行梯度下降，返回更新后的w,b。

第四步：建立预测函数

传入预测集（训练集或者测试集均可），计算 

然后与0.5比较，大于1则为1，反之为0.

总结

通过以上步骤，我们就可以实现logistic回归的学习以及测试。最后也可以尝试观测一下不同的学习率或者迭代次数对于学习效果的影响。 
logistic回归其实还有很多的内容，例如梯度下降算法其实不是唯一选择，还有牛顿法，拟牛顿法，后两者的收敛速度其实会更快一点。还有损失函数的选择，为什么不用最常用的MSE：均方误差。有两种思路，一种是通过本文开始提到的最大似然估计，可以推导出对数损失函数满足经验风险最小化。另外一种思路是吴恩达讲的，均方误差函数累加后是非凸函数，有多个局部最小值，如果步进或者迭代设置稍微出错，就很容易收敛不到全局最优值。

代码可以在http://github.com/qusongyun/logistic  

博文原版：https://qusongyun.github.io