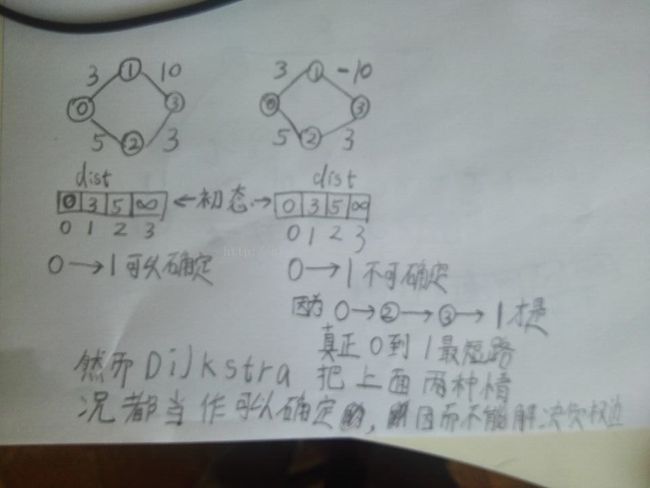
单源有权图的最短路径 Dijkstra算法(证明不能解决负权边)7.1.2
单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路径。
Dijkstra算法
假设存在G=
U中收录的是已确定的最短路径顶点,比如2被U收录的话就代表dist[2]的值就是顶点0到顶点2的最短路径,后面操作不需要再更新它。
步骤如下
初始化:dist[i]=0->i,U={0},path[0]=-1。(->这里表示图中顶点到另一顶点的权重)
循环:
1、路径中不包括负权边的情况下未收录顶点中dist值最小的就是真正的最短距离,收录到U中,用于标记它已经确定了,后面不需要再更新它。
2、上一步确定一个顶点V后,此顶点V的邻接点W的dist值可能受到影响(除去U收录的顶点外:dist[W]=MIN(dist[W],dist[V]+V->W),path[W]=V;)。
3、重复以上步骤直到U收录了所有顶点,i属于任何顶点时此时dist[i]都表示真正的(已确定)最短距离
证明不能解决负权边
C语言代码实现如下
#include
#include
#include
#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/
#define MaxVertexNum 100 /* 最大顶点数设为100 */
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
bool U[MaxVertexNum];
int dist[MaxVertexNum];
int path[MaxVertexNum];
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边 */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
WeightType Weight; /* 边权重 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge;/* 边表头指针 */
DataType Data; /* 存顶点的数据 */
/* 注意:很多情况下,顶点无数据,此时Data可以不用出现 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
LGraph CreateGraph( int VertexNum )
{ Vertex V;
/* 初始化一个有VertexNum个顶点但没有边的图 */
LGraph Graph=(LGraph)malloc(sizeof(struct GNode));
Graph->Nv=VertexNum;
Graph->Ne=0;
/* 初始化邻接表头指针 */
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V=0; VNv; V++)
Graph->G[V].FirstEdge = NULL;
return Graph;
}
void InsertEdge( LGraph Graph, Edge E ) {
PtrToAdjVNode NewNode;
/* 插入边 */
/* 为V2建立新的邻接点 */
NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V2;
NewNode->Weight = E->Weight;
/* 将V2插入V1的表头 */
NewNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = NewNode;
/* 若是无向图,还要插入边 */
/* 为V1建立新的邻接点 */
NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V1;
NewNode->Weight = E->Weight;
/* 将V1插入V2的表头 */
NewNode->Next = Graph->G[E->V2].FirstEdge;
Graph->G[E->V2].FirstEdge = NewNode;
}
LGraph BuildGraph()
{
LGraph Graph;
Edge E;
Vertex V;
int Nv, i;
scanf("%d", &Nv); /* 读入顶点个数 */
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */
scanf("%d", &(Graph->Ne)); /* 读入边数 */
if ( Graph->Ne != 0 ) { /* 如果有边 */
E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */
/* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */
for (i=0; iNe; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
/* 注意:如果权重不是整型,Weight的读入格式要改 */
InsertEdge( Graph, E );
}
free(E);
}
/* 如果顶点有数据的话,读入数据 */
for (V=0; VNv; V++)
scanf(" %c", &(Graph->G[V].Data));
return Graph;
}
void Dijkstra(LGraph Graph,Vertex V){
//初始化
for(int i=0;iNv;i++)
{dist[i]=INFINITY;U[i]=false;}
PtrToAdjVNode W=Graph->G[V].FirstEdge;
for(;W;W=W->Next)
dist[W->AdjV]=W->Weight;
dist[V]=0;U[V]=true;
///////////////
while(true){
//
int Min=INFINITY;
Vertex j;
for(int i=0;iNv;i++)
if(Min>dist[i]&&U[i]==false)
{Min=dist[i];j=i;}
printf("%d\n",Min );
if(Min==INFINITY)
break;
U[j]=true;//找到最小的dist收录
printf("%d->%d %d->%d[%d]\n",path[j],j,V,j,dist[j]);
//
W=Graph->G[j].FirstEdge;
for(;W;W=W->Next)//对邻接点dist进行更新操作
if(dist[W->AdjV]>dist[j]+W->Weight&&U[W->AdjV]==false)
{dist[W->AdjV]=dist[j]+W->Weight;path[W->AdjV]=j;}
}
}
int main(){
LGraph Graph=BuildGraph();
Dijkstra(Graph,0);
return 0;
} #include
#include
#include
#define MaxVertexNum 100 /* 最大顶点数设为100 */
#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
bool U[MaxVertexNum];
int dist[MaxVertexNum];
int path[MaxVertexNum];
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边 */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
DataType Data[MaxVertexNum]; /* 存顶点的数据 */
/* 注意:很多情况下,顶点无数据,此时Data[]可以不用出现 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
MGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
Vertex V, W;
MGraph Graph;
Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */
Graph->Nv = VertexNum;
Graph->Ne = 0;
/* 初始化邻接矩阵 */
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V=0; VNv; V++)
for (W=0; WNv; W++)
if(V==W)
Graph->G[V][W]=0;
else
Graph->G[V][W] = INFINITY;
return Graph;
}
void InsertEdge( MGraph Graph, Edge E ) {
/* 插入边 */
Graph->G[E->V1][E->V2] = E->Weight;
/* 若是无向图,还要插入边 */
Graph->G[E->V2][E->V1] = E->Weight;
}
MGraph BuildGraph()
{
MGraph Graph;
Edge E;
Vertex V;
int Nv, i;
scanf("%d", &Nv); /* 读入顶点个数 */
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */
scanf("%d", &(Graph->Ne)); /* 读入边数 */
if ( Graph->Ne != 0 ) { /* 如果有边 */
E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */
/* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */
for (i=0; iNe; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
/* 注意:如果权重不是整型,Weight的读入格式要改 */
InsertEdge( Graph, E );
}
free(E);
}
/* 如果顶点有数据的话,读入数据 */
for (V=0; VNv; V++)
scanf(" %c", &(Graph->Data[V]));
return Graph;
}
void Dijkstra(MGraph Graph,Vertex V){
//初始化
for(int i=0;iNv;i++)
{dist[i]=Graph->G[V][i];U[i]=false;}
dist[V]=0;U[V]=true;
///////////////
while(true){
//
int Min=INFINITY;
Vertex j;
for(int i=0;iNv;i++)
if(Min>dist[i]&&U[i]==false)
{Min=dist[i];j=i;}
if(Min==INFINITY)
break;
U[j]=true;//找到最小的dist收录
printf("%d->%d %d->%d[%d]\n",path[j],j,V,j,dist[j]);
//
printf("%d\n",j );
for(Vertex W=0;WNv;W++)//对邻接点dist进行更新操作
if(Graph->G[j][W]!=INFINITY&&dist[W]>dist[j]+Graph->G[j][W]&&U[W]==false)
{dist[W]=dist[j]+Graph->G[j][W];path[W]=j;}
}
}
int main(){
MGraph Graph=BuildGraph();
Dijkstra(Graph,0);
return 0;
}
下一篇多源最短路径