如何让Bert在finetune小数据集时更“稳”一点
作者:邱震宇(华泰证券股份有限公司 算法工程师)
知乎专栏:我的ai之路
来自:AINLP
最近刷到一篇论文,题目是Revisiting Few-sample BERT Fine-tuning 。论文刚挂到arxiv上,虽然关注的人还不是很多,但是读完之后发现内容很实用,很适合应用到实际的业务中。本文主要就这篇论文中的一些观点进行解读和实验验证。
话不多说,直接进入正题。这篇论文主要探讨的主题是如何更有效地使用bert在小数据集上进行finetune。论文指出目前bert的finetune存在不稳定的问题,尤其是在小数据集上,训练初期,模型会持续震荡,进而会降低整个训练过程的效率,减慢收敛的速度,也会在一定程度上降低模型的精度。文章主要总结了三个优化的方向,分别从优化方法、权重参数、训练方式等角度探讨了如何在小数据集上稳定finetune bert模型。下面将分别从这三个的角度详细解读。
Adam优化的debiasing
不知道大家在使用tensorflow或者pytorch版本的官方bert源码时,有没有发现他们的Adam实现源码与原版的Adam实现略有不同。我们先来简单回顾一下Adam算法的流程:

adam主要是结合了一阶动量、二阶动量滑动平均,并辅以learning rate的adaptive change,使得模型训练能够更加高效且能够自适应改变learning rate。除此之外,adam还有一个算法细节需要关注,即bias correcting。注意到上图中红色框标注的部分,在梯度更新操作之前,需要对一阶动量和二阶动量进行bias修正。这样做的原因在于adam的动量均是使用0来初始化。因此在模型训练初期以及指数衰减率超参数( )很小的时候,动量估计值很容易往0的方向偏移,此时需要对动量做偏移修正,具体的修正操作如图红色框所示。具体的推导可以参考原始的Adam论文。这里简单回顾一下,以二阶动量的推导为例:
推导的主要逻辑在于建立二阶动量 的期望 与 的期望 的表达式关系。
首先根据上图的步骤8,可以将二阶动量 转化为以历史时间戳上的梯度 为变量的函数:
对上式两边同时求期望,可以得到:
(updated on 2020.06.17)新增内容:这里的推导我又研究了一下,最后看到一个网站上的回答有些道理,这里贴出来供大家参考:Understanding a derivation of bias correction for the Adam optimizer
首先要弄清楚 是怎么得到的。推测 是根据当前时刻的梯度 去估计历史梯度 时的误差项。有了这个误差项,我们就可以将 项从求和公式中移出来,不再依赖i。而所有包含 的项此时可以看成是常量,可以从期望的括号中移出来。当二阶动量是一个稳态分布时,在每个时刻t上它都是一个常量,因此 为0。
那么接下来还有一个问题就是 如何化简为 的呢?这就需要用到有限等比数列求和的相关公式了。对于一个有限等比数列,它的求和可以表达为如下公式:
自我吐槽一下:高中数学全还给老师了,汗颜。。。
此时将 带入上式,同时由于我们已经将当前时刻的 从求和公式中提了出来,因此可以做出如下推导:
上述第二项等式通过将 乘到右边的除法项,同时分子分母同时乘以 就可以得到第三项。
其中, 可以通过控制衰减率超参数 ,来让其接近于0。那么剩下的偏移影响因素就是 。因此,我们通过将 除以这个项来达到偏移修正的目的。
这块推导由于本人数学能力不强,所以理解得不是很深入,欢迎数学不错的同学前来拍砖。
Bert的adam
我们查看google给出的官方bert源码工程(github.com/google-resea)中的optimization.py,在其AdamWeightDecay类中,可以看到其省略了上述偏移修正的步骤:
m = tf.get_variable(
name=param_name + "/adam_m",
shape=param.shape.as_list(),
dtype=tf.float32,
trainable=False,
initializer=tf.zeros_initializer())
v = tf.get_variable(
name=param_name + "/adam_v",
shape=param.shape.as_list(),
dtype=tf.float32,
trainable=False,
initializer=tf.zeros_initializer())
# Standard Adam update.
next_m = (
tf.multiply(self.beta_1, m) + tf.multiply(1.0 - self.beta_1, grad))
next_v = (
tf.multiply(self.beta_2, v) + tf.multiply(1.0 - self.beta_2,
tf.square(grad)))
update = next_m / (tf.sqrt(next_v) + self.epsilon)通过查阅Bert的原始论文,并没有发现作者在这块有具体的说明,只能推测使用bert做预训练时,由于训练语料规模非常庞大,且训练的步数也是非常多,因此即使不做偏移修正,模型仍然能够在训练过程中慢慢保持稳定状态,且减去了偏移修正的计算量,整体的计算成本还降低了一些。
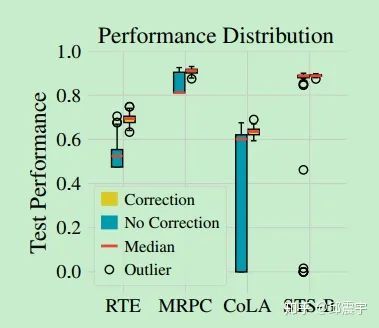
然而,如果在样本较少的下游任务场景下,仍然使用这种优化方式就会出现训练不稳定的问题。为了验证这个结论,论文作者做了细致的比对实验,他们在四个不同的数据集上,尝试了50种不同的随机种子,分别用带偏移修正的原始adam和不带修正的bertAdam去做finetune任务。实验结果分别从不同角度来验证上述的观点,比如下图:
这是一个模型在不同数据集上的测试集效果箱线图,图中表明在四个数据集上,使用偏移修正的adam能够极大提升模型在测试集上的效果。
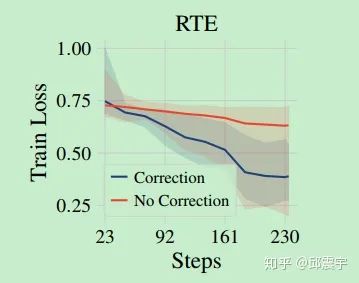
再看下面这个图:
这张图反映了模型在小数据集RTE上的训练曲线。可以看到,使用偏移修正的Adam来finetune能够更快达到收敛,同时获得更小的loss。
再次验证
实践出真知,为了验证上述结论的有效性,我决定找一个小数据集进行实际测试。正好最近有一个ccks举办的实体识别比赛,名称是面向试验鉴定的命名实体识别任务。这个比赛的训练样本只有400条,实体类型有4种,足以称得上是小数据量了,正好可以拿来做实验。实验的模型主体是Bert+crf框架,超参数和随机种子都固定不变,唯一改变条件的就是是否使用偏移修正。
(updated on 2020.06.17)在tf的bert实现中,要将原始的偏移修正补充进去,要添加一定量的代码,主要是增加 的计算和更新,以及偏移修正的逻辑计算。通过阅读原始的tf的adam源码,可以发现它的偏移修正是通过对learning_rate进行修正,即 。除此之外,tensorflow还对的更新和赋值有自己的计算图优化逻辑,所以相比较于keras的代码更为复杂。下面贴出补充完误差修正后的adamweightdecay代码,可与原始的adam代码对比查看:
class AdamWeightDecayOptimizer(optimizer.Optimizer):
"""A basic Adam optimizer that includes "correct" L2 weight decay."""
def __init__(self,
learning_rate,
weight_decay_rate=0.0,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-6,
exclude_from_weight_decay=None,
name="AdamWeightDecayOptimizer"):
"""Constructs a AdamWeightDecayOptimizer."""
super(AdamWeightDecayOptimizer, self).__init__(False, name)
self.learning_rate = learning_rate
self.weight_decay_rate = weight_decay_rate
self.beta_1 = beta_1
self.beta_2 = beta_2
self.epsilon = epsilon
self.exclude_from_weight_decay = exclude_from_weight_decay
self.learning_rate_t = None
self._beta1_t = None
self._beta2_t = None
self._epsilon_t = None
def _get_beta_accumulators(self):
with ops.init_scope():
if context.executing_eagerly():
graph = None
else:
graph = ops.get_default_graph()
return (self._get_non_slot_variable("beta1_power", graph=graph),
self._get_non_slot_variable("beta2_power", graph=graph))
def _prepare(self):
self.learning_rate_t = ops.convert_to_tensor(
self.learning_rate, name='learning_rate')
self.weight_decay_rate_t = ops.convert_to_tensor(
self.weight_decay_rate, name='weight_decay_rate')
self.beta_1_t = ops.convert_to_tensor(self.beta_1, name='beta_1')
self.beta_2_t = ops.convert_to_tensor(self.beta_2, name='beta_2')
self.epsilon_t = ops.convert_to_tensor(self.epsilon, name='epsilon')
def _create_slots(self, var_list):
first_var = min(var_list, key=lambda x: x.name)
self._create_non_slot_variable(initial_value=self.beta_1,
name="beta1_power",
colocate_with=first_var)
self._create_non_slot_variable(initial_value=self.beta_2,
name="beta2_power",
colocate_with=first_var)
for v in var_list:
self._zeros_slot(v, 'm', self._name)
self._zeros_slot(v, 'v', self._name)
def _apply_dense(self, grad, var):
learning_rate_t = math_ops.cast(
self.learning_rate_t, var.dtype.base_dtype)
beta_1_t = math_ops.cast(self.beta_1_t, var.dtype.base_dtype)
beta_2_t = math_ops.cast(self.beta_2_t, var.dtype.base_dtype)
epsilon_t = math_ops.cast(self.epsilon_t, var.dtype.base_dtype)
weight_decay_rate_t = math_ops.cast(
self.weight_decay_rate_t, var.dtype.base_dtype)
m = self.get_slot(var, 'm')
v = self.get_slot(var, 'v')
beta1_power, beta2_power = self._get_beta_accumulators()
beta1_power = math_ops.cast(beta1_power, var.dtype.base_dtype)
beta2_power = math_ops.cast(beta2_power, var.dtype.base_dtype)
learning_rate_t = math_ops.cast(self.learning_rate_t, var.dtype.base_dtype)
learning_rate_t = (learning_rate_t * math_ops.sqrt(1 - beta2_power) / (1 - beta1_power))
# Standard Adam update.
next_m = (
tf.multiply(beta_1_t, m) +
tf.multiply(1.0 - beta_1_t, grad))
next_v = (
tf.multiply(beta_2_t, v) + tf.multiply(1.0 - beta_2_t,
tf.square(grad)))
update = next_m / (tf.sqrt(next_v) + epsilon_t)
if self._do_use_weight_decay(var.name):
update += weight_decay_rate_t * var
update_with_lr = learning_rate_t * update
next_param = var - update_with_lr
return control_flow_ops.group(*[var.assign(next_param),
m.assign(next_m),
v.assign(next_v)])
def _resource_apply_dense(self, grad, var):
learning_rate_t = math_ops.cast(
self.learning_rate_t, var.dtype.base_dtype)
beta_1_t = math_ops.cast(self.beta_1_t, var.dtype.base_dtype)
beta_2_t = math_ops.cast(self.beta_2_t, var.dtype.base_dtype)
epsilon_t = math_ops.cast(self.epsilon_t, var.dtype.base_dtype)
weight_decay_rate_t = math_ops.cast(
self.weight_decay_rate_t, var.dtype.base_dtype)
m = self.get_slot(var, 'm')
v = self.get_slot(var, 'v')
beta1_power, beta2_power = self._get_beta_accumulators()
beta1_power = math_ops.cast(beta1_power, var.dtype.base_dtype)
beta2_power = math_ops.cast(beta2_power, var.dtype.base_dtype)
learning_rate_t = math_ops.cast(self.learning_rate_t, var.dtype.base_dtype)
learning_rate_t = (learning_rate_t * math_ops.sqrt(1 - beta2_power) / (1 - beta1_power))
# Standard Adam update.
next_m = (
tf.multiply(beta_1_t, m) +
tf.multiply(1.0 - beta_1_t, grad))
next_v = (
tf.multiply(beta_2_t, v) + tf.multiply(1.0 - beta_2_t,
tf.square(grad)))
update = next_m / (tf.sqrt(next_v) + epsilon_t)
if self._do_use_weight_decay(var.name):
update += weight_decay_rate_t * var
update_with_lr = learning_rate_t * update
next_param = var - update_with_lr
return control_flow_ops.group(*[var.assign(next_param),
m.assign(next_m),
v.assign(next_v)])
def _apply_sparse_shared(self, grad, var, indices, scatter_add):
learning_rate_t = math_ops.cast(
self.learning_rate_t, var.dtype.base_dtype)
beta_1_t = math_ops.cast(self.beta_1_t, var.dtype.base_dtype)
beta_2_t = math_ops.cast(self.beta_2_t, var.dtype.base_dtype)
epsilon_t = math_ops.cast(self.epsilon_t, var.dtype.base_dtype)
weight_decay_rate_t = math_ops.cast(
self.weight_decay_rate_t, var.dtype.base_dtype)
m = self.get_slot(var, 'm')
v = self.get_slot(var, 'v')
beta1_power, beta2_power = self._get_beta_accumulators()
beta1_power = math_ops.cast(beta1_power, var.dtype.base_dtype)
beta2_power = math_ops.cast(beta2_power, var.dtype.base_dtype)
learning_rate_t = math_ops.cast(self.learning_rate_t, var.dtype.base_dtype)
learning_rate_t = (learning_rate_t * math_ops.sqrt(1 - beta2_power) / (1 - beta1_power))
m_t = state_ops.assign(m, m * beta_1_t,
use_locking=self._use_locking)
m_scaled_g_values = grad * (1 - beta_1_t)
with ops.control_dependencies([m_t]):
m_t = scatter_add(m, indices, m_scaled_g_values)
v_scaled_g_values = (grad * grad) * (1 - beta_2_t)
v_t = state_ops.assign(v, v * beta_2_t, use_locking=self._use_locking)
with ops.control_dependencies([v_t]):
v_t = scatter_add(v, indices, v_scaled_g_values)
update = m_t / (math_ops.sqrt(v_t) + epsilon_t)
if self._do_use_weight_decay(var.name):
update += weight_decay_rate_t * var
update_with_lr = learning_rate_t * update
var_update = state_ops.assign_sub(var,
update_with_lr,
use_locking=self._use_locking)
return control_flow_ops.group(*[var_update, m_t, v_t])
def _apply_sparse(self, grad, var):
return self._apply_sparse_shared(
grad.values, var, grad.indices,
lambda x, i, v: state_ops.scatter_add( # pylint: disable=g-long-lambda
x, i, v, use_locking=self._use_locking))
def _resource_scatter_add(self, x, i, v):
with ops.control_dependencies(
[resource_variable_ops.resource_scatter_add(
x.handle, i, v)]):
return x.value()
def _resource_apply_sparse(self, grad, var, indices):
return self._apply_sparse_shared(
grad, var, indices, self._resource_scatter_add)
def _do_use_weight_decay(self, param_name):
"""Whether to use L2 weight decay for `param_name`."""
if not self.weight_decay_rate:
return False
if self.exclude_from_weight_decay:
for r in self.exclude_from_weight_decay:
if re.search(r, param_name) is not None:
return False
return True
def _finish(self, update_ops, name_scope):
# Update the power accumulators.
with ops.control_dependencies(update_ops):
beta1_power, beta2_power = self._get_beta_accumulators()
with ops.colocate_with(beta1_power):
update_beta1 = beta1_power.assign(
beta1_power * self.beta_1_t, use_locking=self._use_locking)
update_beta2 = beta2_power.assign(
beta2_power * self.beta_2_t, use_locking=self._use_locking)
return control_flow_ops.group(*update_ops + [update_beta1, update_beta2],
name=name_scope)主要关注_get_beta_accumulators,_finish,以及在各个_apply_方法中进行偏移修正的计算逻辑:
beta1_power, beta2_power = self._get_beta_accumulators()
beta1_power = math_ops.cast(beta1_power, var.dtype.base_dtype)
beta2_power = math_ops.cast(beta2_power, var.dtype.base_dtype)
learning_rate_t = math_ops.cast(self.learning_rate_t, var.dtype.base_dtype)
learning_rate_t = (learning_rate_t * math_ops.sqrt(1 - beta2_power) / (1 - beta1_power))最后,根据实验结果,验证了上述结论的有效性。通过使用误差修正,模型训练效率显著提升,只用了一半的训练步数就达到了未用误差修正的训练loss,相当于加快了收敛的速度。最终模型的精度也有小幅的提升。
这里提一下苏神的bert4keras框架中,很早就注意到了误差修正这个问题,增加了误差修正的选项和步骤,有兴趣的同学可以去研究一下该框架。建议对adam理解不深入的同学阅读苏神的代码,很简洁易懂,而tf中的源码为了优化图计算写了很多复杂代码。
Weight Re-initializing
论文提到的第二个优化点是权重再初始化。我们使用bert做finetune时,通常会使用bert的预训练权重去初始化下游任务中的模型参数,这样做是为了充分利用bert在预训练过程中学习到的语言知识,将其能够迁移到下游任务的学习当中。众所周知,bert主要由很多transformer层堆叠构成,那么问题来了,是否所有的transformer层都对下游任务有帮助呢?
之前有一些论文专门讨论了bert中不同层的权重分别学习到了哪些信息,大致思想是靠近底部的层(靠近input)学到的是比较通用的语义方面的信息,比如词性、词法等语言学知识,而靠近顶部的层会倾向于学习到接近下游任务的知识,对于预训练来说就是类似masked word prediction、next sentence prediction任务的相关知识。当使用bert预训练模型finetune其他下游任务(比如序列标注)时,如果下游任务与预训练任务差异较大,那么bert顶层的权重所拥有的知识反而会拖累整体的finetune进程,使得模型在finetune初期产生训练不稳定的问题。
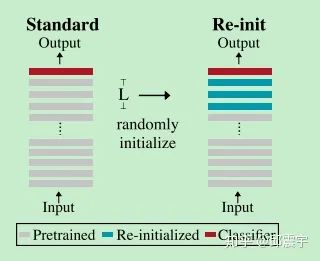
因此,我们可以在finetune时,只保留接近底部的bert权重,对于靠近顶部的层的权重,可以重新随机初始化,从头开始学习。论文做了如下实验来验证上述结论:重新初始化bert的pooler层(文本分类会用到),同时尝试重新初始化bert的top-L层权重, 。该超参数可以使用交叉验证法来调整。具体步骤和实验结果如图所示:

根据上述实验结果,在四个数据集上,模型通过重新初始化部分权重,在精度上都有不同程度的提升。另外,作者还做了一个实验验证到底该对多少层的权重进行重新初始化。实验结果表明这个并没有显著规律,实际上初始化层数与具体的任务和数据集相关的,需要通过调参来决定。但是有一点是可以肯定的,对于需要用到pooler层的分类任务,对pooler层进行重新初始化肯定能对模型的训练有一定的帮助。
再次验证
同样的,我也在ccks的实体识别比赛中验证了上述的想法。通过固定其他参数(包括不使用偏移修正的Adam),我对bert的前6层进行了重新初始化,具体代码实现只需要在modeling.py中的get_assignment_map_from_checkpoint方法中,将需要重新初始化的权重层参数从assignment_map中过滤掉就可以了,具体如下:
def get_assignment_map_from_checkpoint(tvars, init_checkpoint):
"""Compute the union of the current variables and checkpoint variables."""
assignment_map = {}
initialized_variable_names = {}
name_to_variable = collections.OrderedDict()
for var in tvars:
name = var.name
m = re.match("^(.*):\\d+$", name)
if m is not None:
name = m.group(1)
name_to_variable[name] = var
init_vars = tf.train.list_variables(init_checkpoint)
assignment_map = collections.OrderedDict()
filtered_layer_names = [......] //这里放需要重新初始化的权重参数名称就可以了
for x in init_vars:
(name, var) = (x[0], x[1])
if name not in name_to_variable:
continue
if name not in filtered_layer_names:
assignment_map[name] = name_to_variable[name]
initialized_variable_names[name] = 1
initialized_variable_names[name + ":0"] = 1
return (assignment_map, initialized_variable_names)通过实验,验证了上述的结论。将bert顶部的6层权重重新初始化后,模型的训练效率有了较大提升,收敛速度加快了30-40%,然而最后模型的精度似乎没有太大的变化,应该还是需要根据验证集来调整最合适的重新初始化层数,才能达到精度的提升。
用更长的步数来finetune
这块优化内容我感觉似乎没有太大的亮点。作者的意思是通过增加训练步数能够提升finetune的效果。但是一般我都是用early-stopping机制来控制训练的步数,因此感觉这块内容帮助不大,这里我就不过多介绍了。
更多对比实验
论文在最后还做了一组对比实验,他将目前几个比较经典的解决训练震荡的方法列了出来,具体如下:
1、Pre-trained Weight Decay,传统的weight decay中,权重参数会减去一个正则项 。而pre-trained weight decay则是在finetune时,将预训练时的权重 引入到weight decay计算中 ,最终正则项为 。通过这种方式,能够使得模型的训练变得更稳定。
2、Mixout。在finetune时,每个训练iter都会设定给一个概率p,模型会根据这个p将模型参数随机替换成预训练的权重参数。这个方法主要是为了减缓灾难性遗忘,让模型不至于在finetune任务时忘记预训练时学习到的知识。
3、Layerwise Learning Rate Decay。这个方法我也经常会去尝试,即对于不同的层数,会使用不同的学习率。因为靠近底部的层学习到的是比较通用的知识,所以在finetune时并不需要它过多的去更新参数,相反靠近顶部的层由于偏向学习下游任务的相关知识,因此需要更多得被更新。
4、Transferring via an Intermediate Task。即在finetune一个小样本数据集任务时,先在一个较大的过渡任务上进行finetune。
作者将上述四个方法与本论文中的几个优化点做了对比实验,最后发现相对于只使用偏移修正的Adam优化算法,Pre-trained Weight Decay、Mixout、Layerwise Learning Rate Decay并没有显著的优势。当结合了偏移修正和权重重新初始化之后,上述三个方法的效果是明显有差距的。而对于Transferring via an Intermediate Task,虽然它的效果很好,但是它需要额外的标注数据,成本比较高。而且我自己也做了一些验证测试,我使用了MSRA的中文NER数据集先做了finetune,然后再用其权重参数尝试了ccks的NER任务,结果并没有得到明显的提升,个人认为这个过度任务可能需要与目标任务的领域有一定的相关性,不然还需要做领域迁移的工作。
小结
本文主要解读了论文Revisiting Few-sample BERT Fine-tuning。通过深入研究bert在finetune小样本数据集时遇到的训练不稳定问题,提出了几个优化方法,包括使用带偏移修正的adam优化方法、重新初始化部分权重参数等。作者做了详尽的实验来验证上述方法,同时本人也在一个小样本任务上做了简单的二次验证,最终证明上述方法是有效的。由于上述方法操作非常简便,对原始的代码改动很少,因此非常适合应用于实际的项目中。
添加个人微信,备注:昵称-学校(公司)-方向,即可获得
1. 快速学习深度学习五件套资料
2. 进入高手如云DL&NLP交流群
![]()
记得备注呦
![]()