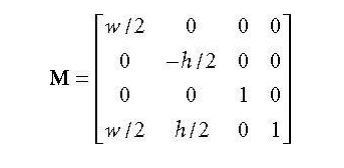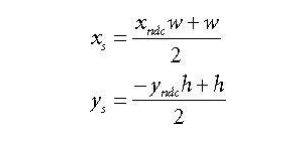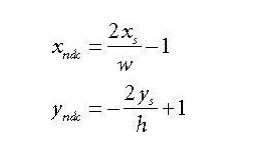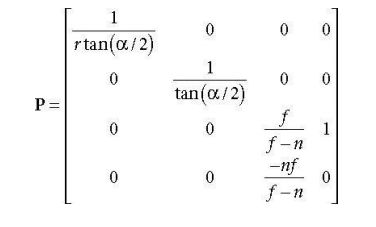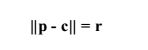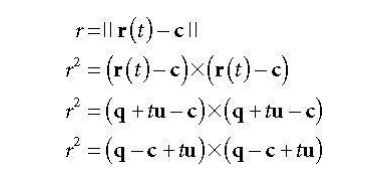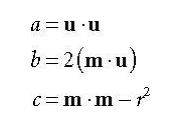Directx11教程三十八之Pick(拾取技术)

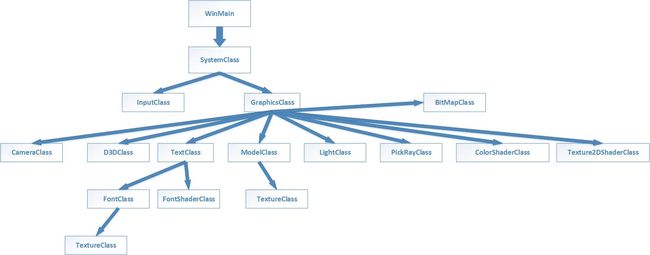
这节教程是关于Pick(拾取技术的),程序的结构如下:

在看这节教程前先弄懂：(1)大概了解D3D11的渲染流水线

                                            (2)      D3D11教程三十七之FrustumCulling(视截体裁剪)上半节教程， 弄不懂也没关系，两节教程之间有一些联系，但是由于我们的教程简化模型，就算看不懂D3D11教程三十七之FrustumCulling(视截体裁剪)上半节教程也不影响这节教程的理解。

一，Pick技术的简介。

Pick技术简单的来描述，其实就是在一个编辑器或者3D程序界面中，通过鼠标的点击来选取一个3D物体。我这里拿出虚幻四游戏引擎来做示例，看下面图：

上面就是大名鼎鼎的虚幻四游戏引擎的编辑界面了，里面高亮的石头就是通过点击鼠标来选取的，下面我就讲解一下这种拾取技术的原理。

二，Pick技术的原理。

我们在界面通过鼠标点击，具体的点击3D物体的过程如下面所示：在相机空间发出以相机原点发出的射线与位于相机空间的3D物体相交(本节教程的3D物体为球体)

  由于此时鼠标是位于Win32屏幕空间的，一般情况上(有时间不一定，仅仅是一般情况下)win32屏幕空间的左上角为原点，为二维坐标， 如下面图所示：

假设屏幕宽为ScreenWidth,高为ScreenHieght,  则鼠标点击在win32窗口坐标空间的坐标为(x,y),则x和y的范围是：   

0=

从3D渲染管线图 我们大概知道：顶点从相机空间到win32窗口坐标空间有三次变换

一，透视投影变换,即乘以透视投影矩阵,(这一步发生在相机空间)

二，透视除法,除以w(这一步发生在齐次裁剪空间)

三，视口变换,即乘以视口变换矩阵(这一步发生在NDC空间)

所以我们想让顶点坐标从win32坐标空间变换到相机空间，得逆过来计算

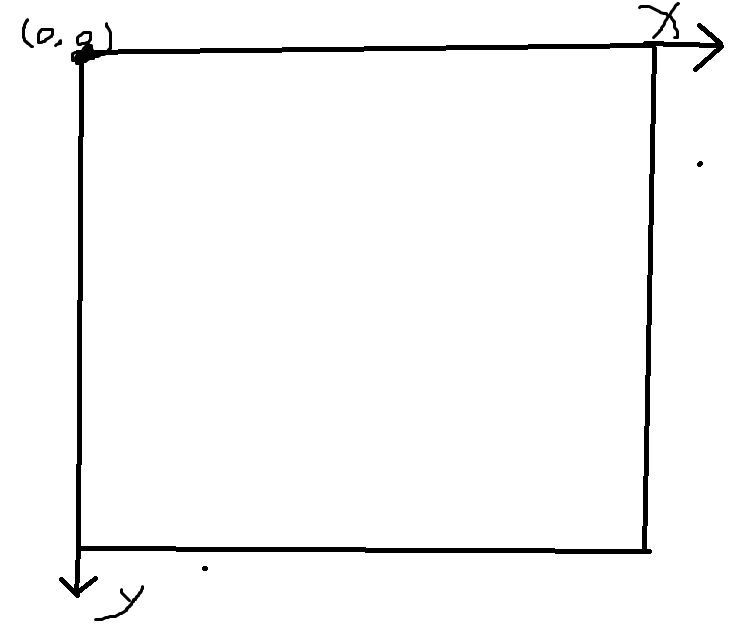
一，从win32坐标空间(屏幕空间)变换到NDC坐标

在NDC空间的顶点乘以视口变换矩阵变换到屏幕空间，所以先来看看视口变换矩阵,

看上面, 窗口的宽度为Width,窗口高度为Height,TopLeftX为窗口左上角顶点X值，TopLeftY为窗口左上角顶点Y值，MaxDepth为深度缓存的最大值，MinDepth为深度缓存的最小值，我们上面说过，一般情况下win32坐标空间的左手角为原点(0,0),所以TopLeftX=0，TopLeftY=0，而一般情况 MaxDepth=1.0, MinDepth=0.0,因此视口变换矩阵可以简化为:

假设在NDC空间的坐标为( xndc, yndc, zndc,1.0f),注意在NDC空间中 -1=< xndc<=1,  -1=< yndc,<=1,  0=< zndc=1,详情请见上面的D3D11渲染管线图.

从NDC空间变换到屏幕空间如下面所示：

假设屏幕空间上的顶点坐标为 ( x s, y s),则满足下面的关系式子：

我们上面说过得逆过来计算，也就是由屏幕空间的顶点坐标 ( x s, y s),得到NDC空间的顶点坐标得到( xndc, yndc, zndc,1.0f),如下面所示:

                        公式(1)

我们同学可能还有疑问？ zndc为什么呢?其实很简单，我们说过0.0=

这样顶点就从屏幕空间变换到NDC空间了

二，从NDC坐标变换到齐次裁剪空间。

在齐次裁剪空间的顶点进行透视除法变换到NDC空间，在齐次裁剪空间中坐标为( Xh, Yh, Zh, Wh),  注意   - Wh=< Xh<= Wh,   - Wh=< Yh<= Wh,  0=< Zh<= Wh.

透视除法过程为:                        xndc= Xh/ Wh; 

                                                    yndc= Yh/ Wh;

                                                    zndc= Zh/ Wh;

                                                    wndc=1.0= Wh/ Wh;

那么 Wh是什么呢？ Wh为相机空间的顶点坐标的Z值，详情见上面的D3D11渲染管线图。而在我们的Pick技术里，点击的顶点恰恰是屏幕上的顶点，并且屏幕空间恰恰是相机空间的近截面，所以 Wh=n,( 这里假设Z=n为相机空间的近截面，Z=f为相机空间的远截面),。

即  透视除法具体过程为               xndc= Xh/ n;         

                                   yndc= Yh/ n;         

                                  zndc= Zh/ n;     

                                                      wndc=1.0= n/ n;

逆过来求就是：

Xh=Xndc*n;     Yh=Yndc*n;                Zh=Zndc*n=0*n=0;         Wn=Wndc*n=1.0*n=n;

联立公式1： Xndc=2*Xs/w-1           Yndc=-2*Ys/h+1

可得：

Xh=(2*Xs/w-1)*n        Yh=(-2*Ys/h+1)*n       Zh=0      Wh=n

                              

                                            公式(2)

三，从齐次裁剪空间到相机空间。

在相机空间的顶点乘以透视投影矩阵变换到齐次裁剪空间，所以先来看看D3D11的透视投影矩阵

也就是

上面这里A和B的引进仅仅是为了方便表示而已， 其中A=f/(f-n)     B=-nf/(f-n), 而上面我们假设过相机空间的近截面为Z=n,  远截面为Z=f,  而 r为屏幕的宽高比， α为视截体在YZ平面投影的FOV角大小，如下面所示：

我们顶点(Xv,Yv,Zv,1.0f);从相机空间乘以透视投影矩阵而变换到齐次裁剪空间，用下面公式表示：

那么由齐次裁剪空间顶点坐标( Xh, Yh, Zh, Wh)算出相机空间的(Xv,Yv,Zv,1.0f)，由上面可以知道

                                 Xh=Xv/(r*tan(α/2))

                           Yh=Yv/tan(α/2)

                           Zh=Zv*A+B

                           Wh=Zv

 

逆过来求则得到：

                          Xv=Xh*(r*tan(α/2))

                          Yv=Yh*tan(α/2)

                          Zv=(Zh-B)/A

                          Wv=1.0f;

联立上面的公式3，Xh=(2*Xs/w-1)*n        Yh=(-2*Ys/h+1)*n       Zh=0      Wh=n

得到

Xv={(2*Xs/w-1)*n }*{(r*tan( α / 2 ))}={(2*Xs/w-1)*n }/{(1/(r*tan(α/2)))}

Yv=Yh*tan(α/2)={(-2*Ys/h+1)*n}/{1/(tan(α/2))}

Zv=-B/A={nf/(f-n)}/{f/(n-f)}=n

Wv=1.0f

当然我们求出相机空间再近截面的点并不需要直接用到r, α这两个变量,我们可以直接借用透视投影矩阵，假设透视投影矩阵为ProjMa,   则ProjMa11=1/(r*tan(α/2)),        ProjMa22=tan(α/2),注意这里下标从1开始，而非0开始

最后得到

Xv={(2*Xs/w-1)*n }/ProjMa11;

Yv={(-2*Ys/h+1)*n}/ProjMa22;

Zv=n

Wv=1.0f

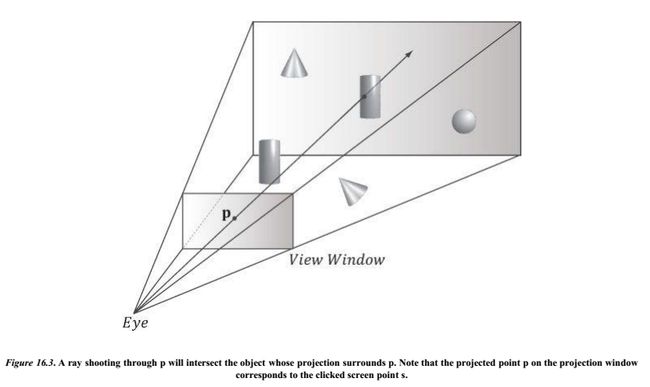
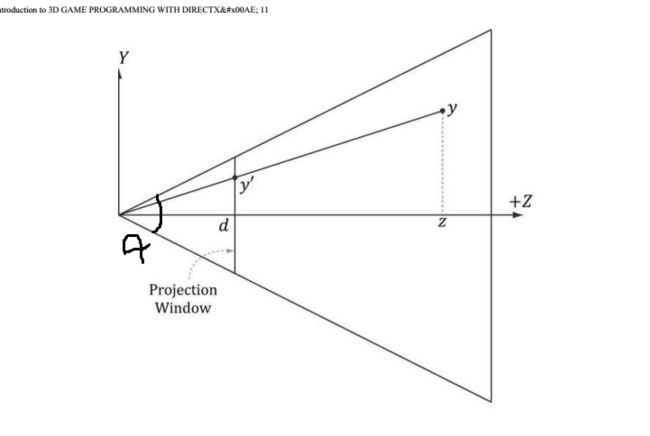
这次再次放出前面已经出现过一次的一张图：

上面P点在屏幕空间坐标就是(Xs,Ys),在相机空间坐标就是(Xv,Yv,Zv,1.0f),射线AB是从点Eye出发经过P点的射线，在相机空间中点Eye(相机)处在原点(0,0,0,1.0f)

射线向量为P-Eye=( {(2*Xs/w-1)*n }/ ProjMa11,{(-2*Ys/h+1)*n}/ProjMa22,n,0);

把公约数n除掉，得到射线向量   ( (2*Xs/w-1) / ProjMa11,(-2*Ys/h+1)/ProjMa22,1.0f,0);

最终相机空间的射线用两个量表示：     射线原点RayOrigin(0,0,0,1.0f) 

                                          射线向量   ((2*Xs/w-1) /ProjMa11,(-2*Ys/h+1)/ProjMa22,1.0f,0)

所以说关于这的推导有些地方不太对的

计算相机空间的射线代码如下：

bool PickRayClass::Frame(int mouseX, int mouseY)
{
	//计算在相机空间的射线
	float vx = (2.0f*(float)mouseX / mScreenWidth - 1.0f) / mProjMatrix._11;
	float vy = (-2.0f*(float)mouseY / mScreenHeight + 1.0f) / mProjMatrix._22;

	mViewSpaceRayOrigin = XMFLOAT4(0.0f, 0.0f, 0.0f, 1.0f);
	mViewSpaceRayDir = XMFLOAT3(vx, vy, 1.0f); //是单位向量?

	return true;
}

从上面我们计算出了相机空间的射线，但是我们为了方便的计算球体和射线的相交以及某些其它原因(限于篇幅，不讲了)，我们直接将射线从相机空间直接变换到球体的局部空间

代码如下：

       XMMATRIX ViewMatrix, InvViewMatrix,WorldMatrix,InvWorldMatrix;

	XMVECTOR mLocalSpaceRayOrigin;
	XMVECTOR mLocalSpaceRayRayDir;

	//更新相机矩阵
	mCamera->Render();

	//获取相机矩阵和世界矩阵
	ViewMatrix = mCamera->GetViewMatrix();
	WorldMatrix = mD3D->GetWorldMatrix()*XMMatrixTranslation(SpherePosX, SpherePosY, SpherePosZ);

	//获取相机矩阵的逆矩阵和世界矩阵的逆矩阵
	InvViewMatrix = XMMatrixInverse(&XMMatrixDeterminant(ViewMatrix), ViewMatrix);
	InvWorldMatrix = XMMatrixInverse(&XMMatrixDeterminant(WorldMatrix), WorldMatrix);

	//将相机矩阵的逆矩阵与世界矩阵的逆矩阵相乘,得注意相机逆矩阵在前，世界逆矩阵在后
	XMMATRIX InvMa = XMMatrixMultiply(InvViewMatrix, InvWorldMatrix);

	//将射线的原点和方向向量从相机空间变到局部空间，局部空间物体的中心为(0.0f,0.0f,0.0f)
	mLocalSpaceRayOrigin = XMVector3TransformCoord(ViewSpaceRayOrigin,InvMa);

	mLocalSpaceRayRayDir = XMVector3TransformNormal(ViewSpaceRayDir, InvMa);
	mLocalSpaceRayRayDir = XMVector3Normalize(mLocalSpaceRayRayDir);

注意这两个函数的使用：
XMVector3TransformNormal变换XMVECTOR时，变换XMVECTOR时，把向量的第四个分量W看作为0.0，也就是真正的向量。

XMVector3TransformCoord变换XMVECTOR时,  变换XMVECTOR时，把向量的第四个分量W看作为1.0，也就是真正的点。

三，计算球体和射线的相交.

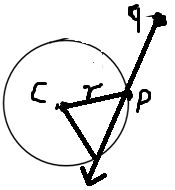
假设球体和射线处于同一个空间，q为射线的原点，u为射线的射线向量,则射线上面的点可以用 r(t)=q+t*u 表示，注意t为标量

假设C点为球体的圆心，r为球体的半径：

假设射线与球体相交，交点为P，如图所示：

我们知道射线与球的交点P位于球上，P到球心C的距离为半径r, 则得出等式：

而P是射线上的点，P=r(t)= q+t*u,  t为某个实数

令 m=q-c,则

我们又回到了初中时代的一元二次方程式的求解问题，下面得到各个系数：

我们拿出初中方程的判定解数量的方程式：

△=b*b-4*a*c

(1)如果△=0 则线段和球体有且仅有一个交点

(2) 如果△<0,则线段和球体无交点

(3) 如果△>0,则线段和球体有两个不同的交点

所以当△>=0时，我们的线段和球体就存在交点，其实我想过一个问题，存在射线反向与球体相交，而射线正向不与球体相交的情况，毕竟线段和射线是有区别的，这个留给读者思考，我们在本节教程就假设△>=0时，射线和球体相交。

代码实现(球体球心坐标和射线必须在同一个空间，我的实例代码是在物体球体的局部空间的)：

	float a, b, c,discriminant; //二次方程式系数和判别式
	XMFLOAT3 m;
	XMFLOAT3 dir;
	XMStoreFloat3(&m, mLocalSpaceRayOrigin);
	XMStoreFloat3(&dir, mLocalSpaceRayRayDir);

	a = dir.x*dir.x + dir.y*dir.y + dir.z*dir.z; //a>0 二次系数为正 
	b = 2 * (m.x*dir.x + m.y*dir.y + m.z*dir.z);
	c = (m.x*m.x + m.y*m.y + m.z*m.z)-radius*radius;
	discriminant = b*b - 4 * a*c;

跟上面计算局部空间的射线那段代码一起放在一个函数：

bool GraphicsClass::TestIntersection(FXMVECTOR ViewSpaceRayOrigin, FXMVECTOR ViewSpaceRayDir, float SpherePosX, float SpherePosY, float SpherePosZ, float radius)
{
	XMMATRIX ViewMatrix, InvViewMatrix,WorldMatrix,InvWorldMatrix;

	XMVECTOR mLocalSpaceRayOrigin;
	XMVECTOR mLocalSpaceRayRayDir;

	//更新相机矩阵
	mCamera->Render();

	//获取相机矩阵和世界矩阵
	ViewMatrix = mCamera->GetViewMatrix();
	WorldMatrix = mD3D->GetWorldMatrix()*XMMatrixTranslation(SpherePosX, SpherePosY, SpherePosZ);

	//获取相机矩阵的逆矩阵和世界矩阵的逆矩阵
	InvViewMatrix = XMMatrixInverse(&XMMatrixDeterminant(ViewMatrix), ViewMatrix);
	InvWorldMatrix = XMMatrixInverse(&XMMatrixDeterminant(WorldMatrix), WorldMatrix);

	//将相机矩阵的逆矩阵与世界矩阵的逆矩阵相乘,得注意相机逆矩阵在前，世界逆矩阵在后
	XMMATRIX InvMa = XMMatrixMultiply(InvViewMatrix, InvWorldMatrix);

	//将射线的原点和方向向量从相机空间变到局部空间，局部空间物体的中心为(0.0f,0.0f,0.0f)
	mLocalSpaceRayOrigin = XMVector3TransformCoord(ViewSpaceRayOrigin,InvMa);

	mLocalSpaceRayRayDir = XMVector3TransformNormal(ViewSpaceRayDir, InvMa);
	mLocalSpaceRayRayDir = XMVector3Normalize(mLocalSpaceRayRayDir);

	//下面计算世界空间，射线是否与球体相交
	float a, b, c,discriminant; //二次方程式系数和判别式
	XMFLOAT3 m;
	XMFLOAT3 dir;
	XMStoreFloat3(&m, mLocalSpaceRayOrigin);
	XMStoreFloat3(&dir, mLocalSpaceRayRayDir);

	a = dir.x*dir.x + dir.y*dir.y + dir.z*dir.z; //a>0 二次系数为正 
	b = 2 * (m.x*dir.x + m.y*dir.y + m.z*dir.z);
	c = (m.x*m.x + m.y*m.y + m.z*m.z)-radius*radius;
	discriminant = b*b - 4 * a*c;
	if (discriminant >= 0) //至少一个交点
	{
		return true;
	}
	else
	{
		return false;
	}
}

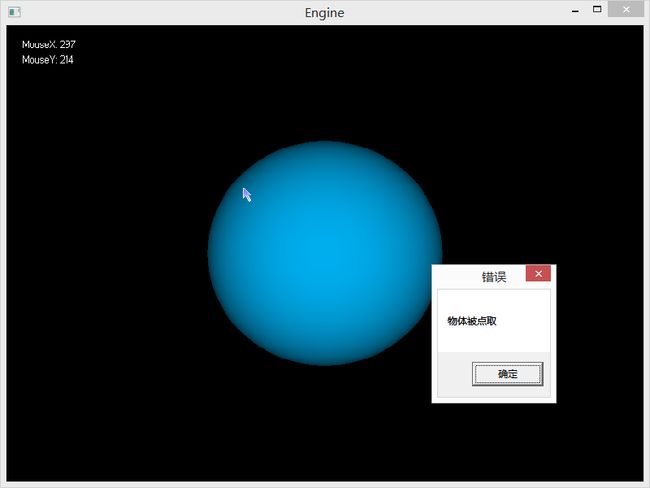
放出程序运行图：

点取(Pick)球体失败：

点取(Pick)球体成功：

最后放出我的源代码链接：

http://download.csdn.net/detail/qq_29523119/9684011