数据结构与算法从零开始系列:冒泡排序、选择排序、插入排序、希尔排序、堆排序、快速排序、归并排序、基数排序
欢迎Star,本文的所有示例源码都在Github:https://github.com/AndroidHensen/Arithmetic
本篇内容包含
- 排序的介绍
- 排序的C的实现
- 排序的Java的实现
- 排序的时间复杂度的计算
(一)冒泡排序
1、基本思想:
两个数比较大小,较大的数下沉,较小的数冒起来
2、实现步骤:
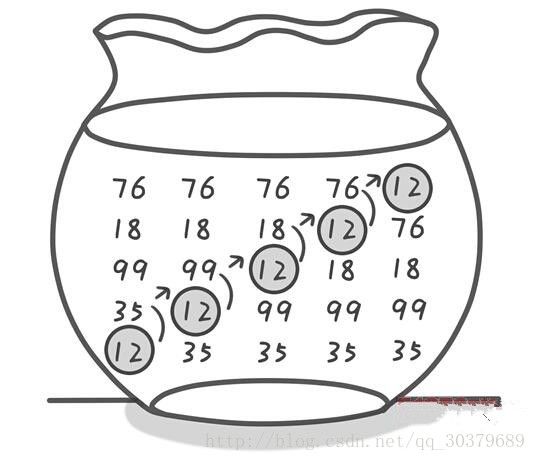
这张图就是将数字12,35,99,18,76竖起来
- 第一次:从底部有一个气泡,圈住12并且和35对比,如果比上面小就交换,气泡往上升
- 第二次:12和99对比,如果比上面小就交换,气泡往上升
- 第三次:重复上面的操作,最后可以把12排到最上面
3、这张图模拟了冒泡排序的整个过程
- 第一个红色框表示气泡
- 两个红色框表示比较大小
- 黑色框表示已经排好的数字
- 最后排成有序的数字
冒泡排序的C的实现
1、程序优化:
- 这里加了一个flag作为优化程序的条件,如果程序未进入内循环,说明数字已经排序好了,后面的比较也就没有意义了,直接程序结束
2、实现口诀:
- 两数相抱转个圈
3、易犯错误:
- 忘记添加优化flag
#include1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
flag =1;
}
}
if(flag == 0)break;
}
}
void main(){
int i;
int arr[10] = {1, 4, 8, 3, 2, 9, 5, 0, 7, 6};
bubbleSort(arr, 10);
//9,8,7,6,5,4,3,2,1,0,
for(i=0; i<10; i++){
printf("%d,", arr[i]);
}
}
冒泡排序的Java的实现
public class BubbleSort {
public void bubbleSort(int[] arr,int n){
boolean flag;
for (int i = 1; i < n; i++) {
flag = false;
for (int j = 0; j < n-i; j++) {
if(arr[j]1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
flag =true;
}
}
if(!flag)break;
}
}
public static void main(String[] args) {
int[] arr = {1, 4, 8, 3, 2, 9, 5, 0, 7, 6};
BubbleSort sort = new BubbleSort();
sort.bubbleSort(arr, arr.length);
//9,8,7,6,5,4,3,2,1,0,
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+",");
}
}
} 冒泡排序的时间复杂度的计算
1、我们从代码分析,可以知道有两个循环
- 外循环:执行(n-1)次,当最坏的情况下,会执行n次,虽然最后一次(i < n)不通过,但还是算一次,其中里面有一条赋值语句
- 内循环:在(i=1,2,3…n-1),执行(n-i)次,即(n-1,n-2…1),其中有四条赋值语句
2、那么就可以计算出各自复杂度
- 外循环:最坏情况下是(1 x n)次
- 内循环:通过等差数列求和公式,(n-1+n-2+…1)=n^2/2
3、根据推导大O阶规则来进行推导
- 用常数1来取代运行时间中所有加法常数
- 修改后的运行次数函数中,只保留最高阶项
- 如果最高阶项存在且不是1,则去除与这个项相乘的常数
4、得到的冒泡排序的复杂度的大O表示法为
(1xn)+(n^2/2) ≈ n^2 = O(n^2)
(二)选择排序
1、基本思想:
- 让第一个数与后面的所有数一个个比较,找出最小的数,将最小的数跟第一个数交换
- 接着从第二个数开始,继续上面的操作
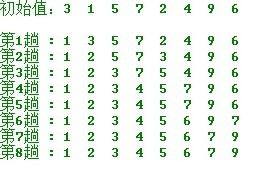
2、实现步骤:
选择排序的C的实现
1、注意点:
- 用语言实现排序的时候,只是记录着最小值的下标,接着用最小值的下标继续和后面的数进行比较,这是和思路不同的地方
2、实现口诀:
- 角标互换
3、易犯错误:
- 忘记添加角标判断
#includeif(minIndex!=i){
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
}
void main(){
int i;
int arr[8] = {3, 1, 5, 7, 2, 4, 9, 6};
selectSort(arr, 8);
//1,2,3,4,5,6,7,9,
for(i=0; i<8; i++){
printf("%d,", arr[i]);
}
}
选择排序的Java的实现
public class SelectSort {
public void selectSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
if (minIndex != i) {
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
}
public static void main(String[] args) {
int[] arr = {3, 1, 5, 7, 2, 4, 9, 6};
SelectSort sort = new SelectSort();
sort.selectSort(arr, arr.length);
//1,2,3,4,5,6,7,9,
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ",");
}
}
}选择排序的时间复杂度的计算
1、我们从代码分析,可以知道有两个循环
- 外循环:执行(n-1)次,当最坏的情况下,会执行n次,虽然最后一次(i < n)不通过,但还是算一次,其中里面有四条赋值语句
- 内循环:在(j=1,2,3…n-1),执行(n-i)次,即(n-1,n-2…1),其中有一条赋值语句
2、那么就可以计算出各自复杂度
- 外循环:最坏情况下是(4 x n)次
- 内循环:通过等差数列求和公式,(n-1+n-2+…1)=n^2/2
3、复杂度的大O表示法为
(4xn)+(1x(n^2/2)) ≈ n^2 = O(n^2)
(三)插入排序
1、基本思想:
- 其实就是你玩扑克牌的时候,排序你自己的牌的思路
- 从后面抽出牌,插入到前面的牌中
2、实现步骤:
- 初始值:1, 4, 8, 3, 2, 9, 5, 0, 7, 6
- 第一次:抽出牌4,与1对比,发现比它大,不交换
- 第二次:抽出牌8,与4对比,发现比它大,不交换
- 第三次:抽出牌3,与8对比,发现比它小,交换,继续与前面一个数比,与4对比,发现比它小,交换,继续与前面一个数比,与1对比,发现比它大,不交换
- 第四次:重复上面步骤,完成扑克牌排序
插入排序的C的实现
1、实现口诀:
- 扑克牌往回插
2、易犯错误:
- 忘记退出的break
#include插入排序的Java的实现
public class InsertSort {
public void insertSort(int[] arr, int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = i + 1; j > 0; j--) {
if (arr[j] < arr[j - 1]) {
int temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
} else {
break;
}
}
}
}
public static void main(String[] args) {
int[] arr = {1, 4, 8, 3, 2, 9, 5, 0, 7, 6};
InsertSort sort = new InsertSort();
sort.insertSort(arr, arr.length);
//0,1,2,3,4,5,6,7,8,9,
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ",");
}
}
}插入排序的时间复杂度的计算
1、我们从代码分析,可以知道有两个循环
- 外循环:执行(n-1)次,当最坏的情况下,会执行n次,虽然最后一次(i < n)不通过,但还是算一次
- 内循环:在(i=0,1,2,3…n-2),执行(n-i-1)次,即(n-1,n-2…1),其中有三条赋值语句
2、那么就可以计算出各自复杂度
- 外循环:最坏情况下是(n)次
- 内循环:通过等差数列求和公式,3x(n-1+n-2+…1)=(3x(n^2/2))
3、复杂度的大O表示法为
(n)+(3x(n^2/2)) ≈ n^2 = O(n^2)
(四)希尔排序
1、基本思想:
- 先对所有的数进行分组
- 对分组的数进行插入排序
2、实现步骤:
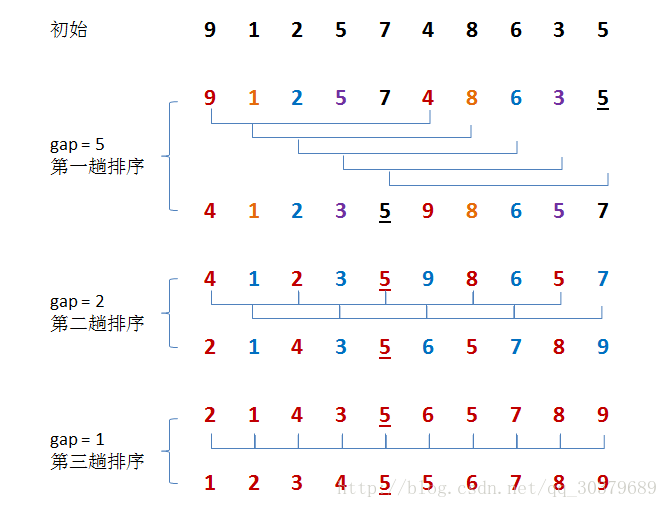
这张图就是将数字9,1,2,5,7,4,8,6,3,5,按分量(数的个数/2)进行分组,然后在各分组中进行插入排序
- 第一次:按分量5分成5组,在组中分别进行插入排序
- 第二次:按分量2分成5组,在组中分别进行插入排序
- 第三次:按分量1分成5组,在组中分别进行插入排序
希尔排序的C的实现
1、实现口诀:
- 分组,插入
2、易犯错误:
- 忘记添加结束break
#includefor (j=i+incre;j<length;j+=incre){
for (k=j;k>i;k-=incre){
if(arr[k]else{
break;
}
}
}
}
if(incre == 1){
break;
}
}
}
int main(){
int i;
int arr[10] = {3, 1, 5, 7, 2, 4, 9, 6, 8, 10};
shellSort(arr,10);
for (i = 0; i < 10; i++) {
printf("%d,",arr[i]);
}
} 希尔排序的Java的实现
public class ShellSort {
public void shellSort(int arr[],int length){
int temp = 0;
int incre = length;
while(true){
incre = incre /2;
//对分组进行遍历
for (int i=0;i//插入排序
for (int j=i+incre;jfor (int k=j;k>i;k-=incre){
if(arr[k]else{
break;
}
}
}
}
//无法分组,表示排序结束
if(incre == 1){
break;
}
}
}
public static void main(String[] args) {
int[] arr = {3, 1, 5, 7, 2, 4, 9, 6, 8, 10};
ShellSort sort = new ShellSort();
sort.shellSort(arr, arr.length);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ",");
}
}
} (五)堆排序
1、基本思想:
- 整理小顶堆
- 将小顶堆a[0]和a[i]和互换
- 将换下来后的a[i]取出,即最大数
- 继续整理小顶堆
堆排序的C的实现
#include
/**
* 整理小顶堆,从i节点开始调整,从0开始计算,i节点的子节点为 2*i+1, 2*i+2
*
* @param a 所有节点
* @param i 第i个节点
* @param n 节点总数
*/
void MinHeapFixdown(int a[], int i, int n) {
int j = 2 * i + 1; //左节点
int temp = 0;
//j
while (j < n) {
//j+1
if (j + 1 < n && a[j + 1] < a[j]) {
//将节点移到右节点
j++;
}
//较大节点在下面
if (a[i] <= a[j])
break;
//较大节点在上面,则将大节点下移
temp = a[i];
a[i] = a[j];
a[j] = temp;
//复位
i = j;
j = 2 * i + 1;
}
}
//构建最小堆
void MakeMinHeap(int a[], int n) {
int i;
//从倒数第二层开始排序,取自己的孩子进行排序,这样所有的节点都排序到了
for (i = (n - 1) / 2; i >= 0; i--) {
MinHeapFixdown(a, i, n);
}
}
void MinHeap_Sort(int a[], int n) {
int i;
int temp = 0;
MakeMinHeap(a, n);
for (i = n - 1; i > 0; i--) {
temp = a[0];
a[0] = a[i];
a[i] = temp;
MinHeapFixdown(a, 0, i);
}
}
int main(){
int i;
int arr[10] = {1, 4, 8, 3, 2, 9, 5, 0, 7, 6};
MinHeap_Sort(arr,10);
for (i = 0; i < 10; i++) {
printf("%d,",arr[i]);
}
} 堆排序的Java的实现
public class HeapSort {
public static void MinHeap_Sort(int a[], int n) {
int temp = 0;
MakeMinHeap(a, n);
for (int i = n - 1; i > 0; i--) {
temp = a[0];
a[0] = a[i];
a[i] = temp;
MinHeapFixdown(a, 0, i);
}
}
//构建最小堆
public static void MakeMinHeap(int a[], int n) {
//从倒数第二层开始排序,取自己的孩子进行排序,这样所有的节点都排序到了
for (int i = (n - 1) / 2; i >= 0; i--) {
MinHeapFixdown(a, i, n);
}
}
/**
* 整理小顶堆,从i节点开始调整,从0开始计算,i节点的子节点为 2*i+1, 2*i+2
*
* @param a 所有节点
* @param i 第i个节点
* @param n 节点总数
*/
public static void MinHeapFixdown(int a[], int i, int n) {
int j = 2 * i + 1; //左节点
int temp = 0;
//j
while (j < n) {
//j+1
if (j + 1 < n && a[j + 1] < a[j]) {
//将节点移到右节点
j++;
}
//较大节点在下面
if (a[i] <= a[j])
break;
//较大节点在上面,则将大节点下移
temp = a[i];
a[i] = a[j];
a[j] = temp;
//复位
i = j;
j = 2 * i + 1;
}
}
public static void main(String[] args) {
int[] arr = {1, 4, 8, 3, 2, 9, 5, 0, 7, 6};
MinHeap_Sort(arr, arr.length);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ",");
}
}
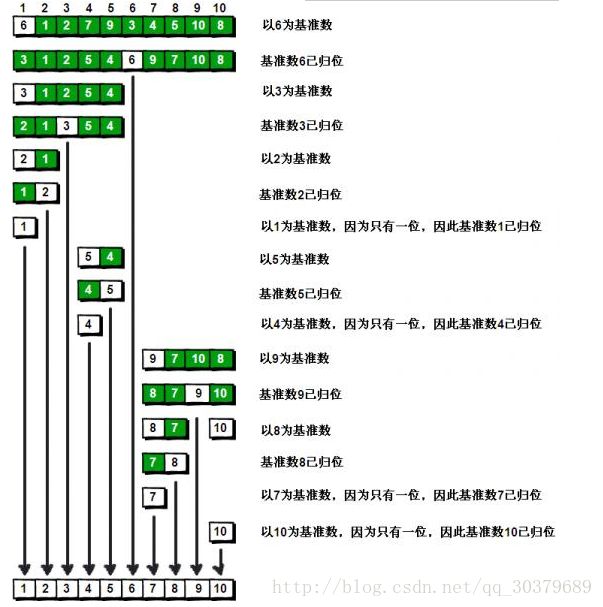
} (六)快速排序
1、基本思想:
- 以第一个数(a)为基准
- 分别在头部和尾部添加指针
- 右边指针先开始,遇到比a小的数则停止
- 左边指针后开始,遇到比a大的数则停止
- 交换右边和左边的指针数
- 重复上述步骤,直到两指针相等
- 交换a与两指针指向的数
快速排序的C的实现
#include
void quicksort(int a[],int left,int right)
{
int i,j,t,temp;
if(left>right)
return;
temp=a[left]; //存基准数
i=left;
j=right;
while(i!=j)
{
//先从右边开始找
while(a[j]>=temp && i//再从左边开始找
while(a[i]<=temp && i//交换两个数在数组中的位置
if(i//基准数归位
a[left]=a[i];
a[i]=temp;
quicksort(a,left,i-1);//继续处理左边的
quicksort(a,i+1,right);//继续处理右边的
}
int main()
{
int arr[10]= {1, 4, 8, 3, 2, 9, 5, 0, 7, 6};
int i;
quicksort(arr,1,10);
for (i = 0; i < 10; i++) {
printf("%d,",arr[i]);
}
return 0;
} 快速排序的Java的实现
public class QuickSort {
public static void quicksort(int a[], int left, int right) {
int i, j, t, temp;
if (left > right)
return;
temp = a[left]; //存基准数
i = left;
j = right;
while (i != j) {
//先从右边开始找
while (a[j] >= temp && i < j)
j--;
//再从左边开始找
while (a[i] <= temp && i < j)
i++;
//交换两个数在数组中的位置
if (i < j) {
t = a[i];
a[i] = a[j];
a[j] = t;
}
}
//基准数归位
a[left] = a[i];
a[i] = temp;
quicksort(a, left, i - 1);//继续处理左边的
quicksort(a, i + 1, right);//继续处理右边的
}
public static void main(String[] args) {
int arr[] = {1, 4, 8, 3, 2, 9, 5, 0, 7, 6};
quicksort(arr, 0, arr.length-1);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ",");
}
}
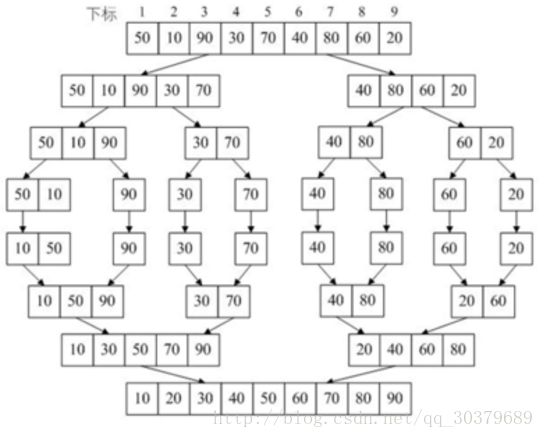
}(七)归并排序
1、基本思想:
- 先将需要排序的数,按中点进行分组
- 重复分组,直到分到的组不能再分
- 比较最后分开的两个组
- 哪个组的数小,就取谁,取了后就在对应数列中删除这个数
- 重复取数,直到两组的数被完全取出,合并取出来的所有数
- 重复上述比较、取数、合并的步骤,最后合并成有序数组
归并排序的Java的实现
public class MergeSort {
/**
* 归并排序
*
* @param a
* @param first
* @param last
* @param temp
*/
public void merge_sort(int a[], int first, int last, int temp[]) {
if (first < last) {
int middle = (first + last) / 2;
merge_sort(a, first, middle, temp);//左半部分排好序
merge_sort(a, middle + 1, last, temp);//右半部分排好序
mergeArray(a, first, middle, last, temp); //合并左右部分
}
}
/**
* 合并数组
*
* @param a
* @param first
* @param middle
* @param end
* @param temp
*/
public void mergeArray(int a[], int first, int middle, int end, int temp[]) {
int i = first;
int m = middle;
int j = middle + 1;
int n = end;
int k = 0;
while (i <= m && j <= n) {
//比较两个组的数
if (a[i] <= a[j]) {
temp[k] = a[i];
k++;
i++;
} else {
temp[k] = a[j];
k++;
j++;
}
}
//左边一组中,当左边分组被取完时,该把右边分组全部取出来
while (i <= m) {
temp[k] = a[i];
k++;
i++;
}
//右边一组中,当左边分组被取完时,该把右边分组全部取出来
while (j <= n) {
temp[k] = a[j];
k++;
j++;
}
//在temp中取出所有排序好的数
for (int ii = 0; ii < k; ii++) {
a[first + ii] = temp[ii];
}
}
public static void main(String[] args) {
int[] arr = {1, 4, 8, 3, 2, 9, 5, 0, 7, 6};
MergeSort sort = new MergeSort();
sort.merge_sort(arr, 0, arr.length - 1, new int[10]);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ",");
}
}
}(八)基数排序
在学习基数排序之前,必须要知道桶排序,所以先简单的学习一下桶排序
1、基本思想:
- 首先创建数组A[MaxValue]
- 将每个数放到相应的位置上,即数的值和索引相等的位置
- 最后遍历数组,即为排序后的结果
桶排序的Java的实现
public class BucketSort {
public void sort(int[] keys, int bucketNum) {
int len = keys.length;
int[] bucket = new int[bucketNum];
//初始化每个桶
for (int i = 0; i < bucketNum; i++) {
bucket[i] = 0;
}
//为每个数添加到对应桶
for (int i = 0; i < len; i++) {
bucket[keys[i]]++;
}
//遍历数组,即为结果
for (int i = 0; i < bucketNum; i++) {
for (int j = 1; j <= bucket[i]; j++) {
System.out.print(i + ",");
}
}
}
public static void main(String[] args) {
int[] a = {1, 4, 8, 3, 2, 9, 5, 0, 7, 6, 9, 10, 9, 13, 14, 15, 11, 12, 17, 16, 19};
BucketSort sorter = new BucketSort();
sorter.sort(a, 20);
}
}基数排序
1、基本思想:
- 将每个数的个位开始进行桶排序
- 排序完成后,桶按顺序输出
- 将排序好个位的数,进行十位开始桶排序
- 排序完成后,桶按顺序输出
- 重复上述步骤,直到最高位进行桶排序,按顺序输出即为结果
基数排序的Java的实现
public class RadixSort {
/**
* @param arr 原数组
* @param temp 临时数组
* @param n 序列的数字个数
* @param k 最大的位数3
* @param r 基数10
* @param bin 桶中i位置存储的个数
*/
public void radixSort(int arr[], int temp[], int n, int k, int r, int bin[]) {
//digit:位数,个位、十位、百位等
for (int i = 0, digit = 1; i < k; i++, digit = digit * r) {
//初始化
for (int j = 0; j < r; j++) {
bin[j] = 0;
}
//计算每个箱子的数字个数
for (int j = 0; j < n; j++) {
bin[(arr[j] / digit) % r]++;
}
//bin[j]的个数修改为前j个箱子一共有几个数字
for (int j = 1; j < r; j++) {
bin[j] = bin[j - 1] + bin[j];
}
//取出每个
for (int j = n - 1; j >= 0; j--) { //重点理解
bin[(arr[j] / digit) % r]--;
temp[bin[(arr[j] / digit) % r]] = arr[j];
}
//将临时数组赋值给我们的数组
for (int j = 0; j < n; j++) {
arr[j] = temp[j];
}
}
}
public static void main(String[] args) {
int[] arr = {143, 454, 812, 343, 245, 913, 565, 12, 743, 632};
RadixSort sort = new RadixSort();
sort.radixSort(arr, new int[10], arr.length, 3, 10, new int[10]);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ",");
}
}
}总结
| 排序类型 | 时间复杂度 |
|---|---|
| 冒泡排序 | O(n^2) |
| 选择排序 | O(n^2) |
| 插入排序 | O(n^2) |
| 希尔排序 | O(n^1.5) |
| 堆排序 | O(N*logN) |
| 快速排序 | O(N*logN) |
| 归并排序 | O(N*logN) |
| 基数排序 | O(d(n+r)) |