图像处理基本算法之空间域图像增强
图像增强技术根据增强处理过程所在的空间不同,可分为基于频域的算法和基于空域的算法两大类。基于频域的算法是在图像的某种变换域内对图像的变换系数值进行某种修正,是一种间接增强的算法,把图像看成一种二维信号,对其进行基于二维傅里叶变换的信号增强。采用低通滤波(即只让低频信号通过)法,可去掉图中的噪声;采用高通滤波法,则可增强边缘等高频信号,使模糊的图片变得清晰。基于空域的算法处理时直接对图像灰度级做运算,空间域法中具有代表性的算法有局部求平均值法和中值滤波(取局部邻域中的中间像素值)法等,它们可用于去除或减弱噪声。
图像增强的方法是通过一定手段,有选择地突出图像中感兴趣的特征或者抑制(掩盖)图像中某些不需要的特征。在图像增强过程中,不分析图像降质的原因,处理后的图像不一定逼近原始图像。
基于空域的算法分为点运算算法和邻域去噪算法。点运算算法即灰度级校正、灰度变换和直方图修正等,目的或使图像成像均匀,或扩大图像动态范围,扩展对比度。邻域增强算法分为图像平滑和锐化两种。平滑一般用于消除图像噪声,但是也容易引起边缘的模糊。常用算法有均值滤波、中值滤波。锐化的目的在于突出物体的边缘轮廓,便于目标识别。常用算法有梯度法、算子、高通滤波、掩模匹配法、统计差值法等。
图像增强处理以下情况:
(1)图像太暗;
(2)图像太亮;
(3)有噪声点;
(4)对比度不明显。
空间域图像增强的方法:
1)针对每一个像素处理
① 简单变换(取反,线性变换,指数变换,对数变换,幂次变换);
② 使用滤波器(算子)。参见:图像常用滤波方法(方框、均值、高斯、中值、双边)
2)针对一组像素处理(直方图)
① 直方图均衡
② 直方图匹配
2.常用函数:
⑴ 取反(底片效果):imcomplement()
⑵ 二值化:~im2bw
⑶ 线性变换
⑷ 指数变换: exp()
⑸ 对数变换: log()
⑹ 幂次变换: power()
⑺ 查看直方图: imhist()
⑻ 使用直方图均衡:Histeq()
⑼ 使用平滑滤波器:(imfilter实现函数滤波)
⑽ 使用锐化滤波器
⑾ 旋转、缩放、剪切等: imrotate imresize imcrop
⑿ 对比度增强:imadjust()
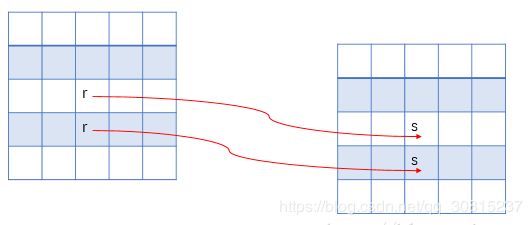
图像反转:
就是把黑变白,白变黑,图像反转适用于增强嵌入于图像暗色区域的白色或灰色细节,物别是当黑色面积占主导地位时。
表达式:![]()
r:原图像;s是变换后的图像
对数变换:
此变换使一窄带低灰度输入图像值映射为一宽带输出值。相对的是输入灰度的高调整值。可以利用这种变换来扩展被压缩的高值图像中的暗像素。相对的是反对数变换的调整值。
图像的对数变换作用:
由于对数曲线在像素值较低的区域斜率大,在像素值较高的区域斜率较小,所以图像经过对数变换后,较暗区域的对比度将有所提升,所以就可以增强图像的暗部细节。
表达式:![]()
底数v越大,对低灰度部分的强调就越强,对高灰度部分的压缩也就越强。相反的,如果想强调高灰度部分,则用反对数函数就可以了。看下面的实验就可以很直观的理解,下图是某图像的二维傅里叶变换图像,其为了使其灰度部分较为明显,一般都会使用灰度变换处理一下。
幂次变换:
又叫伽玛校正,幂次变换的基本表达式为:
![]()
其中c、r均为正数。与对数变换相同,幂次变换将部分灰度区域映射到更宽的区域中。当r=1时,幂次变换转变为线性变换。
(1) 当0<r<1时,变换函数曲线在正比函数上方。此时扩展低灰度级,压缩高灰度级,使图像变亮。与对数变换十分相似。
(2) 当r>1时,变换函数曲线在正比函数下方。此时扩展高灰度级,压缩低灰度级,使图像变暗。
一个拉伸高像素值的范围,一个拉伸低像素值的范围。哪部分的斜率越大,哪部分的拉伸比例就越大。
这里选择的参数为c = 1,γ=3,来扩展图像的高灰度区域,其结果如下:
当选择参数为c = 1,γ=0.4,来扩展图像的低灰度区域,其效果如下:
- γ>1时,会将低于某个灰度值K的灰度区域压缩到较小的灰度区间,而将高于K的灰度区域扩展到较大灰度区间。令L为灰度的最大值,k = 3/4L . 那么就有[0,3/4L][0,3/4L]的灰度区域映射到为[0,1/8L][0,1/8L]的输出;而将[3/4L,L][3/4L,L]这部分高灰度区域映射到[1/8L,L][1/8L,L]区间。这样变换的结果就是,低于K的灰度区域被压缩到更低灰度区间,而较亮的高灰度区域的灰度值被扩展到较大的灰度区间变的不那么亮,整体的效果就是图像的对比度增加了,但是由于亮度区域被扩展,也就不那么亮了。
- γ<1时,会将灰度值较小的低灰度区域扩展到较宽的灰度区间,而将较宽的高灰度区域压缩到较小的灰度区间。这样变换的效果就是,低灰度区域扩展开来,变亮;而宽的高灰度区域,被压缩的较窄的区间,也变亮了,故变换后的整体效果是变亮了。
指数变换
指数变换的基本表达式为:![]()
其中参数b、c控制曲线形状,参数a控制曲线的左右位置。
从数学角度来想,指数随着横坐标变大曲线变得越来越陡峭,指数变换拉大了不同点的灰度值距离,所以指数变换提高了图像的对比度,当然它主要目的是进一步提高灰度值高的像素点。
指数变换的作用是扩展图像的高灰度级、压缩低灰度级。虽然幂次变换也有这个功能,但是图像经过指数变换后对比度更高,高灰度级也被扩展到了更宽的范围。
灰度拉伸
灰度拉伸也用于强调图像的某个部分,与伽马变换与对数变换不同的是,灰度拉升可以改善图像的动态范围。可以将原来低对比度的图像拉伸为高对比度图像。实现灰度拉升的方法很多,其中最简单的一种就是线性拉伸。
这里介绍稍微复杂一些的方法。灰度拉伸所用数学式如下所示。
![]()
注意:输入为0时候,式子无意义了。所以,在计算的时候,将其变为如下形式。
![]()
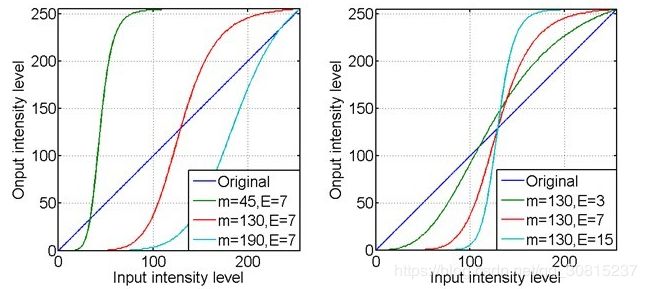
灰度拉伸的输入输出曲线如下图所示。
有两个参数,一个是m(相对于巴特沃斯高通滤波器而言,这个是截止频率),一个是E(相对于巴特沃斯高通滤波器而言,这个是滤波器次数)。m可以控制变换曲线的重心,E则可以控制曲线的斜率,如下图所示。
m值的可取图像灰度分布的中央值

灰度拉升的目的就是扩展图片的动态范围,我们想将原本灰度范围是![]() 的图像变换到【0,1】内。那么,就直接取最大值与最小值,带入式子,解出E就可以了。但是,如之前所说的,我们所用的式子的的输出范围达不到
的图像变换到【0,1】内。那么,就直接取最大值与最小值,带入式子,解出E就可以了。但是,如之前所说的,我们所用的式子的的输出范围达不到![]() ,而且,直接取
,而且,直接取![]() 的范围,会造成E非常大,从而变换曲线的斜率非常大,灰度扩展的结果并不是很好。所以,这里退一步,取的输出范围是
的范围,会造成E非常大,从而变换曲线的斜率非常大,灰度扩展的结果并不是很好。所以,这里退一步,取的输出范围是![]() 。E的取值,如下所示。
。E的取值,如下所示。
位图切割
位图切割,就是按照图像的位,将图像分层处理。若图像的某个像素,其bit7为1,则在位面7这个像素值为1,反之则为0。由位图切割的结果可以看出,图像的主要信息包含在了高4位。仅仅靠高4位,还原的图像更原图基本差不多。由此可见,位图切割主要用于图像压缩
直方图均衡化
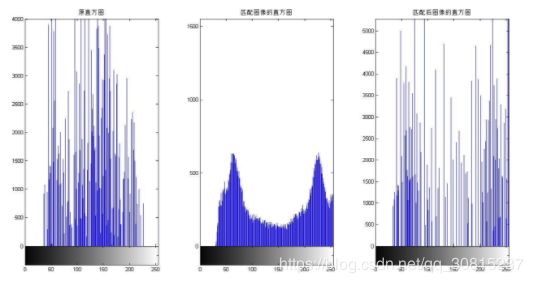
直方图均衡化(Histogram Equalization) 又称直方图平坦化,实质上是对图像进行非线性拉伸,重新分配图像象元值,使一定灰度范围内象元值的数量大致相等。这样,原来直方图中间的峰顶部分对比度得到增强,而两侧的谷底部分对比度降低,输出图像的直方图是一个较平的分段直方图:如果输出数据分段值较小的话,会产生粗略分类的视觉效果。
直方图是表示数字图像中每一灰度出现频率的统计关系。直方图能给出图像灰度范围、每个灰度的频度和灰度的分布、整幅图像的平均明暗和对比度等概貌性描述。灰度直方图是灰度级的函数, 反映的是图像中具有该灰度级像素的个数, 整个坐标系描述的是图像灰度级的分布情况, 由此可以看出图像的灰度分布特性, 即若大部分像素集中在低灰度区域, 图像呈现暗的特性; 若像素集中在高灰度区域, 图像呈现亮的特性。
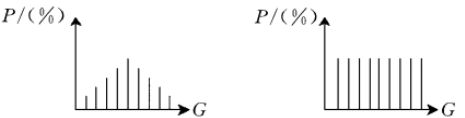
下图就是直方图均衡化, 即将随机分布的图像直方图修改成均匀分布的直方图。基本思想是对原始图像的像素灰度做某种映射变换, 使变换后图像灰度的概率密度呈均匀分布。这就意味着图像灰度的动态范围得到了增加, 提高了图像的对比度。
直方图均衡化的作用是图像增强。这种方法对于背景和前景都太亮或者太暗的图像非常有用,采用选用累积分布函数对灰度值进行映射。对其进行直方图均衡化步骤如下:
1、 统计直方图,
2、 求出对应的概率密度
3、求累积分布函数
4、求出每个灰度级对应的输出灰度级
5、映射到新的图像
为什么要选用累积分布函数,使用累积分布函数处理后像素值会均匀分布?
均衡化过程中,必须要保证两个条件:
①像素无论怎么映射,一定要保证原来的大小关系不变,亮暗关系不变,只是对比度增大,绝对不能明暗颠倒;
②如果是八位图像,那么像素映射函数的值域应在0和255之间的,不能越界。
综合以上两个条件,累积分布函数是个好的选择,因为累积分布函数是单调增函数(控制大小关系),并且值域是0到1(控制越界问题),所以直方图均衡化中使用的是累积分布函数。
此外,累积分布函数具有一些好的性质,比较概率分布函数和累积分布函数,前者的二维图像是参差不齐的,后者是单调递增的。直方图均衡化过程中,映射方法是
其中,n是图像中像素的总和,n_k是当前灰度级的像素个数,L是图像中可能的灰度级总数。
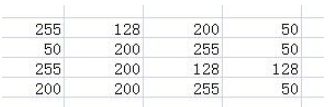
来看看通过上述公式怎样实现的拉伸。假设有如下图像:
得图像的统计信息如下图所示,并根据统计信息完成灰度值映射:
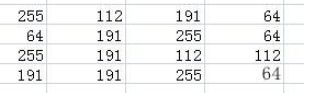
映射后的图像如下所示:
![]()
根据上表:0→1;1→2;2→2;3→3;4→3;5→4;6→4;7→7;
from:https://wenku.baidu.com/view/691609fe690203d8ce2f0066f5335a8103d26639.html
直方图匹配
与直方图均衡不同的一点是,直方图匹配要得到的是具有特定形状的直方图的图像。当图像中接近0的像素过多,进行直方图均衡的时候,会导致统计概率变大,直接映射到高灰度,直接导致图像整体变量,达不到原来想要的结果,此时就需要使用直方图匹配,让变化后的图像具有特定的直方图。有时候,我们为了使两幅图像的色调保持一致,也可以采用该方法。
直方图匹配的计算过程:
1. 计算输入图像的每个灰度级的累积分布函数 T(r)
2. 计算模板直方图的每个灰度级的累积分布函数G(z)。
3. 令G(z) = T(r),求出r→z,当不止一个z满足时,通常选择最小的值。
r→z的求解:r→z表示对于一个r(对于L = 256的灰度直方图,r取0,1,2,...,254,255),找出满足T(r) = G(z)的z,若不存在,则找出最接近的z(即找出min(abs( T(r) - G(z) ) 对应的z)。当z有多个时,通常取最小的。
4、最后和直方图均衡化的最后一步一样,逐个像素进行映射
运行结果:
from:学习笔记(二)——直方图均衡化和匹配
from:直方图均衡化
from:空间域图像增强
from:https://blog.csdn.net/u012856866/article/details/22064751