数据结构之图--最小生成树（普里姆（Prim）算法）

（在通信网络上用的多）

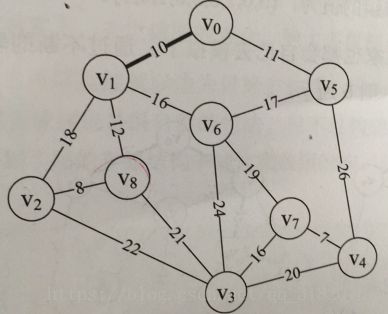
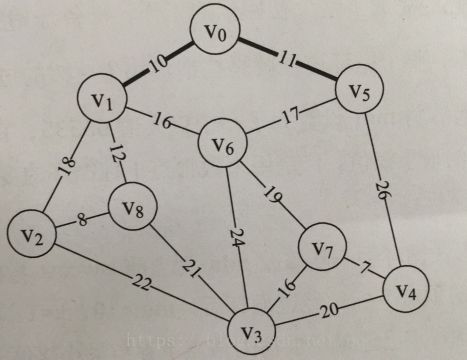
构造连通网的最小代价生成树称为最小生成树。（找到最小代价连接所有结点）（n个顶点则要找n-1条边出来）

两种构建最小生成树的方法：普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法

一、普里姆（Prim）算法（时间复杂度n²）（加点法）

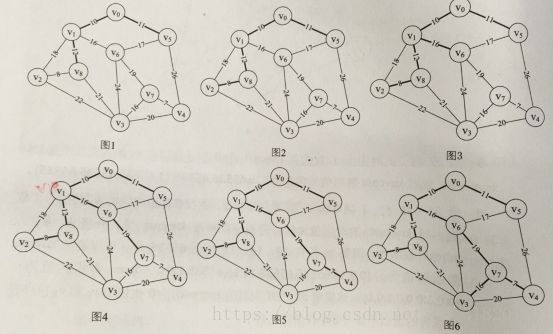
    思想：每次迭代寻找与已加入生成树的点所组成最小边长的非生成树中的点，将此点加入树中，由此循环。

        根据思想需要定义两个一维数组：树中顶点下标adjvex[MAXVEX]，（例如：adjvex[2]=8，adjvex[8]=4表示点4连着点8，点8连着点2）；边长矩阵lowcost[MAXVEX]，lowcost[j]=0表示点j加入了生成树，每次迭代在lowcost[i]中选出非0的最小值保存下标i，lowcost[i]存着非生成树中点i连接生成树中点的最小边长；用if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) 来改变非生成树中点j连接生成树中点的最小边长和j所连接生成树中点k（即adjvex[j]=k）。

·

上图在执行代码过程中lowcost变化过程：{0,10,65535,65535,65535,11,65535,65535,65535}（初始化）-->{0,0,65535,65535,65535,11,65535,65535,65535}-->{0,0,18,65535,65535,11,16,65535,12}

adjvex变化过程：{0,0,0,0,0,0,0,0,0}（初始化）-->{0,0,1,0,0,0,1,0,1}

代码实现：

#include "stdio.h"    
#include "stdlib.h"   
#include "io.h"  
#include "math.h"  
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXEDGE 20
#define MAXVEX 20
#define INFINITY 65535

typedef int Status;	/* Status是函数的类型,其值是函数结果状态代码，如OK等 */

typedef struct
{
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}MGraph;

void CreateMGraph(MGraph *G)/* 构件图 */
{
	int i, j;

	/* printf("请输入边数和顶点数:"); */
	G->numEdges=15;
	G->numVertexes=9;

	for (i = 0; i < G->numVertexes; i++)/* 初始化图 */
	{
		for ( j = 0; j < G->numVertexes; j++)
		{
			if (i==j)
				G->arc[i][j]=0;
			else
				G->arc[i][j] = G->arc[j][i] = INFINITY;
		}
	}

	G->arc[0][1]=10;
	G->arc[0][5]=11; 
	G->arc[1][2]=18; 
	G->arc[1][8]=12; 
	G->arc[1][6]=16; 
	G->arc[2][8]=8; 
	G->arc[2][3]=22; 
	G->arc[3][8]=21; 
	G->arc[3][6]=24; 
	G->arc[3][7]=16;
	G->arc[3][4]=20;
	G->arc[4][7]=7; 
	G->arc[4][5]=26; 
	G->arc[5][6]=17; 
	G->arc[6][7]=19; 

	for(i = 0; i < G->numVertexes; i++)
	{
		for(j = i; j < G->numVertexes; j++)
		{
			G->arc[j][i] =G->arc[i][j];
		}
	}

}

/* Prim算法生成最小生成树  */
void MiniSpanTree_Prim(MGraph G)
{
	int min, i, j, k;
	int adjvex[MAXVEX];		/* 保存相关顶点下标 */
	int lowcost[MAXVEX];	/* 保存相关顶点间边的权值 */
	lowcost[0] = 0;/* 初始化第一个权值为0，即v0加入生成树 */
			/* lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */
	adjvex[0] = 0;			/* 初始化第一个顶点下标为0 */
	for(i = 1; i < G.numVertexes; i++)	/* 循环除下标为0外的全部顶点 */
	{
		lowcost[i] = G.arc[0][i];	/* 将v0顶点与之有边的权值存入数组 */
		adjvex[i] = 0;					/* 初始化都为v0的下标 */
	}
	for(i = 1; i < G.numVertexes; i++)
	{
		min = INFINITY;	/* 初始化最小权值为∞， */
						/* 通常设置为不可能的大数字如32767、65535等 */
		j = 1;k = 0;
		while(j < G.numVertexes)	/* 循环全部顶点 */
		{
			if(lowcost[j]!=0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */
			{	
				min = lowcost[j];	/* 则让当前权值成为最小值 */
				k = j;			/* 将当前最小值的下标存入k */
			}
			j++;
		}
		printf("(%d, %d)\n", adjvex[k], k);/* 打印当前顶点边中权值最小的边 */
		lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */
		for(j = 1; j < G.numVertexes; j++)	/* 循环所有顶点 */
		{
			if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) 
			{/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */
				lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */
				adjvex[j] = k;				/* 将下标为k的顶点存入adjvex */
			}
		}
	}
}

int main(void)
{
	MGraph G;
	CreateMGraph(&G);
	MiniSpanTree_Prim(G);
  
	return 0;
 
}