分治法习题整理
分治法
1.POJ3714
题目:
The system was charged by N nuclear power stations and breaking down any of them would disable the system.
The general soon started a raid to the stations by N special agents who were paradroped into the stronghold. Unfortunately they failed to land at the expected positions due to the attack by the Empire Air Force. As an experienced general, Arthur soon realized that he needed to rearrange the plan. The first thing he wants to know now is that which agent is the nearest to any power station. Could you, the chief officer, help the general to calculate the minimum distance between an agent and a station?
The first line is a integer T representing the number of test cases.
Each test case begins with an integer N (1 ≤ N ≤ 100000).
The next N lines describe the positions of the stations. Each line consists of two integers X (0 ≤ X ≤ 1000000000) and Y (0 ≤ Y ≤ 1000000000) indicating the positions of the station.
The next following N lines describe the positions of the agents. Each line consists of two integers X (0 ≤ X ≤ 1000000000) and Y (0 ≤ Y ≤ 1000000000) indicating the positions of the agent.
最近点对问题,注意是station与agent类间的最近点对。
算法描述:
需要定义⼀个Pointer的结构来存储station和agent的坐标(即x值与y值),还包含⼀个flag用来标记坐标是属于station还是agent。
- 先将输⼊的坐标数据按x排序,然后二分求解。
- 在合并子问题时,只需考虑横跨左右的答案。
- 取出所有与分界点x坐标之差不不超过左右子问题最⼩值ans的点,只有这些才是可能解。
- 将这些点按y排序。
- 对于每个点,只与和它y坐标之差不超过ans的点计算距离,直到找到最短的距离。
代码:
#include
#include
#include
#include
#include
using namespace std;
const int N = 200000 + 1;
const double INF = 1e100;
struct Pointer{
double x,y;
bool flag;
};
Pointer m[N + 1];
int tmp[N + 1];
double dis(Pointer a,Pointer b){
return sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
}
bool cmpx(Pointer a,Pointer b){
return a.x < b.x;
}
bool cmpy(int a,int b){
return m[a].y < m[b].y;
}
double getMinLen(Pointer *s,int left,int right){
double rs = INF;
if (left == right)
return rs;
if (left + 1 == right) {
if (s[left].flag == s[right].flag)
return rs;
return dis(s[left], s[right]);
}
int mid = (left + right) / 2;
rs = getMinLen(s, left, mid);
double temp = getMinLen(s, mid + 1, right);
rs = rs <= temp ? rs:temp;
//开始实际计算
int i,j,num = 0;
for (i = left; i <= right; i++)
if (fabs(s[i].x - s[mid].x) <
= rs)
tmp[num++] = i;
sort(tmp, tmp + num, cmpy);
double d = INF;
for (i = 0; i < num; i++) {
for (j = i + 1; j < num; j++) {
if (fabs(s[tmp[i]].y - s[tmp[j]].y) >= rs)
break;
if (s[tmp[i]].flag != s[tmp[j]].flag && (d = dis(s[tmp[i]], s[tmp[j]])) < rs)
rs = d;
}
}
return rs;
}
int main(){
int t,n;
cin >> t;
while (t--) {
cin >> n;
//输入station的坐标,flag置为false
for (int i = 0; i < n; i++) {
cin >> m[i].x >> m[i].y;
m[i].flag = false;
}
//输入agent的坐标,flag置为true
for (int j = 0; j < n; j++) {
cin >> m[j + n].x >> m[j + n].y;
m[j + n].flag = true;
}
n *= 2;
//先按照x坐标排序
sort(m, m + n, cmpx);
double ans = getMinLen(m,0,n);
cout << fixed << setprecision(3) << ans << endl;
}
return 0;
}
2.中位数
题目:
算法思路:
较为直观,但代码有很多细节问题
代码:
#include
using namespace std;
const int N = 100000;
int A[N],B[N];
double findMid(int l1,int r1,int l2,int r2){
int pos1 = (l1 + r1) / 2;
int pos2 = (l2 + r2) / 2;
double mid1,mid2;
if (r1 == l1)
return (A[l1] + B[l2]) / 2.0;
if ((r1 - l1 + 1) % 2 == 0)
mid1 = (A[pos1] + A[pos1 + 1]) / 2.0;
else
mid1 = A[pos1];
if ((r2 - l2 + 1) % 2 == 0)
mid2 = (B[pos2] + B[pos2 + 1]) / 2.0;
else
mid2 = B[pos2];
if (mid1 < mid2){
pos1 = (r1 - l1) % 2 ? (pos1 + 1) : pos1;
return findMid(pos1, r1, l2, pos2);
}
else
if(mid1 > mid2){
pos2 = (r2 - l2) % 2 ? (pos2 + 1) : pos2;
return findMid(l1, pos1, pos2, r2);
}
else
return mid1;
}
int main(){
int n;
cout << "Please input n:";
cin >> n;
for (int i = 0;i < n;i++)
cin >> A[i];
for (int i = 0;i < n;i++)
cin >> B[i];
double ans = findMid(0,n-1,0,n-1);
cout << ans << endl;
return 0;
}
3.逆序对
题目:
算法思路:
本质上就是做归并排序,只不过在其中增加一个小步骤统计逆序对的数量
代码:
#include
#include
using namespace std;
int reversePair(int arr[], int temp[], int left, int right);
int merge(int arr[], int temp[], int left, int mid, int right);
int main(void) {
int test[100];
int t[100];//临时数组用于合并步骤,不在递归函数中开启数组,防止递归过程内存中同时存在大量数组
int n;
cout << "请输入n:";
cin >> n;
for (int i = 0;i < n;i++)
cin >> test[i];
cout << reversePair(test, t, 0, n - 1) << endl;
return 0;
}
int reversePair(int arr[], int temp[], int l, int r) {
if(l == r)
return 0;
int m = (l + r) / 2;
int ln = reversePair(arr, temp, l, m);//左序列逆序对数量
int rn = reversePair(arr, temp, m + 1, r);//右序列逆序对数量
int mn = merge(arr, temp, l, m, r);//左序列与右序列元素构成的逆序对数量
return ln + rn + mn;
}
int merge(int arr[], int temp[], int l, int m, int r) {
int count = 0, i, j;
for(i = l; i <= r; i++)
temp[i] = arr[i];
int k = l;
for(i = l, j = m + 1; i <= m && j <= r;k++) {
if(temp[i] > temp[j]) {
count += m - i + 1;//每次发现左序列元素比右序列元素大,逆序对数量增加,m-i+1即为该元素到左序列尾的元素数量
//其余代码为归并排序的步骤
//arr数组为排好序的新数组
arr[k] = temp[j];
j++;
}
else {
arr[k] = temp[i];
i++;
}
}
if(i > m) {
//i到底了,j还没到
while(j <= r) {
arr[k] = temp[j];
j++;
k++;
}
}
else {
//j到底了,i还没到
while(i <= m) {
arr[k] = temp[i];
i++;
k++;
}
}
return count;
}
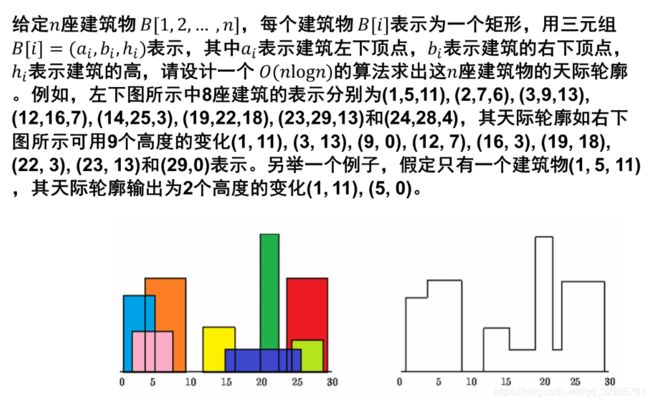
4.天际线
题目:
算法思路:
首先怎么分:
不停对半分
停止条件1:为空时,直接返回空
停止条件2:大小为1时,直接返回左上角点和右下角点。
那么怎么合并?
维护两个变量:l,r l为左半部分当前位置,r为右半部分当前位置
维护两个变量:h1,h2 h1表示左半部分当前位置高度,h2表示右半部分当前位置高度
如果当前位置左半部分横坐标更小,就更新h1,从左半部分选元素;
如果当前位置右半部分横坐标更小,就更新h2,从右半部分选元素;
如果一样大,就更新h1,h2,从左(或右)半部分选元素
当向结果中插入点时,只有和结果中最后一个点高度不同的点才能插入到结果里,且一直使用高度max(h1,h2)。
当某一部分全部访问过后,就将另一部分(和结果中最后一个点高度不同的点)直接插入结果里。
代码:
//
// 天际线.cpp
// ACM
//
// Created by 游文彦 on 2018/10/4.
// Copyright © 2018 Swallow. All rights reserved.
//
#include
using namespace std;
struct Building{
int left;
int right;
int height;
};
class Strip{
int left;
int height;
public:
Strip(int l = 0,int h = 0){
left = l;
height = h;
}
friend class SkyLine;
};
class SkyLine{
Strip * arr;
int capacity;
int n;
public:
~SkyLine(){
delete [] arr;
}
int count(){
return n;
}
SkyLine * Merge(SkyLine * other);
SkyLine(int cap){
capacity = cap;
arr = new Strip[cap];
n = 0;
}
void append(Strip *sp){
//如果新加入的节点高度与之前节点一样,则不加入进去
if (n > 0 && arr[n - 1].height == sp->height)
return;
//如果新加入的节点left坐标与之前节点一样,则取其高度高的作为height
if (n > 0 && arr[n - 1].left == sp->left) {
arr[n].height = max(arr[n - 1].height,sp->height);
return;
}
arr[n] = *sp;
n++;
}
void print(){
for (int i = 0; i < n; i++)
cout << "(" << arr[i].left << "," << arr[i].height << ")" << ",";
cout << endl;
}
};
SkyLine * findSkyLine(Building arr[],int l,int r){
if (l == r) {
SkyLine * ans = new SkyLine(2);
//左上
ans->append(new Strip(arr[l].left,arr[l].height));
//右下
ans->append(new Strip(arr[l].right,0));
return ans;
}
int mid = (l + r) / 2;
SkyLine *sl = findSkyLine(arr, l, mid);
SkyLine *sr = findSkyLine(arr, mid + 1, r);
SkyLine *ans = sl->Merge(sr);
delete sl;
delete sr;
return ans;
}
SkyLine *SkyLine::Merge(SkyLine * other){
SkyLine * ans = new SkyLine(this->n + other->n);
int h1 = 0,h2 = 0;
int i = 0,j = 0;
while (i < this->n && j < other->n) {
if (this->arr[i].left < other->arr[j].left) {
int x1 = this->arr[i].left;
h1 = this->arr[i].height;
int maxh = max(h1,h2);
ans->append(new Strip(x1,maxh));
i++;
}
else{
int x2 = other->arr[j].left;
h2 = other->arr[j].height;
int maxh = max(h1,h2);
ans->append(new Strip(x2,maxh));
j++;
}
}
//如果左边还没到底
while (i < this->n) {
ans->append(&this->arr[i]);
i++;
}
//如果右边还没到底
while (j < other->n) {
ans->append(&other->arr[j]);
j++;
}
return ans;
}
int main(){
// Building arr1[] ={{1, 5, 11}, {2, 7, 6}, {3, 9, 13},
// {12, 16, 7}, {14, 25, 3}, {19, 22, 18},
// {23, 29, 13}, {24, 28, 4}};
Building arr1[] = {{1,4,3},{2,6,5},{3,7,4},{9,10,7}};
int n = sizeof(arr1) / sizeof(arr1[0]);
SkyLine *ptr = findSkyLine(arr1, 0, n - 1);
ptr->print();
return 0;
}