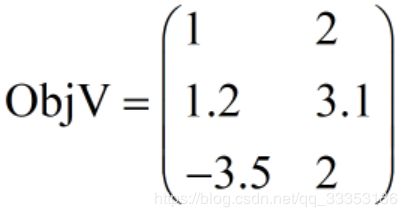Python遗传和进化算法框架(一)Geatpy快速入门
Geatpy是一个高性能实用型的Python遗传算法工具箱,提供一个面向对象的进化算法框架,经过全面改版后,新版Geatpy2目前由华南农业大学、暨南大学、华南理工等本硕博学生联合团队开发及维护。
- Website (including documentation): http://www.geatpy.com
- Demo : https://github.com/geatpy-dev/geatpy/tree/master/geatpy/demo
- Pypi page : https://pypi.org/project/geatpy/
- Contact us: http://geatpy.com/index.php/about/
- Bug reports: https://github.com/geatpy-dev/geatpy/issues
- Notice: http://geatpy.com/index.php/notice/
- FAQ: http://geatpy.com/index.php/faq/
Geatpy提供了许多已实现的遗传和进化算法相关算子的库函数,如初始化种群、选择、交叉、变异、重插入、多目标优化非支配排序等,并且提供诸多已实现的进化算法模板来实现多样化的进化算法。其执行效率高于Matlab、Java和Python编写的一些知名工具箱、平台或框架等,学习成本低、模块高度脱耦、扩展性高。
Geatpy支持二进制/格雷码编码种群、实数值种群、整数值种群、排列编码种群。支持轮盘赌选择、随机抽样选择、锦标赛选择。提供单点交叉、两点交叉、洗牌交叉、部分匹配交叉(PMX)、顺序交叉(OX)、线性重组、离散重组、中间重组等重组算子。提供简单离散变异、实数值变异、整数值变异、互换变异等变异算子。支持随机重插入、精英重插入。支持awGA、rwGA、nsga2、快速非支配排序等多目标优化的库函数、提供进化算法框架下的常用进化算法模板等。
关于遗传算法、进化算法的学习资料,在官网中https://www.geatpy.com 有详细讲解以及相关的学术论文链接。同时网上也有很多资料。
闲话少说……下面讲一下怎么安装和使用:
先说一下安装方法:
首先是要windows系统,Python要是3.5,3.6或3.7版本 ,并且安装了pip。只需在控制台执行
pip install geatpy即可安装成功。或者到github上下载源码进行编译安装:https://github.com/geatpy-dev/geatpy 。推荐是直接用pip的方式安装。因为这样方便后续的更新。我为了方便运行demo代码以及查看源码和官方教程文档,因此另外在github上也下载了(但仍用pip方式安装)。
有些初学Python的读者反映还是不知道怎么安装,或者安装之后不知道怎么写代码。这里推荐安装Anaconda,它集成了Python的许多常用的运行库,比如Numpy、Scipy等。其内置的Spyder开发软件的风格跟Matlab类似,给人熟悉的感觉,更容易上手。
再说一下更新方法:
Geatpy在持续更新。可以通过以下命令使电脑上的版本与官方最新版保持一致:
pip install --upgrade geatpy若在更新过程中遇到"--user"错误的问题,这是用pip进行安装时遇到的常见问题之一。意味着需要以管理员方式运行:
pip install --user --upgrade geatpyGeatpy提供2种方式来使用进化算法求解问题。先来讲一下第一种最基本的实现方式:编写编程脚本。
1. 编写脚本实现遗传算法:
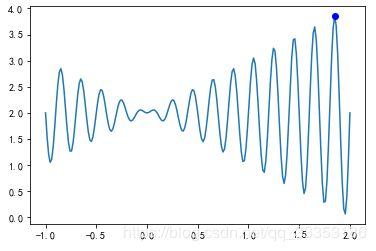
以一个非常简单的单目标优化问题为例:求f(x)=x*sin(10*pi*x)+2.0 在 x∈[-1,2] 上的最大值。
直接编写脚本如下:
"""demo.py"""
import numpy as np
import geatpy as ea # 导入geatpy库
import matplotlib.pyplot as plt
import time
"""============================目标函数============================"""
def aim(x): # 传入种群染色体矩阵解码后的基因表现型矩阵
return x * np.sin(10 * np.pi * x) + 2.0
x = np.linspace(-1, 2, 200)
plt.plot(x, aim(x)) # 绘制目标函数图像
"""============================变量设置============================"""
x1 = [-1, 2] # 自变量范围
b1 = [1, 1] # 自变量边界
varTypes = np.array([0]) # 自变量的类型,0表示连续,1表示离散
Encoding = 'BG' # 'BG'表示采用二进制/格雷编码
codes = [1] # 变量的编码方式,2个变量均使用格雷编码
precisions =[4] # 变量的编码精度
scales = [0] # 采用算术刻度
ranges=np.vstack([x1]).T # 生成自变量的范围矩阵
borders=np.vstack([b1]).T # 生成自变量的边界矩阵
"""=========================遗传算法参数设置========================="""
NIND = 40; # 种群个体数目
MAXGEN = 25; # 最大遗传代数
FieldD = ea.crtfld(Encoding,varTypes,ranges,borders,precisions,codes,scales) # 调用函数创建区域描述器
Lind = int(np.sum(FieldD[0, :])) # 计算编码后的染色体长度
obj_trace = np.zeros((MAXGEN, 2)) # 定义目标函数值记录器
var_trace = np.zeros((MAXGEN, Lind)) # 定义染色体记录器,记录每一代最优个体的染色体
"""=========================开始遗传算法进化========================"""
start_time = time.time() # 开始计时
Chrom = ea.crtbp(NIND, Lind) # 生成种群染色体矩阵
variable = ea.bs2real(Chrom, FieldD) # 对初始种群进行解码
ObjV = aim(variable) # 计算初始种群个体的目标函数值
best_ind = np.argmax(ObjV) # 计算当代最优个体的序号
# 开始进化
for gen in range(MAXGEN):
FitnV = ea.ranking(-ObjV) # 根据目标函数大小分配适应度值(由于遵循目标最小化约定,因此最大化问题要对目标函数值乘上-1)
SelCh=Chrom[ea.selecting('rws', FitnV, NIND-1), :] # 选择,采用'rws'轮盘赌选择
SelCh=ea.recombin('xovsp', SelCh, 0.7) # 重组(采用两点交叉方式,交叉概率为0.7)
SelCh=ea.mutbin(Encoding, SelCh) # 二进制种群变异
# 把父代精英个体与子代合并
Chrom = np.vstack([Chrom[best_ind, :], SelCh])
variable = ea.bs2real(Chrom, FieldD) # 对育种种群进行解码(二进制转十进制)
ObjV = aim(variable) # 求育种个体的目标函数值
# 记录
best_ind = np.argmax(ObjV) # 计算当代最优个体的序号
obj_trace[gen, 0] = np.sum(ObjV) / NIND # 记录当代种群的目标函数均值
obj_trace[gen, 1] = ObjV[best_ind] # 记录当代种群最优个体目标函数值
var_trace[gen, :] = Chrom[best_ind, :] # 记录当代种群最优个体的变量值
# 进化完成
end_time = time.time() # 结束计时
"""============================输出结果及绘图================================"""
best_gen = np.argmax(obj_trace[:, [1]])
print('目标函数最大值:', obj_trace[best_gen, 1]) # 输出目标函数最大值
variable = ea.bs2real(var_trace[[best_gen], :], FieldD) # 解码得到表现型
print('对应的决策变量值为:')
print(variable[0][0]) # 因为此处variable是一个矩阵,因此用[0][0]来取出里面的元素
print('用时:', end_time - start_time)
plt.plot(variable, aim(variable),'bo')
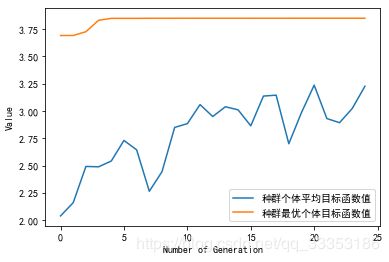
ea.trcplot(obj_trace, [['种群个体平均目标函数值', '种群最优个体目标函数值']])
运行结果如下:
目标函数最大值: 3.850272716105895
对应的决策变量值为:
1.8505813776055176
用时: 0.02496051788330078
仔细查看上述代码,我们会发现Geatpy的书写风格与Matlab大同小异,有Matlab相关编程经验的基本上可以无缝转移到Python上利用Geatpy进行遗传算法程序开发。
Geatpy提供了详尽的API文档,比如要查看上面代码中的"ranking"函数是干什么的,可以在python中执行
import geatpy as ga
help(ga.ranking)即可看到"ranking"函数的相关使用方法。
另外官网上也有更多详尽的Geatpy教程:http://geatpy.com/index.php/details/
2. 利用框架实现遗传算法。
Geatpy提供开放的面向对象进化算法框架。即“问题类”+“进化算法模板类+种群类”。对于一些复杂的进化算法,如多目标进化优化、改进的遗传算法等,按照上面所说的编写脚本代码是非常麻烦的,而用框架的方法可以极大提高编程效率。
这里给出一个利用框架实现NSGA-II算法求多目标优化函数ZDT-1的帕累托前沿面的例子:
第一步:首先编写ZDT1的问题类,写在“MyProblem.py”文件中:
# -*- coding: utf-8 -*-
"""MyProblem.py"""
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self):
name = 'ZDT1' # 初始化name(函数名称,可以随意设置)
M = 2 # 初始化M(目标维数)
maxormins = [1] * M # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
Dim = 30 # 初始化Dim(决策变量维数)
varTypes = [0] * Dim # 初始化varTypes(决策变量的类型,0:实数;1:整数)
lb = [0] * Dim # 决策变量下界
ub = [1] * Dim # 决策变量上界
lbin = [1] * Dim # 决策变量下边界
ubin = [1] * Dim # 决策变量上边界
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
def aimFunc(self, pop): # 目标函数
Vars = pop.Phen # 得到决策变量矩阵
ObjV1 = Vars[:, 0]
gx = 1 + 9 * np.sum(Vars[:, 1:30], 1)
hx = 1 - np.sqrt(ObjV1 / gx)
ObjV2 = gx * hx
pop.ObjV = np.array([ObjV1, ObjV2]).T # 把结果赋值给ObjV
def calReferObjV(self): # 计算全局最优解作为目标函数参考值
N = 10000 # 生成10000个参考点
ObjV1 = np.linspace(0, 1, N)
ObjV2 = 1 - np.sqrt(ObjV1)
globalBestObjV = np.array([ObjV1, ObjV2]).T
return globalBestObjV
上面代码中,问题类的构造函数__init__()是用于定义与ZDT1测试问题相关的一些参数,如决策变量范围、类型、边界等等。aimFunc()是待优化的目标函数。calReferObjV()用来计算理论的全局最优解,这个理论最优解可以是通过计算得到的,也可以是通过导入外部文件的数据得到的,如果待求解的问题没有或尚不知道理论最优解是多少,则这个calReferObjV()函数可以省略不写。
第二步:在同一个文件夹下编写执行脚本,实例化上述问题类的对象,然后调用Geatpy提供的nsga2算法的进化算法模板(moea_NSGA2_templet),最后结合理论全局最优解PF(即俗称的“真实前沿点”)通过计算GD、IGD、HV等指标来分析优化效果:
# -*- coding: utf-8 -*-
import geatpy as ea # import geatpy
from MyProblem import MyProblem
"""================================实例化问题对象============================="""
problem = MyProblem() # 生成问题对象
"""==================================种群设置================================"""
Encoding = 'RI' # 编码方式
NIND = 50 # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders) # 创建区域描述器
population = ea.Population(Encoding, Field, NIND) # 实例化种群对象(此时种群还没被初始化,仅仅是完成种群对象的实例化)
"""================================算法参数设置==============================="""
myAlgorithm = ea.moea_NSGA2_templet(problem, population) # 实例化一个算法模板对象`
myAlgorithm.MAXGEN = 200 # 最大进化代数
myAlgorithm.drawing = 1 # 设置绘图方式(0:不绘图;1:绘制结果图;2:绘制过程动画)
"""===========================调用算法模板进行种群进化===========================
调用run执行算法模板,得到帕累托最优解集NDSet。NDSet是一个种群类Population的对象。
NDSet.ObjV为最优解个体的目标函数值;NDSet.Phen为对应的决策变量值。
详见Population.py中关于种群类的定义。
"""
NDSet = myAlgorithm.run() # 执行算法模板,得到非支配种群
NDSet.save() # 把结果保存到文件中
# 输出
print('用时:%f 秒'%(myAlgorithm.passTime))
print('评价次数:%d 次'%(myAlgorithm.evalsNum))
print('非支配个体数:%d 个'%(NDSet.sizes))
print('单位时间找到帕累托前沿点个数:%d 个'%(int(NDSet.sizes // myAlgorithm.passTime)))
# 计算指标
PF = problem.getReferObjV() # 获取真实前沿,详见Problem.py中关于Problem类的定义
if PF is not None and NDSet.sizes != 0:
GD = ea.indicator.GD(NDSet.ObjV, PF) # 计算GD指标
IGD = ea.indicator.IGD(NDSet.ObjV, PF) # 计算IGD指标
HV = ea.indicator.HV(NDSet.ObjV, PF) # 计算HV指标
Spacing = ea.indicator.Spacing(NDSet.ObjV) # 计算Spacing指标
print('GD',GD)
print('IGD',IGD)
print('HV', HV)
print('Spacing', Spacing)
"""=============================进化过程指标追踪分析============================"""
if PF is not None:
metricName = [['IGD'], ['HV']]
[NDSet_trace, Metrics] = ea.indicator.moea_tracking(myAlgorithm.pop_trace, PF, metricName, problem.maxormins)
# 绘制指标追踪分析图
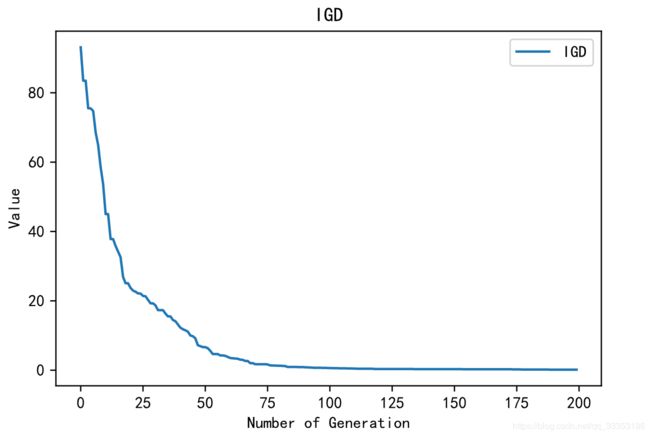
ea.trcplot(Metrics, labels = metricName, titles = metricName)
运行结果如下:
种群信息导出完毕。
用时:0.503653 秒
评价次数:10000 次
非支配个体数:50 个
单位时间找到帕累托前沿点个数:99 个
GD 0.0011025023611967554
IGD 0.15098973339777405
HV 0.624906599521637
Spacing 0.009326105831814594
正在进行进化追踪指标分析,请稍后......
指标追踪分析结束,进化记录器中有效进化代数为: 200
上述代码中已经对各个流程进行了详细的注释。其中进化算法的核心逻辑是写在进化算法模板内部的,可前往查看对应的源代码。此外,我们还可以参考Geatpy进化算法模板的源代码来自定义算法模板,以实现丰富多样的进化算法,如各种各样的改进的进化算法等:
最后值得注意的是:目标函数aimFunc()那一块地方最容易写错。aimFunc()的输入参数pop是一个种群对象(有关种群对象可以查看工具箱中的Population.py类源码,或者查看Geatpy数据结构)。pop.Phen是种群的表现型矩阵,意思是种群染色体解码后得到的表现型矩阵,它对应的即为问题类中的决策变量。Phen是一个矩阵,每一行对应种群中的一个个体的表现型。在计算目标函数时,可以把这个Phen拆成一行一行,即逐个逐个个体地计算目标函数值,然后再拼成一个矩阵赋值给pop对象的ObjV属性。也可以利用Numpy的矩阵化计算来“一口气”把种群所有个体的目标函数值计算出来。无论采用的是哪种计算方法,最后得到的目标函数值是要保存在pop对象的ObjV属性中的,这个ObjV是“种群目标函数值矩阵”,每一行对应一个个体的所有目标函数值,每一列对应一个目标。比如:
它表示有种群3个个体,待优化目标有2个。
后面的博客将深入理解Geatpy的数据结构、进化算法框架的用法与扩展,以及探讨框架的核心——进化算法模板的实现。还会讲一些使用Geatpy解决问题的案例。欢迎继续跟进~感谢!