Python机器学习——学习曲线

机器学习分为有监督学习和无监督的学习。

有监督学习：对数据的若干特征与若干标签之间的关联性进行建模的过程，确定模型后就能应用到新的未知数据中。进一步可以分为分类和回归任务。分类对应离散型数据，而回归对应的是连续性数据。SVM、随机森林和神经网络属于有监督的学习。

无监督学习：对不带任何标签的数据特征进行建模。包括聚类和降维，例如k-means算法等。

其中半监督学习介于二者之间，适用于数据标签不完整的情况。

Python机器学习主要调用模块为sklearn，里面有机器学习使用的各种模型算法以及评价指标。

进行数据分析、建模的过程一般为：读取数据—抽取样本，生成测试集和检验集—调用模型—模型预测—采用模型评价指标，评价模型预测结果

影响模型质量的两个因素为模型的复杂度以及训练集的规模。模型的学习曲线是指，训练集规模的训练得分/检验集的得分。

特征：

• 特定复杂度的模型对较小的数据集容易过拟合，此时训练集的得分较高，检验集的得分较低；
• 特定复杂度的模型对较大的数据集容易欠拟合；随着数据的增大，训练集得分会不断降低，检验集评分会不断升高；
• 模型的检验集得分永远不会高于训练集得分，两条曲线不断靠近，却不会交叉。

本次实验选取多项式模型，通过模型的多项式来提高或减少模型的复杂度，观察学习曲线的变化趋势。

（一）构造多项式回归模型，生成测试样本数据。

代码：

#构造多项式模型
from sklearn.preprocessing import PolynomialFeatures #专门产生多项式的工具并且包含相互影响的特征集
from sklearn.linear_model import LinearRegression #线性回归模型
from sklearn.pipeline import make_pipeline #构造管道

def PolynomialRegression(degree=2, **kwargs): #**kwargs 形参，返回值为字典类型
    return make_pipeline(PolynomialFeatures(degree),
                        LinearRegression(**kwargs))


#形成样本数据

import numpy as np

def make_data(N, err=1.0, rseed=1):
    #随机抽样数据
    rng = np.random.RandomState(rseed)
    X = rng.rand(N, 1) ** 2
    y = 10 - 1./ (X.ravel() + 0.1)
    if err > 0:
        y += err * rng.randn(N)
    return X, y
X, y = make_data(40)

（二）绘制多项式函数图像

绘制散点图，和几个多项式函数图像，观察多项式模型拟合效果。

代码：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn; seaborn.set() #设置图形样式

X_test = np.linspace(-0.1, 1.1, 500)[:, None]

plt.scatter(X.ravel(), y, color='black')
axis = plt.axis()
for degree in [1, 3, 5]:
    y_test = PolynomialRegression(degree).fit(X,y).predict(X_test)
    plt.plot(X_test.ravel(), y_test, label='degree={0}'.format(degree))
plt.xlim(-0.1, 1.0)
plt.ylim(-2, 12)
plt.legend(loc='best');

图形：

就该图形显示，三项式函数和五项式函数的模型拟合结果较为可观，一元线性函数的模型拟合效果较差。

（三）绘制学习曲线

观察训练得分和测试得分随着项式的增加，即随着模型复杂度的增加，训练得分和检验得分的变化情况。

代码：

from sklearn.learning_curve import validation_curve

degree = np.arange(0, 21)
train_score,val_score = validation_curve(PolynomialRegression(), X, y,
                                        'polynomialfeatures__degree',
                                        degree, cv=7)
plt.plot(degree, np.median(train_score, 1),color='blue', label='training score')
plt.plot(degree, np.median(val_score, 1), color='red', label='validation score')
plt.legend(loc='best')
plt.ylim(0, 1)
plt.xlabel('degree')
plt.ylabel('score')

图像：

 结果显示：随着模型复杂度的增加，训练得分（图中的蓝线部分）快速增加，达到饱和之后，增长幅度较低，趋于平缓；

测试得分（图中红色曲线）先增加，到达某一值后由于过拟合导致得分减少；

训练得分明显高于测试得分。该结果显示随着当模型复杂度到一定程度时，再增加模型的复杂度对模型的得分可能产生较小的影响或负影响，这个时候就会考虑更换模型。

（四）增加样本数量，观察模型拟合效果

在小数据的检验结果上得出，复杂度较高的模型，由于过拟合导致检验得分较低，所以测试，当增加样本数量时，学习曲线的变化情况。

代码：

X2, y2 = make_data(200) #生成200个数据样本
plt.scatter(X2.ravel(), y2)

#重新绘制学习曲线，并将小样本曲线添加上去

degree = np.arange(21)
train_score2, val_score2 = validation_curve(PolynomialRegression(), X2, y2,
                                           'polynomialfeatures__degree',
                                           degree, cv=7)

plt.plot(degree, np.median(train_score2, 1), color='blue',
        label='train score')
plt.plot(degree, np.median(val_score2, 1), color='red',
        label='validation score')
plt.plot(degree, np.median(train_score, 1),color='blue', alpha=0.3,
        linestyle='dashed')
plt.plot(degree, np.median(val_score, 1), color='red', alpha=0.3,
        linestyle='dashed')
plt.legend(loc='lower center')
plt.ylim(0, 1)
plt.xlabel('degree')
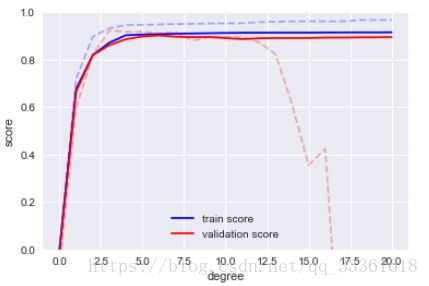
plt.ylabel('score')

图像：

 其中虚线代表小数据集的学习曲线，实线代表大数据集的学习曲线。

结论：大规模数据集的检验得分和测试得分的变化趋势一致，过拟合情况也不是很明显，说明大数据集适合用复杂程度较高的模型。