常用数据结构与排序算法实现、适用场景及优缺点(Java)
本笔记涉及代码:https://github.com/hackeryang/Algorithms-Fourth-Edition-Exercises
1.下压栈(后进先出)(能够动态调整数组大小的实现):
package Chapter1_3Text;
import java.util.Iterator;
public class ResizingArrayStack- implements Iterable
- { //下压栈的实现(后进先出)
private Item[] a=(Item[]) new Object[1]; //栈元素
private int N=0; //元素数量
public boolean isEmpty(){return N==0;}
public int size(){return N;}
private void resize(int max){
//将栈移动到一个大小为max的新数组
Item[] temp=(Item[]) new Object[max];
for(int i=0;i
0 && N==a.length/4) resize(a.length/2);
return item;
}
public Iterator- iterator(){
return new ReverseArrayIterator();
}
private class ReverseArrayIterator implements Iterator
- {
//支持后进先出的迭代
private int i=N;
public boolean hasNext(){return i>0;}
public Item next(){return a[--i];}
public void remove(){ }
}
}
2.下压堆栈(链表实现):
package Chapter1_3Text;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
import java.util.Iterator;
public class Stack- implements Iterable
- { //下压堆栈(链表实现)
private Node first; //栈顶(最近添加的元素)
private int N; //元素数量
private class Node{
//定义了节点的嵌套类
Item item;
Node next;
}
public boolean isEmpty(){return first==null;} //或:N==0
public int size(){return N;}
public void push(Item item){
//向栈顶添加元素
Node oldfirst=first;
first=new Node();
first.item=item;
first.next=oldfirst;
N++;
}
public Item pop(){
//从栈顶删除元素
Item item=first.item;
first=first.next;
N--;
return item;
}
//iterator()的实现在1.4节
public Iterator
- iterator(){
return new ListIterator();
}
private class ListIterator implements Iterator
- {
private Node current=first;
public boolean hasNext(){return current!=null;}
public void remove(){}
public Item next(){
Item item=current.item;
current=current.next;
return item;
}
}
public static void main(String[] args){
//创建一个栈并根据StdIn中的指示压入或弹出字符串
Stack
s=new Stack();
while(!StdIn.isEmpty()){
String item=StdIn.readString();
if(!item.equals("-"))
s.push(item);
else if(!s.isEmpty()) StdOut.print(s.pop()+" ");
}
StdOut.println("("+s.size()+" left on stack)");
}
}
3.先进先出队列:
package Chapter1_3Text;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
import java.util.Iterator;
public class Queue- implements Iterable
- { //先进先出队列
private Node first; //指向最早添加的节点的链接
private Node last; //指向最近添加的节点的链接
private int N; //队列中的元素数量
private class Node{
//定义了节点的嵌套类
Item item;
Node next;
}
public boolean isEmpty(){return first==null;} //或:N==0
public int size(){return N;}
public void enqueue(Item item){
//向表尾添加元素
Node oldlast=last;
last=new Node();
last.item=item;
last.next=null;
if(isEmpty()) first=last;
else oldlast.next=last;
N++;
}
public Item dequeue(){
//从表头删除元素
Item item=first.item;
first=first.next;
if(isEmpty()) last=null;
N--;
return item;
}
//iterator()的实现要到1.4节
public Iterator
- iterator(){
return new ListIterator();
}
private class ListIterator implements Iterator
- {
private Node current=first;
public boolean hasNext(){return current!=null;}
public void remove(){}
public Item next(){
Item item=current.item;
current=current.next;
return item;
}
}
public static void main(String[] args){
//创建一个队列并操作字符串入列或出列
Queue
q=new Queue();
while(!StdIn.isEmpty()){
String item=StdIn.readString();
if(!item.equals("-"))
q.enqueue(item);
else if(!q.isEmpty()) StdOut.print(q.dequeue()+" ");
}
StdOut.println("("+q.size()+" left on queue)");
}
}
4.背包:
package Chapter1_3Text;
import java.util.Iterator;
public class Bag- implements Iterable
- { //背包
private Node first; //链表的首节点
private class Node{
Item item;
Node next;
}
public void add(Item item){
//和Stack的push()方法完全相同
Node oldfirst=first;
first=new Node();
first.item=item;
first.next=oldfirst;
}
public Iterator
- iterator(){
return new ListIterator();
}
private class ListIterator implements Iterator
- {
private Node current=first;
public boolean hasNext(){return current!=null;}
public void remove(){}
public Item next(){
Item item=current.item;
current=current.next;
return item;
}
}
}
5.比较两种排序算法运行时间快慢的方法:
package Chapter2_1Text;
import edu.princeton.cs.algs4.*;
import edu.princeton.cs.algs4.Selection;
public class SoftCompare { //比较两种排序算法运行时间快慢的方法
public static double time(String alg,Double[] a){
Stopwatch timer=new Stopwatch();
if(alg.equals("Insertion")) Insertion.sort(a);
if(alg.equals("Selection")) Selection.sort(a);
if(alg.equals("Shell")) Shell.sort(a);
if(alg.equals("Merge")) Merge.sort(a);
if(alg.equals("Quick")) Quick.sort(a);
if(alg.equals("Heap")) Heap.sort(a);
return timer.elapsedTime();
}
public static double timeRandomInput(String alg,int N,int T){
//使用算法alg将T个长度为N的数组排序
double total=0.0;
Double[] a=new Double[N];
for(int t=0;t6.选择排序,算法的时间效率取决于比较的次数:
package Chapter2_1Text;
public class Selection { //选择排序,算法的时间效率取决于比较的次数
public static void sort(Comparable[] a){
//将a[]按升序排列
int N=a.length; //数组长度
for(int i=0;i对于长度为N的数组,选择排序需要大约(N^2)/2次比较和N次交换,数组元素交换位置的次数和数组的大小是线性关系。
7.插入排序,给要插入的元素腾出空间,将其余所有元素在插入之前都向右移动一位:
package Chapter2_1Text;
import edu.princeton.cs.algs4.In;
public class Insertion { //插入排序,给要插入的元素腾出空间,将其余所有元素在插入之前都向右移动一位
public static void sort(Comparable[] a){
//将a[]按升序排列
int N=a.length;
for(int i=1;i0 && less(a[j],a[j-1]);j--)
exch(a,j,j-1);
}
}
private static boolean less(Comparable v,Comparable w){return v.compareTo(w)<0;}
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
public static boolean isSorted(Comparable[] a){
//测试数组元素是否有序
for(int i=1;i 与选择排序不同,插入排序所需的时间取决于输入的元素的初始顺序。对于随机排列的长度为N且主键不重复的数组,平均情况下插入排序需要约(N^2)/4次比较以及大约(N^2)/4次交换。最坏情况下需要约(N^2)/2次比较和约(N^2)/2次交换,最好情况下需要N-1次比较和0次交换。
8.插入排序对部分有序的数组很有效,但是选择排序不然。当顺序倒置的元素数量很少时,插入排序比其他排序算法都要快。插入排序需要的交换操作和数组中元素大小顺序倒置的数量相同,需要的比较次数大于等于倒置的数量,小于等于倒置的数量加上数组的大小再减一。由于插入排序不会移动比插入的元素更小的元素,所需的比较次数平均只有选择排序的一半。
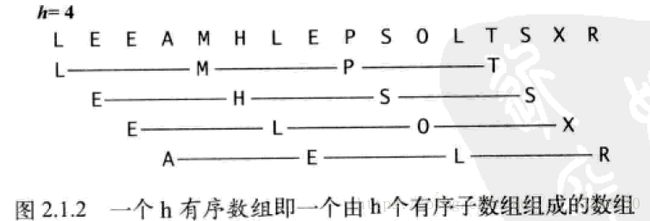
9.希尔排序,在插入排序中加入一个外循环来以h为间隔,按照递增序列递减得到:
package Chapter2_1Text;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;
public class Shell { //希尔排序,在插入排序中加入一个外循环来以h位为间隔排序,不断递减间隔h最终间隔为1,使所有元素都有序
public static void sort(Comparable[] a){
//将a[]按升序排列
int N=a.length;
int h=1;
while(h=1){
//将数组变为每隔h位有序
for(int i=h;i=h && less(a[j],a[j-h]);j-=h)
exch(a,j,j-h);
}
h=h/3;
}
}
private static boolean less(Comparable v,Comparable w){return v.compareTo(w)<0;}
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
public static boolean isSorted(Comparable[] a){
//测试数组元素是否有序
for(int i=1;i 该算法的性能不仅取决于每个排序子数组的间隔h,还取决于h之间的数学性质,如公因子等。希尔排序比插入排序和选择排序要快得多,并且数组越大,优势越大。它的运行时间复杂度达不到平方级别。在最坏的情况下,上面的实现(h以三倍来变化)的比较次数和N^(3/2)成正比。
10.对于中等大小的数组,希尔排序的运行时间是可以接受的。它的代码量不大,也不需要使用额外的内存空间。除非对于很大的N,其他更高效的算法可能只会比希尔排序快两倍甚至不到,而且代码更复杂,如果需要解决一个排序问题而又没有系统排序函数可用(例如直接接触硬件或者运行于嵌入式系统中的代码),可以先用希尔排序,再考虑是否替换为更复杂的排序算法。而对于部分有序和小规模的数组,应使用插入排序。
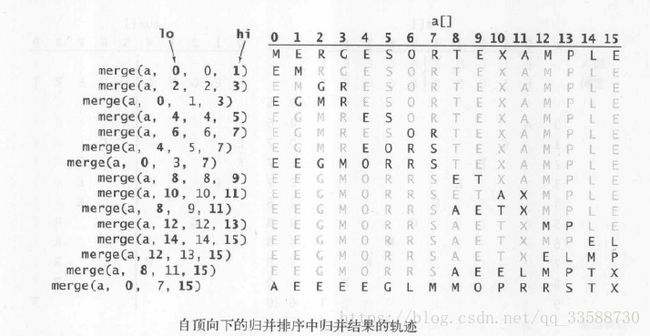
11.自顶向下的归并排序,先将所有元素复制到aux[]中,然后再归并回a[]中:
package Chapter2_2Text;
public class Merge { //自顶向下的归并排序,先将所有元素复制到aux[]中,然后再归并回a[]中
private static Comparable[] aux; //归并所需的辅助数组
public static void sort(Comparable[] a){
aux=new Comparable[a.length]; //一次性分配空间,这里必须要初始化容量为a.length,否则下面for循环k<=hi情况下递增到最后会报错NullPointerException
sort(a,0,a.length-1);
}
private static void sort(Comparable[] a,int lo,int hi){
//将数组a[lo..hi]排序
if(hi<=lo) return;
int mid=lo+(hi-lo)/2; //也可以int mid=(lo+hi)>>1,二进制中按位向右移一位等同于除以2
sort(a,lo,mid); //递归将数组左半边排序
sort(a,mid+1,hi); //递归将数组右半边排序
merge(a,lo,mid,hi); //归并左右半边的结果
}
public static void merge(Comparable[] a,int lo,int mid,int hi){
//将a[lo..mid]和a[mid+1..hi]归并
int i=lo,j=mid+1; //设置两个分别从数组头部和中间位置开始的两个游标,将数组分为左右两半进行归并比较
for(int k=lo;k<=hi;k++)
aux[k]=a[k]; //将辅助数组填满原数组原来顺序的元素,因为最后原数组会被填入排序过的元素
for(int k=lo;k<=hi;k++){
//归并回到a[lo..hi]
if(i>mid) a[k]=aux[j++]; //左半边用尽,取右半边的元素
else if(j>hi) a[k]=aux[i++]; //右半边用尽,取左半边的元素
else if(less(aux[j],aux[i])) a[k]=aux[j++]; //出现逆序的数字对,右半边的当前元素小于左半边的当前元素,取右半边的元素
else a[k]=aux[i++]; //右半边的当前元素大于左半边的当前元素,取左半边的元素
}
}
private static boolean less(Comparable v,Comparable w){return v.compareTo(w)<0;}
}
归并排序是算法设计中分治思想的典型应用,对于长度为N的任意数组,自顶向下的归并排序需要1/2*NlgN至NlgN次比较,最多需要访问数组6NlgN次。所以,归并排序所需的时间和NlgN成正比,可以用归并排序处理数百万甚至更大规模的数组,但是插入排序和选择排序做不到。归并排序的主要缺点是辅助数组所使用的额外空间和N的大小成正比。
12.自底向上的归并排序,多次遍历整个数组,根据子数组大小进行两两归并,四四归并,八八归并一直下去。每下一轮中子数组的大小会翻倍:
package Chapter2_2Text;
public class MergeBU { //自底向上的归并排序
private static Comparable[] aux; //归并所需的辅助数组,多次遍历整个数组,根据子数组大小进行两两归并,四四归并,八八归并一直下去。每下一轮中子数组的大小会翻倍
public static void merge(Comparable[] a,int lo,int mid,int hi){
//将a[lo..mid]和a[mid+1..hi]归并
int i=lo,j=mid+1;
for(int k=lo;k<=hi;k++) //将a[lo..hi]复制到aux[lo..hi]
aux[k]=a[k];
for(int k=lo;k<=hi;k++){
//归并回到a[lo..hi]
if(i>mid) a[k]=aux[j++]; //左半边用尽,取右半边的元素
else if(j>hi) a[k]=aux[i++]; //右半边用尽,取左半边的元素
else if(less(aux[j],aux[i])) a[k]=aux[j++]; //右半边的当前元素小于左半边的当前元素,取右半边的元素
else a[k]=aux[i++]; //右半边的当前元素大于左半边的当前元素,取左半边的元素
}
}
private static boolean less(Comparable v,Comparable w){return v.compareTo(w)<0;}
public static void sort(Comparable[] a){
//进行lgN次两两归并
int N=a.length;
aux=new Comparable[N];
for(int sz=1;sz对于长度为N的任意数组,自底向上的归并排序需要1/2NlgN至NlgN次比较,最多访问数组6NlgN次。自底向上的归并排序比较适合用链表组织的数据。这种方法只需要重新组织链表链接就能将链表原地排序,不需要创建任何新的链表节点,不像前面几种排序需要额外创建辅助数组。自顶向下的归并排序是化整为零,然后递归解决的方式,而自底向上的归并排序是用循序渐进的方式来解决。
13.任何基于比较的算法将长度为N的数组排序需要lg(N!)~NlgN次比较,在二叉树中,高度为h的树,叶子节点的数量为N!~2^h个。所以,归并排序在最坏情况下的比较次数约为NlgN。归并排序是一种渐近最优的基于比较排序的算法。
14.快速排序的步骤:
(1)先将输入的数组随机打乱。
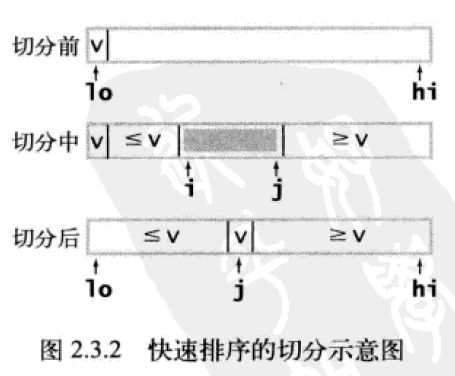
(2)将一个数组切分成两个子数组,左边子数组元素都不大于中间元素,右边子数组元素都不小于中间元素。即切分位置a[j]的条件是,a[lo]到a[j-1]中所有元素都不大于a[j],而且a[j+1]到a[hi]中的所有元素都不小于a[j],切分的具体实现是:将a[lo]作为初始切分元素,从数组的左端向右扫描直到找到一个大于等于a[lo]的元素a[i],再从数组右端向左扫描到一个小于等于a[lo]的元素a[j],然后将a[i]和a[j]交换位置,如此继续,直到i和j两个指针相遇(两个指针还未交错),在两指针交错后就将a[lo]与a[j]交换位置,一开始的a[lo]现在变成了a[j],在两个指针相遇交错前的位置i上,这个元素就是中间的切分元素。
(3)继续递归,将上一轮的中间切分元素a[j](值是一开始的a[lo])的前一个值a[j-1]作为新一轮切分的a[hi],再如(2)的规则切分,如此循环直到第一轮切分的中间切分元素a[j]的左边都已经被排序。
(4)接着从第一轮切分后的中间切分元素a[j]的右边开始快速排序,也就是将当时的a[j+1]作为右边第一次切分的a[lo],继续切分,过程和(3)相同,最后第一轮切分的a[j]的左边和右边都已经有序,快速排序完成。
具体代码实现如下:
package Chapter2_3Text;
import edu.princeton.cs.algs4.Insertion;
import edu.princeton.cs.algs4.StdRandom;
public class Quick { //快速排序算法(重要)
public static void sort(Comparable[] a){
StdRandom.shuffle(a); //把数组打乱,消除对输入的依赖
sort(a,0,a.length-1);
}
private static void sort(Comparable[] a,int lo,int hi){
int M=10; //转换参数M的最佳值与系统有关,但5到15的任意值在大多数情况下都行
if(hi<=lo+M){
Insertion.sort(a,lo,hi); //对于小数组,快速排序比插入排序慢
return;
}
int j=partition(a,lo,hi); //切分成两个子数组
sort(a,lo,j-1); //将左半部分a[lo.j-1]排序
sort(a,j+1,hi); //将右半部分a[j+1..hi]排序
}
private static int partition(Comparable[] a,int lo,int hi){
//将数组切分为a[lo..i-1],a[i],a[i+1..hi]
int i=lo,j=hi+1; //向右向左的扫描指针,j为hi+1,这样从右到左扫描会先从hi开始扫描
Comparable v=a[lo]; //切分元素初始化为第一个元素,且该v以后为定值,就是最初的a[lo],以后a[lo]的值如何改变都与v无关
while(true){
//扫描左右两侧,检查扫描是否结束并交换元素
while(less(a[++i],v)) if(i==hi) break;
while(less(v,a[--j])) if(j==lo) break;
if(i>=j) break;
exch(a,i,j);
}
exch(a,lo,j); //将v=a[j]放入正确的位置,当扫描指针i和j相遇时,将a[j]与a[lo]交换
return j; //a[lo..j-1]<=a[j]<=a[j+1..hi]达成
}
private static boolean less(Comparable v,Comparable w){return v.compareTo(w)<0;}
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
}
在循环中,a[i]小于一开始的a[lo]的值v时增大i,a[j]大于v时减小j(注意v是定值不再变化),然后交换a[i]和a[j]来保证i左侧的元素都不大于v,j右侧的元素都不小于v,当扫描指针相遇或交错后交换a[lo]和a[j],切分结束,这样切分的中间值就是a[j]。快速排序的通俗理解图例如下:
15.快速排序与归并排序的比较:快速排序的优点是原地排序(只需要一个很小的辅助栈),且将长度为N的数组排序所需的时间和NlgN成正比。快速排序也是一种分治的排序算法,将一个数组切分成两个子数组,将两部分独立的排序,与归并排序彼此互补。归并排序将数组分成两个子数组分别排序,并将有序的子数组归并以将整个数组排序;而快速排序将数组排序的方式则是当两个子数组都有序时整个数组也就自然有序了。在归并排序中,递归调用发生在处理整个数组之前,而快速排序中,递归调用发生在处理整个数组之后。在归并排序中,一个数组被等分为两半,而在快速排序中,切分的位置取决于数组的内容。对于含有以任意概率分布的重复元素的输入,归并排序无法保证最佳性能。
16.快速排序的优缺点:原地排序,只需要一个很小的辅助栈,将长度为N的数组排序所需的时间和NlgN成正比。归并排序和希尔排序一般都比快速排序慢,因为前两者还在内循环中移动数据。快速排序的另一个速度优势在于比较次数较少。但是,该实现有个潜在的缺点:在切分不平衡时该程序会极为低效,可能会使性能达到平方级别。快速排序最多需要约(N^2)/2次比较,但一开始的随机打乱数组可以预防这种情况。但是,对于小数组,快速排序比插入排序慢。
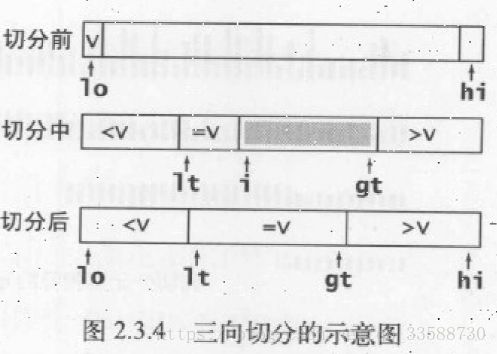
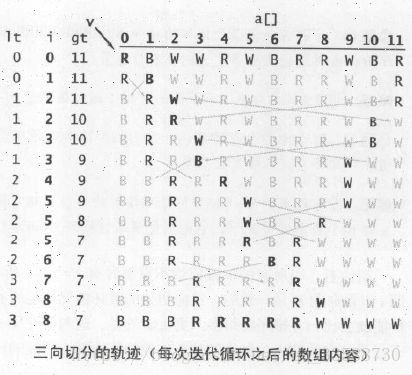
17.三向切分的快速排序,是从左到右遍历数组一次,维持一个指针lt使a[lo..lt-1]中的元素都小于v=a[lo],一个指针gt使a[gt+1..hi]中的元素都大于v,一个指针i使a[lt..i-1]中的元素都等于v,而a[i..gt]中的元素还未确定。一开始i和lo相等,对a[i]进行以下比较及处理:
(1)a[i]小于v,将a[lt]和a[i]交换,将lt和i加一。
(2)a[i]大于v,将a[gt]和a[i]交换,将gt减一。
(3)a[i]等于v,将i加一。
这些操作会不断缩小gt-i的值,因此除非和切分元素相等,其他元素都会被交换。
实现如下:
package Chapter2_3Text;
import edu.princeton.cs.algs4.StdRandom;
//三向切分的快速排序,是从左到右遍历数组一次,维持一个指针lt使a[lo..lt-1]中的元素都小于a[lo],一个指针gt使a[gt+1..hi]中的元素都大于a[lo],一个指针i使a[lt..i-1]中的元素都等于a[lo],而a[i..gt]中的元素还未确定。
public class Quick3way {
public static void sort(Comparable[] a){
StdRandom.shuffle(a); //将数组内元素打乱顺序
sort(a,0,a.length-1);
}
private static void sort(Comparable[] a,int lo,int hi){
if(hi<=lo) return;
int lt=lo,i=lo+1,gt=hi;
Comparable v=a[lo]; //这边v为定值,不再随循环中的a[lo]变化
while(i<=gt){
int cmp=a[i].compareTo(v);
if(cmp<0) exch(a,lt++,i++);
else if(cmp>0) exch(a,i,gt--);
else i++;
} //现在a[lo..lt-1]对于存在大量重复元素的数组,这种方法比标准快速排序的效率高得多。
18.最小优先队列,优先删除最小的元素,留下最大的多个元素,例如在银行交易中,显示交易数额最大的用户信息:
package Chapter2_4Text;
import edu.princeton.cs.algs4.*;
public class TopM { //最小优先队列,留下最大的,删掉最小的
public static void main(String[] args){
//打印输入流中最大的M行
int M=Integer.parseInt(args[0]);
MinPQ pq=new MinPQ(M+1); //优先队列的容量为M+1,只存最大的这么多个元素
while(StdIn.hasNextLine()){
//为下一行输入创建一个元素并放入优先队列中
pq.insert(new Transaction(StdIn.readLine()));
if(pq.size()>M)
pq.delMin(); //如果优先队列中存在M+1个元素则删除其中最小的元素,如果新加入的元素最小也会被删掉
} //最大的M个元素都在优先队列中
Stack stack=new Stack();
while(!pq.isEmpty()) stack.push(pq.delMin()); //栈中存放顺序是最小优先队列中,较小的先push进来放在栈底,最大的在栈顶
for(Transaction t:stack) StdOut.println(t); //因为上一行的存放方式,较大元素在栈顶所以先被输出
}
}
优先队列适合总数据量太大,无法排序甚至无法全部装进内存的场合,例如10亿个元素中选出最大的10个,只需要一个能存储10个元素的队列即可。优先队列不是线程安全的,入队和出队的时间复杂度是 O(log(n)) 。
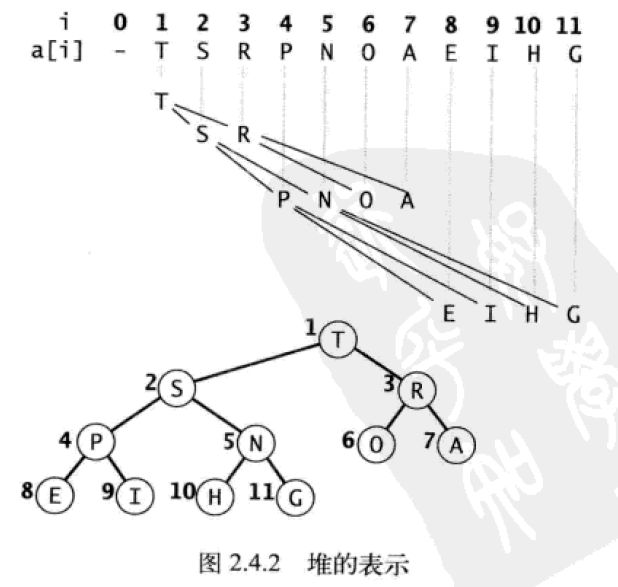
19.二叉树/二叉堆。在二叉堆数组中,每个元素都大于等于另两个特定位置的元素,当一棵二叉树的每个节点都大于等于它的两个子节点时,被称为堆有序。根节点是堆有序的二叉树中的最大节点。堆有序的二叉树称为完全二叉树,可以通过数组来表示,但不使用数组的第一个位置(即0),根节点从第二个位置,也就是1开始,具体方法就是将二叉树的节点按照层级顺序放入数组中,根节点的子节点在位置2和3,子节点的子节点分别在位置4,5,6,7,以此类推,如下所示:
因此,位置k的节点的父节点的位置为k/2,而它两个子节点的位置为2k和2k+1。基于二叉堆的最大优先队列实现如下:
package Chapter2_4Text;
public class MaxPQ> { //基于二叉堆的最大优先队列,优先踢出最大元素
private Key[] pq; //基于堆的完全二叉树,每个节点都大于等于它的两个子节点
private int N=0; //存储于pq[1..N]中,pq[0]没有使用
public MaxPQ(int maxN){pq=(Key[])new Comparable[maxN+1];}
public boolean isEmpty(){return N==0;}
public int size(){return N;}
public void insert(Key v){
pq[++N]=v;
swim(N); //从二叉树的末尾插入元素,并根据插入元素的大小上浮至合适的层级
}
public Key delMax(){
Key max=pq[1]; //从根节点得到最大元素
exch(1,N--); //将其和最后一个节点交换
pq[N+1]=null; //删除交换到最后一个元素的原根节点,并防止对象游离,这里的N+1其实就是上一行的N,只不过上一行已经将N的大小减一,将引用指向了原来最后一个元素的前一个元素
sink(1); //原来最后一个元素插入到了树的根节点处,根据元素大小下沉至合适的层级
return max;
}
private boolean less(int i,int j){return pq[i].compareTo(pq[j])<0;}
private void exch(int i,int j){
Key t=pq[i];
pq[i]=pq[j];
pq[j]=t;
}
private void swim(int k){
while(k>1 && less(k/2,k)){
exch(k/2,k);
k=k/2;
}
}
private void sink(int k){ //堆的有序状态因为某个节点变得比它的两个子节点或者其中之一更小而打破,则将它和它的两个子节点中较大者进行交换
while(2*k<=N){
int j=2*k; //找到k的下一层子节点
if(j 对于一个含有N个元素的基于二叉堆的优先队列,插入元素操作只需不超过(lgN+1)次比较,删除最大元素操作需要不超过2lgN次比较。用二叉堆实现的优先队列在现代应用程序中越来越重要,因为它能在插入操作和删除最大元素操作混合的动态场景中保证对数级别的运行时间。
20.堆排序,一开始将原始数组重新组织安排进一个二叉堆中,然后进行下沉排序,从二叉堆中按递减顺序不断重复取出并删除最大元素,该排序方法的优点是在排序时可以将需要排序的数组本身作为堆,无需任何额外空间:
package Chapter2_4Text;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class HeapSort {
//堆排序,一开始将原始数组重新组织安排进一个二叉堆中,然后进行下沉排序,从二叉堆中按递减顺序不断重复取出并删除最大元素
public static void sort(Comparable[] a){
int N=a.length;
for(int k=N/2;k>=1;k--) //从底部倒数第二层开始下沉交换
sink(a,k,N);
while(N>1){
exch(a,1,N--); //将当前N减小,当前的N后面的最大元素都已有序并被排除出二叉堆,因此只排序N前面的元素
sink(a,1,N);
}
}
private static boolean less(Comparable[] a,int i,int j){return a[i-1].compareTo(a[j-1])<0;}
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i-1]; //因为二叉堆的索引是1到N,而一般数组是0到N-1,为了与其他排序算法实现一致而减一,即将a[0]至a[N-1]排序
a[i-1]=a[j-1];
a[j-1]=t;
}
private static void sink(Comparable[] a,int k,int N){
while(2*k<=N){
int j=2*k;
if(j通俗理解的过程图如下:
堆排序的过程与选择排序有些类似(按照降序而非升序取出所有元素),但所需的比较要少得多,因为二叉堆提供了一种从未排序部分找到最大元素的有效方法。将N个元素排序,堆排序只需少于(2NlgN+2N)次比较,以及一半次数的交换。堆排序适合例如嵌入式系统或低成本移动设备中容量有限的场景,但很少应用于现代系统的很多应用中,因为它无法利用缓存,数组元素很少和相邻其他元素比较,因此缓存未命中的次数远远高于大多数比较都在相邻元素间进行的算法,如快速排序,归并排序,希尔排序。
21.在很多应用中都会需要将一组对象根据含有的几个不同属性,来进行对应的排序,例如Transaction对象中含有客户名称,日期和交易金额,有时需要按金额大小排序,有时可能需要按照另一个属性来排序,一个元素(对象)的多种属性都可能被用作排序的键。要实现这种根据不同属性各自排序的灵活性,Comparator接口正合适,可以通过定义多种比较器来完成,例如:
package Chapter2_5Text;
import edu.princeton.cs.algs4.Date;
import java.util.Comparator;
public class Transaction { //根据金融交易的不同属性自定义比较器
private String who;
private Date when;
private double amount;
public static void sort(Object[] a,Comparator c){ //在参数c中传入多种Comparator可以实现针对对象的不同属性进行排序的方法,例如传入下方的new Transaction.WhenOrder()
int N=a.length;
for(int i=1;i0 && less(c,a[j],a[j-1]);j--)
exch(a,j,j-1);
}
private static boolean less(Comparator c,Object v,Object w){return c.compare(v,w)<0;}
private static void exch(Object[] a,int i,int j){
Object t=a[i];
a[i]=a[j];
a[j]=t;
}
public static class WhenOrder implements Comparator{ //根据日期进行排序的比较器
public int compare(Transaction v,Transaction w){return v.when.compareTo(w.when);}
}
public static class HowMuchOrder implements Comparator{ //根据金额大小进行排序的比较器
public int compare(Transaction v,Transaction w){
if(v.amountw.amount) return +1;
else return 0;
}
}
}
这样定义之后,需要将Transaction对象的数组按照时间排序可以调用Transaction.sort(a, new Transaction.WhenOrder()),或者按照金额排序可以使用Transaction.sort(a, new Transaction.HowMuchOrder())。
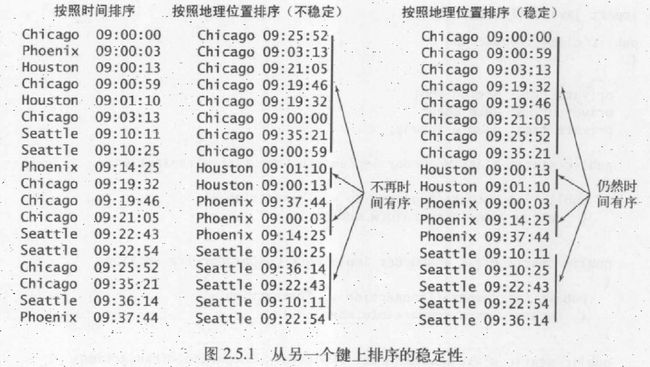
22.如果一个排序算法能够保持数组中重复元素的相对顺序位置则可以认为是稳定的,例如相同地名下时间依然按照先后顺序排列而不是打乱。上述算法中,插入排序和归并排序是稳定的,但是选择排序、希尔排序、快速排序和堆排序不是。稳定性的通俗描述如下图所示:
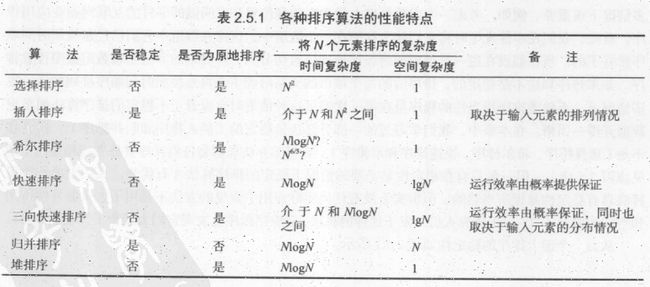
23.除了希尔排序(复杂度只是一个近似值)、插入排序(复杂度取决于输入元素的排列情况)和上面快速排序的两个版本(复杂度和概率有关,取决于输入元素的分布状况)之外,将其他排序算法的运行时间的增长数量级乘以适当的常数就能大致估计出运行时间。各种排序算法的性能特点如下所示:
24.在大多数实际情况中,快速排序是最佳选择。快速排序之所以是最快的通用排序算法是因为它的内循环中指令很少,而且还能利用缓存,因为它总是顺序地访问数据。所以它的运行时间增长数量级为约cNlgN,这里的c比其他线性对数级别的排序算法的相应常数都要小。在使用三向切分快速排序后,对于实际应用中可能出现的某些分布的输入就变成线性级别的了,而其他排序算法依然需要线性对数时间。但是,如果稳定性很重要而空间充足,归并排序是最好的选择。而在运行时间至关重要的任何排序应用中,应考虑使用快速排序。对于Java来说,会对原始数据类型使用三向切分的快速排序,而对引用类型使用归并排序。这些选择实际上也表示了用速度和空间(对于原始数据类型)来换取稳定性(对于引用类型)。
25.找到一组数中第k小的元素:
package Chapter2_5Text;
import edu.princeton.cs.algs4.StdRandom;
public class KthSmallest {
//找到一组数中的第k小元素
public static Comparable select(Comparable[] a,int k){
StdRandom.shuffle(a);
int lo=0,hi=a.length-1;
while(hi>lo){
int j=partition(a,lo,hi);
if(j==k) return a[k]; //切分之后,a[j]左边的数小于等于a[j],右边的数大于等于a[j],如果j碰巧等于k,则该a[j]就是第k小的数
else if(j>k) hi=j-1;
else if(j=j) break;
exch(a,i,j);
}
exch(a,lo,j); //将v=a[j]放入正确的位置,当扫描指针i和j相遇时,将a[j]与a[lo]交换
return j; //a[lo..j-1]<=a[j]<=a[j+1..hi]达成
}
private static boolean less(Comparable v,Comparable w){return v.compareTo(w)<0;}
private static void exch(Comparable[] a,int i,int j){
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
}
在快速排序的切分操作中,如果k