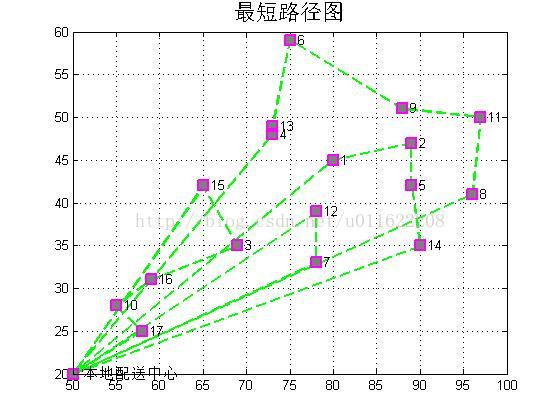
蚁群算法求解有时间窗约束的车辆路径问题matlab程序

有时间窗车辆路径问题 

 

有时间窗车辆路径问题(vehicle routing problems with time windows，VRPTW)车辆路线问题(VRP)最早是由Dantzig和Ramser于1959年首次提出，它是指一定数量的客户，各自有不同数量的货物需求，配送中心向客户提供货物，由一个车队负责分送货物，组织适当的行车路线，目标是使得客户的需求得到满足，并能在一定的约束下，达到诸如路程最短、成本最小、耗费时间最少等目的。

理论依据

由于VRP问题的持续发展，考虑需求点对于车辆到达的时间有所要求之下，在车辆途程问题之中加入时窗的限制，便成为有时间窗车辆路径问题(VRP with Time Windows, VRPTW)。有时间窗车辆路径问题(VRPTW)是在VRP上加上了客户的被访问的时间窗约束。在VRPTW问题中，除了行驶成本之外, 成本函数还要包括由于早到某个客户而引起的等待时间和客户需要的服务时间。

在VRPTW中，车辆除了要满足VRP问题的限制之外，还必须要满足需求点的时窗限制，而需求点的时窗限制可以分为两种，一种是硬时窗(Hard Time Window)，硬时窗要求车辆必须要在时窗内到达，早到必须等待，而迟到则拒收;另一种是软时窗(Soft Time Window)，不一定要在时窗内到达，但是在时窗之外到达必须要处罚，以处罚替代等待与拒收是软时窗与硬时窗最大的不同。

Bodin和Solomon分别对VRP及其变形问题和VRPTW问题作了较详细的综述。生产实际中许多问题都可以归结为VRPTW来处理, 如钢铁厂编制热轧带钢轧制计划问题实际上就是一个VRPTW问题。一些服务性行业中也普遍存在这样的问题, 如邮政投递，飞机、火车及公共汽车的调度等。自从Savelsbergh证明了VRPTW是一个NP难问题之后, 对其算法的研究就主要集中到各种启发式算法上。遗传算法、禁忌搜索法和模拟退火法等智能化启发式算法的出现为求解VRPTW问题提供了新的工具。Thangiah和Joe都曾应用遗传算法求解VRPTW问题, 前者的目标是使总的服务成本最小, 而后者的目标有两个, 首先是使用最少的车辆, 其次是在使用最少车辆的前提下使总成本最小。

求解方法

含时窗限制之车辆途程问题(VRPTW)相对于车辆途程问题(VRP)，必须额外考虑到运送时间与时间窗口，其主要的原因来自顾客有服务时间的最后期限和最早开始服务时间的限制。故在此限制条件之下，原本VRP问题除了空间方面的路径(Routing)考虑之外，还必须要加上时间上的排程(Scheduling)考虑。同时由于场站也有时间窗的限制，也间接造成路径长度的限制，由此可知VRPTW的总巡行成本不仅包含运送成本，还需要考虑时间成本，以及未在时间窗限制内送达的处罚成本。因此，若要得到一个好的解答，时间和空间(Temporal andSpatial)问题的探讨是非常重要的。

由于VRPTW比VRP问题多考虑了一样时窗的因素，因此在解法上较VRP问题更为复杂，而根据Taillard(1997)等人的分类，求解VRPTW的方法可以分为六种，分述如下。

分枝界限法

以分枝界限法求算之精确解法(Exact Algorithm Based on Branch-and-BoundTechniques):Kolen(1987)利用这种方式可以求得精确解，但是只能解决六至十五个节点的问题，因此求解的范围过小，仅适用于小型问题。

途程建构启发

途程建构启发式算法(Route Construction Heuristics):在一问题中，以某节点选择原则或是路线安排原则，将需求点一一纳入途程路线的解法。如Soloman(1987)的循序建构法(Sequential Insertion Heuristics)。

途程改善启发

途程改善启发式算法(Route Improvement Heuristics):先决定一个可行途程，也就是一个起始解，之后对这个起始解一直做改善，直到不能改善为止。而常见的是节线交换法(Edge Exchange Procedure)，如Lin(1965)所提出的K-Optimal，以及Potvin与Rousseau(1993)提出一考虑旅行方向的交换算法。

合成启发

合成启发式算法(Composite Heuristics):此种解法混合了途程建构启发式算法与途程改善启发式算法，如Russell(1995)所提出的Hybrid Heuristics便是混合了Potvin与Rousseau(1993)所提出的平行插入法，并在之中加入路线改善法的合成启发式算法;Roberto(2000)也提出的属于平行插入法与内部交换改善法的合成启发式解法来求解VRPTW的问题。

依据最佳化

依据最佳化之启发式算法(Optimization-Based Heuristics):如Koskosidis(1992)等人利用混合整数规划模块，再透过启发式算法，将原始问题分解成指派/分群的子问题的一系列的巡行以及排程问题。

通用启发

通用启发式算法(Metaheuristics):传统区域搜寻方法的最佳解常因起始解的特性或搜寻方法的限制，而只能获得局部最佳解，为了改善此一缺点，近年来在此领域有重大发展，是新一代的启发式解法，包含禁忌法(Tabu Search)、模拟退火法(Simulated Annealing)、遗传算法(Genetic Algorithm)和门坎接受法(Threshold Accepting)等，可以有效解决局部最佳化的困扰。如Potvin(1996)等人、Taillard(1997)等人均利用Tabu Search的方式来求解VRPTW的问题。

1 简介

带时间窗的车辆路径问题(VRPTW)一般描述为从某一物流配送中心出发，用多台车辆向多个顾客送货，车辆完成配送任务后返回配送中心。 已知每个顾客的位置与需求量， 每台车的容量一定， 将货物送到顾客手中需要满足一定的时间约束， 要求合理安排行车路线使目标函数得到优化。 对该问题的研究引起了广大学者的关注。 它是有容量约束车辆路径问题的扩展， 是NP难题， 求解算法可分为精确算法与启发式算法。当顾客点数目较多时， 使用精确算法很难在可接受的时间内求得全局最优解， 因此， 用启发式算法在可接受的时间内求得问题的满意解成为研究的重要方向。

蚁群算法是由Dorigo等首先提出来的， 它的基本思想是利用一群人工蚂蚁的协作来寻找优化问题的较优解， 每只蚂蚁根据问题所给的准则， 从被选中的初始状态出发建立一个可行解或部分解， 各个蚂蚁间通过信息素交换信息， 从而达到相互协作的目的。蚁群算法的思想已被应用到各个研究领域， 并取得了大量的研究成果， 而在VRPTW方面的研究则较少。

2 有时间窗的车辆路径问题

为简化问题的描述，需要在构建模型前做一些基本的假设和约束:

    (1) 假设物流运输车辆状况相同；

    (2) 单车运载力要大于单个客户需求量，且每条路线上的客户需求总量不大于单车最大运载力；

    (3) 配送中心能够满足所有客户需求，无缺货；

    (4) 车辆完成配送后直接返回配送中心；

(5) 每条路径长度不超过单车最大行程；

(6) 车辆要在时间窗内到达相应客户点，否则会产生惩罚成本；

 

向客户配送货物有时间限制，在此采用软时间窗的限制方法进行处理， 即对客户需求的货物在一定的时间范围内到达，若未能按时到达，则将对物流配送企业给予一定的罚金。则因不在时间窗内将产品送到客户点而产生的处罚成本用C5表示，公式如下所示：

    

其中：分别表示车辆早于和晚于时间窗将货物卸下而带来的损失成本。为车辆到达客户 j 的时刻，为车辆在客户 j 处等待的时间。

3 问题求解

蚁群算法（Ant Colony Algorithm）可以很好地解决 VRP，因为该算法在满足各需求点的时间窗约束的前提下采用动态信息策略， 以保证在每次搜索中每只蚂蚁都对搜索做出贡献， 

最快地找到最优解或满意解。简单来说，此算法是一种源于自然界中生物世界新的仿生类随机型、智能多主体搜索算法，它吸收了昆虫王国中蚂蚁的行为特性，通过其内在的搜索机制，在一系列困难的路径优化问题求解中取得了成效。所以本文打算通过 MATLAB 强大的计算功能编写蚁群算法程序来深入研究冷链物流路径优化问题。

基本蚁群算法的思路如下：

Begin

初始化：

Nc    0;（Nc为迭代次数）

对各边弧（i,j）;

        常数c;（较小的正数）    0;

     Ca    L;（ca为车辆的剩余载重量）

     Cb    N;（Cb为车辆的剩余行驶距离）

 读入其他输入参数;

 Loop:

     将初始点放入当前的解集中;

     While（不满足停机准则）do

     begin

     对每只蚂蚁k;

         按照剩余载重量，剩余行驶路径长和转移概率选择顶点j;

         将蚂蚁k从顶点i转移到顶点j;

         将顶点i放在当前的解集中;

     end

     当所有的城市都放在解集中，就记录蚂蚁的个数M    k;

     利用局部搜索机制来优化路径;

     然后计算每只蚂蚁的目标函数值;

     并计算当前的最好解;

     For k   1toM do

     begin

         对各边（i,j）,计算：;（增加的信息素）

     end

         对各边（i,j）,计算：;（轨迹更新）

         对各边（i,j）,置;

         ;

         若Nc<预定的迭代次数，则go to Loop;

     End 

 

1. 部分程序

2. % Author: 怡宝2号 博士猿工作室

3. % Use: 用蚁群算法求解有容量限制、时间窗限制的车辆路径问题；

4. % 坐标视自己的具体情况而定。

5. % Illustrate:输入变量（must）：

6. % coordinate：要求的相应点的坐标，第一行是点的横坐标，第二行是点的纵坐标

7. % demand（1*n），n表示工厂的个数；t表示各个工厂要求运送的货物的重量

8. % LimitW:每辆车限制的载重量

9. % Can—changed parameter： m：蚁群的规模

10. % MAXGEN：蚁群的最大迭代代数

11. %

12. % 输出： bestpop：最短路程对应的路径

13. % trace ：最短路程

14. % remark： 如有疑问请咨询qq：778961303

15. clc

16. clear all

17. close all

18. format compact

19.  

20. %蚁群参数初始化

21. Alpha = 1; %求解选择下一个城市的概率

22. Beta = 5; %求解选择下一个城市的概率

23. Rho = 0.75; %信息素的全局更新

24. Q = 200; %信息素增加强度系数

25. Elite = 1; %精英蚂蚁数量

26.  

27. m = 40; %每一代有40只蚂蚁

28. MAXGEN = 100; %最大迭代代数

29. Prab = 0.05; %伪随机选择概率

30.  

31. %读取初始数据，初始化成本函数的参数

32. [F,C,P,ZETA1,ZETA2,THETA,R,S,ELTAT,COSTP,V,BETA,OMEGA1,OMEGA2,coordinate,demand,ET,LT,ST,speed, LimitW] = initial();

33.  

34. %求各个客户点之间的距离

35. [Distance n] = CalculateD(coordinate); %n为客户数量，包括配送中心

36.  

37. Eta=1./Distance; %Eta为启发因子，离散模型设为距离的倒数

38. Tau=ones(n,n); %Tau为信息素矩阵，行：前一个城市的标号；列：后一个城市的标号。

39. Tabu=zeros(m,n+20); %存储并记录路径的生成

40.  

41. bestpop = zeros(MAXGEN,n+20); %每代最优的蚂蚁

42. trace = zeros(MAXGEN,1); %每代最小的成本

43.  

44. %迭代寻优开始开始

45. load = 0; %初始化载重

46. NC=1; %迭代计数器

47. while NC<=MAXGEN

48.  

49. Tabu(:,1)=1; %每只蚂蚁都是从仓库（及节点1）开始出发

50.  

51. %精英保留策略

52. start = 1;

53. if 2<=NC

54. start = Elite + 1;

55. end

56.  

57. for i=start:m

58. visited=Tabu(i,:);

59. visited=visited(visited>0);

60. to_visit=setdiff(1:n,visited); %在集合论中，to_visit = (1:n) - visited

61.  

62. actualST = zeros(n,1); %实际服务时间，初始化，一只蚂蚁初始化一次

63. actualST(1) = ET(1); %对初始点的服务时间，初始化

64. j=1;

65. while j<=n

66. if ~isempty(to_visit) %判断所有客户点是否送完

67. %计算接下来要参观的其他城市的概率

68. for k=1:length(to_visit)

69. [Tij actualST] = CalculateT( visited(end) , to_visit(k) ,actualST,Distance,ST,speed); %计算从客户i到达客户j的时间

70. VC = CalculateVC( visited(end) , to_visit , actualST , Distance , ST, speed, LT); %计算从客户i到下一个客户的潜在客户

71. x(k)=(Tau(visited(end),to_visit(k))^Alpha)*(Eta(visited(end),to_visit(k))^Beta)*...

72. 1/( abs(Tij-ET(to_visit(k))) + abs(Tij-LT(to_visit(k))) )*VC;

73. end

74.  

75. %伪随机选择，选择下一个城市

76. temp_pra=rand;

77. if temp_pra

78. Select=find(max(x));

79. else

80. x=x/(sum(x)); %用轮盘赌法选择下一个城市

81. xcum=cumsum(x);

82. Select=find(xcum>=rand);

83. end

84.  

85. %计算车的载重

86. if isempty(Select) %如果选不了下一个城市了，就回到1点

87. Select=1;

88. load=load+demand(Select); %select=1；t（select）=0

89. else

90. load=load+demand(to_visit(Select(1))); %select表示城市标号，to_visit(select)才表示城市

91. end

92.  

93. %判断载重是否超限，并对路径表修改

94. if load>W %判断车是否超载，超载就回到原地

95. Select=1;

96. j=j-1; %j表示参观了的城市，参观的城市-1

97. load=0; %车辆的载重归零

98. Tabu(i,length(visited)+1)=Select(1); %给车辆的路径信息赋值，及回到原点，要参观的客户赋值为1.

99. else

100. Tabu(i,length(visited)+1)=to_visit(Select(1));

101. end

102.  

103. end

104.  

105. %对访问过的客户，和待访问的客户初始化

106. visited=Tabu(i,:);

107. visited=visited(visited>0); %已经拜访过的客户

108. to_visit=setdiff(1:n,visited);

109. x=[];

110. if visited(end)~=1

111. Tabu(i,1:(length(visited)+1))=[visited,1];

112. end

113. j = j+1;

114. j;

115. end

116. %1只蚂蚁配送路线完成

117. load = 0;

118. end

119. %m只蚂蚁路线安排完成

120.  

121. %计算m只蚂蚁的个体适应度

122. L=zeros(m,1); %共有m只蚂蚁

123. for i=1:m

124. temp=Tabu(i,:);

125. route=temp(temp>0); %每只蚂蚁的路径

126. end

127.  

128. %精英保留策略

129. [ex index] = sort(L,'ascend');

130. index = index(1:Elite);

131. temp = Tabu(index,:);

132. tempL = L(index);

133. Tabu(1:Elite,:) = temp;

134. L(1:Elite) = tempL;

135.  

136. [mintrace index] = min(L); %最小的成本

137. temp = Tabu(index(1),:); %最小成本对应的蚂蚁

138. trace(NC) = mintrace; %保存每代的最小成本和最小蚂蚁

139. bestpop(NC,:) = temp;

140.  

141. %更新信息素

142. Delta_Tau=zeros(n,n);

143. for i=1:m

144. temp=Tabu(i,:);

145. route=temp(temp>0);

146. for j=1:(length(route)-1)

147. Delta_Tau(route(j),route(j+1))=Delta_Tau(route(j),route(j+1))+Q/L(i);

148. end

149. Delta_Tau(route(n),route(1))=Delta_Tau(route(n),route(1))+Q/L(i);

150. end

151. % %信息素更新

152. % Delta_Tau=zeros(n,n);

153. % for i=1:m

154. % temp=Tabu(i,:);

155. % route=temp(temp>0);

156. % for j=1:(length(route)-1)

157. % Delta_Tau(route(j),route(j+1))=Delta_Tau(route(j),route(j+1))+Q/L(i);

158. % end

159. % end

160. % Tau=(1-Rho).*Tau+Delta_Tau;

161.  

162. %路径清零，载荷清零

163. temp=zeros(m-Elite,n+20);

164. Tabu(Elite+1:m,:) = temp;

165. load=0;

166.  

167. disp(['共迭代',num2str(MAXGEN),'次,现在为：',num2str(NC)]);

168. % NC

169. NC = NC + 1;

170. end

171.  

172. %绘制寻优迭代图

173. figure()

174. plot(trace)

175. plot(trace,'--b',...

176. 'LineWidth',2);

177. grid off

178. xlabel('迭代次数数')

179. ylabel('成本')

180. title('成本变化','fontsize',16)

181.  

182. %显示路径

183. [mintrace index] = min(trace); %最小成本

184. route = bestpop(index,:); %最小成本的路径

185. route = route( route>0 );

186. p=num2str(route(1));

187. for i=2:length(route)

188. p=[p,'->',num2str(route(i))];

189. end

190. display(['求解的最优路径为：',num2str(p)]);

191. display(['1代表物流中心']);

192. disp(['最小的成本代价为：',num2str(min(trace))]);

193.  

194. %绘制最小成本的路径

195. figure();

196. DrawRoute(coordinate,route)

197.  

198.  

结果