优化算法之进化策略

clear all;clc;close all;
%进化策略解决旅行商问题
%{
日期：
20190912_ZD
遗传算法强调染色体的操作，进化策略强调个体级的行为变化，而进化规划则强
强调种群级别上的行为变化，现在学术界上将GA，ES，EP统称为进化算法EC
%}
t0 = clock;
N = 10;%初始种群规模
C = [1,2;70,90;80,60;10,100;800,200;800,100;90,80;200,600;230,4;500,90];%城市坐标
M = size(C,1);%城市个数
for i = 1:N
    X(i,:) = randperm(M);%初始种群
end
Inter = 5000;%迭代次数
BestFitness = -inf;%记录最大适应度
BestIndividual = zeros(1,M);%最优个体
BestFitnessInter = zeros(1,Inter);
MeanFitness = zeros(1,Inter);
D = zeros(M,M);
%计算各个城市之间的距离
for i = 1:M
    for j = 1:M
        D(i,j) = sqrt( sum((C(i,:) - C(j,:) ).^2));
    end
end
%进行迭代
for i = 1:Inter
    %随机生成新的种群
    NewX = zeros(100,N);%生成新的种群
    for Num = 1:100
        %通过初始种群繁殖生成新的种群（注重个体行为）
        pos1 =1 + fix( rand*N );
        pos2 = randperm(M);
        NewX(Num,:) = X(pos1,pos2);
    end
    %计算适应度
    Distance = zeros(Num,1);
    for k = 1:Num
        for kk = 1:N-1
            Distance(k) = Distance(k) + D(NewX(k,kk),NewX(k,kk+1));
        end
        Distance(k) = Distance(k) + D(NewX(k,1),NewX(k,end));
    end
    Fitness = 1 ./ Distance;
    %按照适应进行排名
    [SortFitness,Label] = sort(Fitness,'descend');
    LabelSelect = Label(1:N);
    %选择出N个新的初始种群
    X = NewX(LabelSelect,:);
    %比较最大适应度与原最大适应，并更新最大适应度
    if SortFitness(1) > BestFitness
        BestFitness = SortFitness(1);
        BestIndividual = NewX(Label(1),:);
    end
    BestFitnessInter(i) = BestFitness;
    MeanFitness(i) = mean(Fitness);
end
%绘制结果
time = etime(clock,t0);
disp('优化时间为')
disp(time)
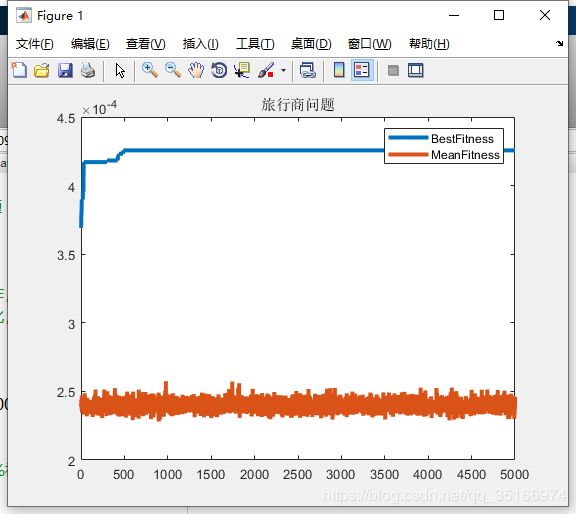
plot(BestFitnessInter,'LineWidth',3);
hold on
plot(MeanFitness,'LineWidth',3);
legend('BestFitness','MeanFitness')
title('旅行商问题')
disp('最短路径为：')
disp(BestIndividual)
disp('最短距离为：')
disp(1/BestFitness)
figure
BestIndividual = [BestIndividual,BestIndividual(1)];
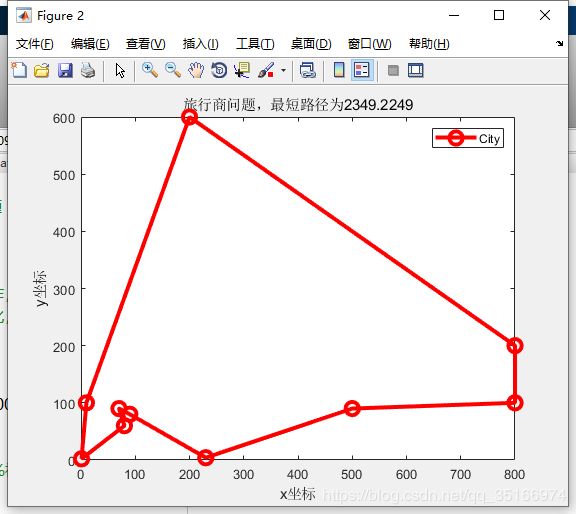
h = plot(C(BestIndividual,1),C(BestIndividual,2),'ro-');
set(h,'Linewidth',3,'MarkerSize',10)
title(['旅行商问题，最短路径为',num2str(1/BestFitness)]);
xlabel('x坐标');ylabel('y坐标')
legend('City')

运行结果：