凸优化笔记(1) —— 基本概念
凸优化笔记 —— 基本概念之凸集
- 1. 数学优化
- 基本概念
- 2.1 凸优化问题
- 2.2 线性函数与凸函数
- 2.3 凸集
- 仿射集。
- 2.3.2 凸集
- 2.3.3锥
- 三种集合的比较:
基本准备
本科没学过凸优化,想趁着还不是太忙,恶补下数学知识,终究是绕不过去的山。应该会不定时的更新凸优化、矩阵论的相关笔记吧,PRML、计算机视觉、概率图模型希望以后也能写一写笔记。
推荐的书籍:
英文版《Convex Optimization》
中文版(译本)《凸优化》(清华出版社)
推荐视频:
前中科大 凌青老师 (现在好像去了中山大学了)
视频在线地址:b站
网盘下载地址:http://pan.baidu.com/s/1slmHdTz 密码:9h61 (感谢,大智能时代’s Archiver上的分享)
纸质版书的话,英文版有点贵,中文版还好。PDF的话,上面我都给了链接了,英文版是作者的主页,可以免费下载最新版的PDF,中文版好像不是太新。视频的话,在线可以去b站上,下载的话也有网盘地址。不得不说b站真是个神奇的网站,很多斯坦福公开课我也是在上面看的,但是好像现在CS231N找不到。咳咳,扯远了~
另外,为了节省写博客的时间,书上的概念、公式会以截图的形式贴到博客上,重点在于自己的理解,和重点知识的归纳。书归正传,开始基本概念的笔记吧。
1. 数学优化
优化,即在可行解的范围内,找出最优解。用数学的形式可表达如下:
m i n i m i z e f 0 ( x ) s u b j e c t t o f i ( x ) ≤ b i , i = 1 , ⋯ , m minimize\: \: f_0\left ( x \right )\\ subject \:to\: \: f_i\left ( x \right )\leq b_i, \: \: i = 1,\cdots ,m minimizef0(x)subjecttofi(x)≤bi,i=1,⋯,m
,其中,向量x是问题的优化变量, f 0 f_0 f0是目标函数, f i f_i fi是约束函数。关于这个公式具体的定义如书上所言:
同样,也给出了最优解的概念。另外,目标函数和约束函数并不一定是单一的,都是可以存在多个的。
其实,对于数学优化问题,具体来点讲,比如在用做物理实验或者各种实验获得的数据,来拟合这些数据所表征的函数。假设,这些数据表征的是一个二次函数,即 y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c,在计算机上去拟合只能是去,先有个a、b、c的初始值,带入上述这个形式中,看与真实值的误差多大,然后向着是误差减小的地方来更新a、b、c的值,(有点类似于反向传播)。在这其中,误差就是目标函数,而限制条件,可能就是这些数据都是非负的,等等。优化问题的求解就是在一定的精度内,满足此一实例。就如上面这个问题,当误差在某一阈值之内的时候,求解就算完毕。
希尔伯特说过,问题可被描绘出来,就解决的了80%。而如果优化问题,能被描述出来还能被转换成凸优化问题,那么问题就解决了90%(凌青老师的话)
优化的分类
分类大概为:凸优化与非凸优化,线性优化与非线性优化,(针对目标函数)光滑与非光滑,连续与离散,多目标与单目标等。其中凸优化与非凸优化是界定优化问题较为准确地分界。粗略来讲,凸问题是较为简单的问题,非凸问题是较为难的问题。
基本概念
2.1 凸优化问题
什么是凸优化呢,简单来讲,就是上述数学优化问题中,目标函数是凸函数,约束问题属于凸集,或者是由若干凸函数组成的。那么,什么又是凸函数和凸集呢?
2.2 线性函数与凸函数
① 线性函数的定义:
f i ( α x + β y ) = α f i ( x ) + β f i ( x ) f_i\left ( \alpha x+\beta y \right )=\alpha f_i\left ( x \right )+\beta f_i\left ( x \right ) fi(αx+βy)=αfi(x)+βfi(x)
其中, α , β ∈ R \alpha,\: \beta \in R α,β∈R
② 凸函数的定义:
f i ( α x + β y ) ≤ α f i ( x ) + β f i ( x ) f_i\left ( \alpha x+\beta y \right )\leq \alpha f_i\left ( x \right )+\beta f_i\left ( x \right ) fi(αx+βy)≤αfi(x)+βfi(x)其中, α , β ∈ R + , 且 α + β = 1 \alpha,\: \beta \in R^+,且\alpha+\beta =1 α,β∈R+,且α+β=1
可以看出,线性函数属于凸函数,也就是说凸优化是比线性优化更为一般的问题。
2.3 凸集
仿射集。
第一种定义:
要注意,这个定义中需要是过集合内任意两点的直线,还在集合内。那,什么是直线呢?数学表达如下:

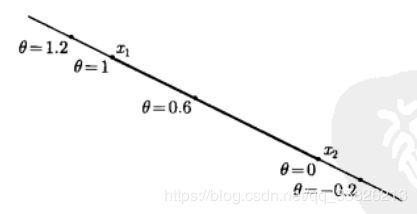
当把, Θ \Theta Θ设定在[0,1]之间时,直线就变成了了线段。下面这张图就很好地解释了这件事, Θ \Theta Θ的绝对值越来越大时,点就会离 Θ \Theta Θ为0的点越来越远,而 Θ \Theta Θ属于[0,1]时,也就只能包含 x 1 x_1 x1和 x 2 x_2 x2之间的点了。
仿射组合与第二种定义:

翻译过来就是,根据上面定义的仿射组合,如果对于仿射集C内任意个点的仿射组合都还属于C。这两种定义是等价的,证明省略,有兴趣可以看凌青老师视频第三集,证明也较为简单。
(1) 仿射集相关的子空间
另外,在仿射集的定义中,要求所有系数相加为1。那么是否有 α , β ∈ R \alpha,\: \beta \in R α,β∈R,而对于任意的点, α x 1 + β x 2 \alpha x_1+\beta x_2 αx1+βx2仍然属于C的情况呢?考虑一条穿过原点的直线,这样一个集合就是满足上述这样的性质的。
更普遍的来讲,不管在任意维度的空间内,一个集合的点只要统统减去集合内的值,那么这个集合一定经过空间内的原点。那么可以构造出一个与仿射集相关的子空间V:

同样V,也是一个仿射集,且 α v 1 + β v 2 \alpha v_1+\beta v_2 αv1+βv2仍然属于C。
(2) 线性方程的解

上述图片中证明了,仿射集必定是线性方程组的解集。结合上面的子空间的定义,可以清楚的看到,以C为解集的线性方程组,其中A·V必定等于0,即V是A的化零空间。
(3) 仿射包

其中,集合C若为仿射集,那么aff C就是其本本身,若C不是仿射集,那么aff C是包含C的最小的仿射集。
2.3.2 凸集
第一种定义:

从第一种定义的对比来看,仿射集限制要比凸集要大,满足线段在集合内要比满足直线在集合内要容易一些,这也是凸集包含仿射集的原因。
凸组合与第二种定义

在此不过多阐述,可以看一下较为明显的凸集和非凸集:

(1)凸包
与仿射包的定义相似,凸包的定义如下:

同样,如果C本身是凸集,那么conv C就是其本身,如果C不是凸集,那么conv C就是包含C的最小凸集。
2.3.3锥

其实,锥就是一系列射线,且射线的端点在原点处组合而成的集合,而本身又是凸集的锥就是凸锥。从上述定义的来说,构成的是一个扇面。如下图:
三种集合的比较:
仿射集: Θ 1 x 1 + ⋯ + Θ k x k , \Theta_1x_1+\cdots+ \Theta_kx_k, Θ1x1+⋯+Θkxk, \; \; 其中, Θ 1 + ⋯ + Θ k = 1 \Theta_1+\cdots +\Theta_k=1 Θ1+⋯+Θk=1
凸集: Θ 1 x 1 + ⋯ + Θ k x k , \Theta_1x_1+\cdots +\Theta_kx_k, Θ1x1+⋯+Θkxk, \; \; 其中, Θ 1 + ⋯ + Θ k = 1 , Θ 1 , ⋯ , Θ k ∈ [ 0 , 1 ] \Theta_1+\cdots +\Theta_k=1,\; \;\Theta_1,\cdots ,\Theta_k\in[0,1] Θ1+⋯+Θk=1,Θ1,⋯,Θk∈[0,1]
凸锥: Θ 1 x 1 + ⋯ + Θ k x k , \Theta_1x_1+\cdots +\Theta_kx_k, Θ1x1+⋯+Θkxk, \; \; 其中, Θ 1 , ⋯ , Θ k ∈ R + \Theta_1,\cdots ,\Theta_k\in R^+ Θ1,⋯,Θk∈R+