AB实验样本量确定

在数据分析过程中， 一个完整的闭环是从数据中得到洞察，根据洞察得到某种假设，通过实验检验这一假设。

AB实验实际上是在做一个假设检验，可以参考上一篇笔记【概率论】- (2)假设检验。在查资料的过程中，查到AB实验主要有两种检验方式（不同的样本量，不同的检验方式）——

• Z检验，即检验实验组与对照组服从分布的均值是否相等
• 卡方检验，即检验实验组是否服从理论分布（将对照组看成理论分布）

这里以Z检验为例，介绍如何确定AB实验中实验组与对照组的样本量，提供相应的代码，卡方检验原理相似。

1. 统计功效与关键概念

在假设检验中有以下两类错误——

• 弃真：原假设为真，而我们拒绝原假设，这种错误称为一型错误
• 取伪：原假设为假，而我们接受原假设，这种错误称为二型错误

在教科书中一般只限定显著性水平为 $\alpha$，即只考虑一型错误的概率，而不考虑二型错误。但在实际应用中（如AB实验），二型错误也必须限定在较低的范围内。如下例子，这种情况下即使 $\alpha$ 足够小，实验结果仍不够具有说服性。

假设实验的显著性水平 $\alpha =0.01$，二型错误概率 $\beta =0.5$，这意味着——

• 若原假设为真，我们判断出错（即拒绝）的概率为1%；
• 若原假设为假，我们判断出错（即接受）的概率为50%。

上面说的考虑二型错误，更常见的是考虑统计功效Statistical Power。

统计功效是指当原假设为假，拒绝原假设的概率。因此有 $power=1-\beta$。

通过求解统计功效，即可得到统计功效与 $\alpha 、n$ 的关系式。反过来，知道 $\alpha 、power$ 后就可以求出所需的样本量。

2. Z检验样本量确定

2.1 统计功效公式推导

• 原假设与备择假设如下：

$$\begin{gathered} H_0:{\mu }_A={\mu }_B \\ {H}_1:{\mu }_A\ne {\mu }_B\text{\hspace{1em}(1)} \end{gathered}$$

• 令 $\delta ={\mu }_A-{\mu }_B$，按照二型错误的概念，假设 ${\sigma }_A={\sigma }_B=\sigma$， 有

$$\begin{array}{rl}\beta & =P(接受H_0|H_0为假)\\ & =P(-z_{\alpha /2}\le \frac{{\bar{x}}_A-{\bar{x}}_B}{\sigma /\sqrt{n_A+n_B}}\le z_{\alpha /2}|\delta \ne 0)\\ & =P(-z_{\alpha /2}-\frac{\delta }{\sigma /\sqrt{n_A+n_B}}\le \frac{({\bar{x}}_A-{\bar{x}}_B)-\delta }{\sigma /\sqrt{n_A+n_B}}\le z_{\alpha /2}-\frac{\delta }{\sigma /\sqrt{n_A+n_B}})\\ & =\varphi (z_{\alpha /2}-\frac{\delta }{\sigma /\sqrt{n_A+n_B}}))-\varphi (-z_{\alpha /2}-\frac{\delta }{\sigma /\sqrt{n_A+n_B}}))\end{array}\text{\hspace{1em}(2)}$$

注意，由于 $H_0$ 为假，即 ${\mu }_A\ne {\mu }_B$，$\frac{{\bar{X}}_A-{\bar{X}}_B}{\sigma /\sqrt{n_A+n_B}}$ 不服从正态分布，所以需要转化为$\frac{({\bar{X}}_A-{\bar{X}}_B)-\delta }{\sigma /\sqrt{n_A+n_B}}$ 才服从标准正态分布。

• 令 $z=\frac{{\mu }_A-{\mu }_B}{\sigma /\sqrt{n_A+n_B}}$，由统计功效与二型错误的关系，有

$$\begin{array}{rl}power=1-\beta & =1-\varphi (z_{\alpha /2}-z)+\varphi (-z_{\alpha /2}-z)\\ & =\varphi (-z_{\alpha /2}+z)+\varphi (-z_{\alpha /2}-z)\end{array}\text{\hspace{1em}(3)}$$

• 这样就得到了统计功效power的表达式。

2.2 样本量计算公式

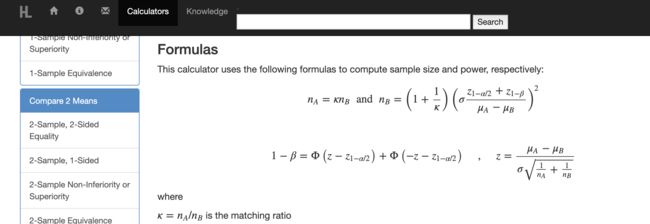
上述推导出了统计功效的计算公式，当然计算样本量已经有很多工具，比如Z检验计算样本量工具，这个工具中也提供了计算公式，与上面推导出的类似，注意区别在于这个工具的$z_{1-\alpha /2}$ 是下分位点，上述推导是上分位点。

从这个网站的公式中也可以看到样本量的计算公式。

2.3 求解样本量

python中提供了假设检验的函数（R中也有类似的函数，参考pwr功效分析R包），Z检验的函数定义如下，使用的时候提供参数，留一个未知参数（None），返回值为未知参数的计算结果，看后面的具体例子。

from statsmodels.stats.power import NormalIndPower
NormalIndPower().solve_power(
    effect_size=None,
    nobs1=None,
    alpha=None,
    power=None,
    ratio=1.0,
    alternative='two-sided',
)

第一个参数effect_size表示效应量，代表不同处理下总体差异的大小（即判断有没有差别，还要判断差多少）。在Z检验中确定样本量可以使用 $\frac{|{\mu }_A-{\mu }_B|}{\sigma }$ 近似效应量。

假设原方案的留存率为0.40，新方案的留存率预计为0.45，方差为1，则求解样本量如下：

• 使用python函数计算，得到第一组为6280人，第二组与第一组相等（ratio=1）
  

• 按照公式计算，两个Z值查表得到，代入公式，求得样本量均为6280，与上面一致
  

• 使用Z检验计算样本量工具，结果为6267，与上述计算结果差异较小，猜测为效应量公式不同。使用另一个Z检验计算样本量工具计算结果则相同，为6280
  

3. 卡方检验样本量确定

卡方检验的推导思路应该与Z检验大致相同，我没有去尝试，这里直接用python函数求解，并与工具对比。

3.1 求解样本量

python提供的卡方检验函数如下，使用方法与Z检验的函数相同。

from statsmodels.stats.power import GofChisquarePower
GofChisquarePower().solve_power(
    effect_size=None,
    nobs=None,
    alpha=None,
    power=None,
    n_bins=2,
)

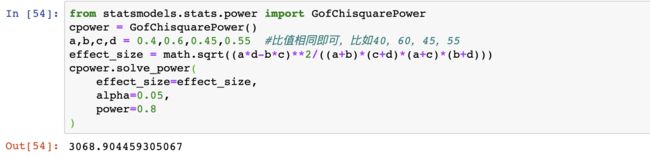
卡方检验中，四格表的效应量计算公式如下（百度百科-效应量）:
$$\varphi =\sqrt{\frac{{\chi }^2}{n}}=\sqrt{\frac{n(ad-bc{)}^2/[(a+b)(c+d)(a+c)(b+d)]}{n}}=\sqrt{(ad-bc{)}^2/[(a+b)(c+d)(a+c)(b+d)]}$$
假设原方案的留存率为0.40，新方案的留存率预计为0.45，方差为1，则求解样本量如下：

• 使用python函数计算，样本量为3068，则每组1534
  

• 使用卡方检验计算样本量工具结果如下，每组样本量为1514，与上述函数结果有较小差异

• 使用另一个卡方检验计算样本量工具结果如下，每组样本量也为1514
  
  两个工具均为1514，猜测与我们自己计算的结果不同原因为效应量计算方式不同。

4. 简要总结

因为没有实际进行过AB实验，不太清楚实际应用中使用的是哪种方式。个人认为卡方检验更为方便实用，一方面是样本量更少，实验成本更低，另一方面需要提供的参数也更少（不需要提供方差）。

以上是我对于AB实验样本量计算的一些思考，如有错误，请大佬指正～

Reference

1. 《浙江大学概率论与数理统计第四版》

2. 略谈假设检验第二类错误的概率

3. Z检验计算样本量工具

4. 另一个Z检验计算样本量工具

5. pwr功效分析R包

6. 卡方检验计算样本量工具

7. 另一个卡方检验计算样本量工具