EKFmonocularSLAM论文阅读笔记(二)
三、单点RANSAC扩展卡尔曼滤波器
1.状态向量定义
在第 k k k步中的状态向量由一组摄像机参数 x C k W x_{C_k}^{W} xCkW和地图参数 y W y^W yW组成。尽管在将它们引用到当前相机帧 C k C^k Ck方面有一些优点,所有这些通常被称为静态参考帧 W W W:
![]()
估计的地标 y W y^W yW由n个点特征 y i W = ( y 1 W , y 2 W , . . . . . . , y n W ) T y_{i}^{W}=(y_{1}^{W},y_{2}^{W},......,y_{n}^{W})^{T} yiW=(y1W,y2W,......,ynW)T组成;如果投影方程变得足够线性时,点特征将在逆深度坐标 y i , I D W = ( X i W , Y i W , Z i W , θ i W , ϕ i W , ρ i ) T y_{i,ID}^W=(X_{i}^W,Y_{i}^W,Z_{i}^W,{\theta}_{i}^W,{\phi}_{i}^W,{\rho}_i)^T yi,IDW=(XiW,YiW,ZiW,θiW,ϕiW,ρi)T中被参数化并被转换为欧几里得参数 y i , E W = ( X i W , Y i W , Z i W ) T y_{i,E}^W=(X_{i}^W,Y_{i}^W,Z_{i}^W)^T yi,EW=(XiW,YiW,ZiW)T。 逆深度参数会存储特征初始化 ( X i W , Y i W , Z i W ) T (X_{i}^W,Y_{i}^W,Z_{i}^W)^T (XiW,YiW,ZiW)T时的3D相机位置的六个参数,指向特征的单位射线及其沿射线 ρ i \rho_i ρi的逆深度的偏航角 – 俯仰角对 θ i W , ϕ i W {\theta}_{i}^W,{\phi}_{i}^W θiW,ϕiW。
2.动态模型
应用于相机的动态模型取决于可用的信息。对于单眼序列纯视觉估计的情况,恒速模型对于平滑的手持运动是足够的。 摄像机状态由位置 r C k W r_{C_k}^W rCkW,方位 q C k W q_{C_k}^W qCkW以及线性和角速度 v W v^W vW和 ω C k \omega^{C_k} ωCk形成:

等速模型 f v f_v fv等式如下:
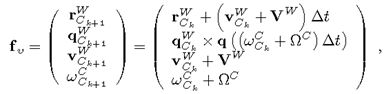
其中, V W V^W VW和 Ω C \Omega^C ΩC是来自加速冲量的零均值高斯分布速度噪声。
当除单眼序列之外的其他感觉信息可用时,应该将其作为输入结合到动态模型中。 本文分析了单目视觉加轮测距的组合。 在这种情况下,相机状态只需要包含位置和方向 X C k W X_{C_k}^W XCkW。
3.测量模型
在本文实验中使用的测量模型是一个针孔摄像机模型加上两个参数的径向畸变,假设相机已经提前校准。 首先将状态向量中的逆深度和欧几里得点转换为相机参考帧:
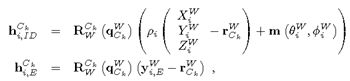
其中, R W C k R_{W}^{C_k} RWCk表示从状态四元数计算的旋转矩阵, m m m是将方位角-仰角转换为单位矢量的函数。 然后使用标准针孔模型投影相机框架中的点:

这里 f f f代表相机的焦距, ( u 0 ; v 0 ) (u0; v0) (u0;v0)是图像中心坐标。 成像点最终使用下面的两个参数 k 1 , k 2 k_1,k_2 k1,k2模型进行变换,导致失真测量 h d = ( u d , v d ) h_d =(u_d,v_d) hd=(ud,vd)。
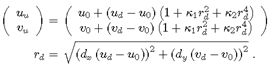
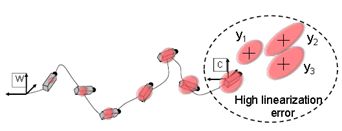
图(a)世界参考EKF估计。 当摄像机远离世界参考点并且不会重新访问已知位置时,摄像机和新初始化特征 y i y_i yi的不确定性都会增加。 广泛的不确定性区域将产生高线性化误差和滤除不一致性。
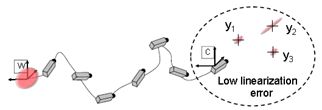
图(b)以相机为中心的EKF估计。 相机的位置不确定性接近于零,因为参考始终与其相连。 其周围特征的不确定性也会保持较低,因此测量模型线性化误差在整个估计中将保持较小。
4.以摄像头为中心的估计
众所周知,通常的EKF SLAM公式以世界坐标系作为参考坐标系,仅适用于传感器周围的局部估计。但是,随着传感器远离世界参考点,并且如果执行纯探索性移动,估计的不确定性将会一直增加。 最终它会达到一个点,该点会因为大的线性化误差导致不一致和滤波器分歧。
那么,使用以相机为中心进行视觉EKF估计,同时将所有几何参数引用到连接到相机的参考框架内,就会使得传感器局部的不确定性始终保持较低,而且大大降低了与测量模型相关的线性化误差。
现在详细介绍关于以世界为中心的视觉SLAM的修改。 首先,状态矢量由世界坐标系 x W C k x_{W}^{C_k} xWCk的位置和估计特征的映射 y C k y^{C_k} yCk组成,二者均在当前相机参考帧中表示:
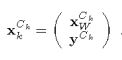
相对于当前相机 x W C k x_{W}^{C_k} xWCk的世界参考的位置,用其位置 r W C k r_W^{C_k} rWCk和四元数定向 q W C k q_{W}^{C_k} qWCk进行编码。 当里程计信息不可用并且假定是等速模型时,速度也应包括在状态 x k C k x_k^{C_k} xkCk中。
对于时间 k k k的预测步骤,在时间 k − 1 k-1 k−1将世界参考系和特征映射保留在参考系中,并且添加代表 k − 1 k-1 k−1和 k k k之间的传感器运动的新特征:
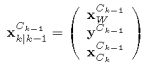
预测的相机运动用位置和方向表示,用四元数表示:
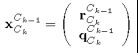
单点RANSAC EKF算法适用于较小的变化。 该系统的动态模型被应用在相对于包含在 x C k C k − 1 x_{C_k}^{C_{k-1}} xCkCk−1中的前一帧的运动中,或者恒定速度模型或轮距测量输入。在算法结束时,在第二次更新后,应用刚性变换将参考帧从前一个摄像机更改为当前摄像机,更新世界参考位置:
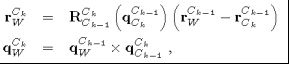
并且表示从前一帧到当前帧 x C k C k − 1 x_{C_k}^{C_{k-1}} xCkCk−1的运动的参数被从该状态边缘化出来。 逆深度和欧几里得地图特征也受这个组合步骤的影响:

协方差使用该组合函数 J J J的雅可比矩阵进行更新。