数据挖掘十大算法（二）：K-Means、二分K-均值 python和sklearn实现

早在刚接触数据挖掘算法时就已经看过，以及使用过简单的K-均值算法来做聚类，现在为了进一步的掌握该知识，通过机器学习实战又看了一遍，由于相对于其它算法较简单，所以看的也比较快，同时也学习了一下更为强大的二分K-均值算法，该算法建立在K-Means算法上，但难度不大，理论知识也很好理解，所以这里对两者的思路都记录一下。本篇文章主要内容（K-Means原理、二分K-Means原理、基础代码实现、sklearn实现）等。

K-Means原理：

    聚类是一种无监督的学习，它将相似的对象归到同一个簇中。有点像全自动分类，聚类方法几乎可以应用于所有对象，簇内的对象越相似，聚类的效果越好。K-均值（K-Means）属于聚类算法，之所以称为K-均值是因为它可以发现k个不同的簇，且每个簇的中心采用簇中所含值得均值计算而成。

实现聚类的思想：

1. 随机选择K个中心值
2. 根据样本数据各点与中心点的距离来进行归簇
3. 通过整个簇的均值，重置每个簇的中心值
4. 重复2、3，直至达到最大的迭代次数（例如：我这里的条件设置为本次与上次的平方误差相等）

看了这个步骤，感觉不会算法得人，都应该有了大概的思路。下面通过作者的代码来演示具体的操作：

代码：

样例数据（来自第十章）：

from numpy import *
import matplotlib.pyplot as plt

# 加载本地数据
def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float,curLine)) # 映射所有数据为浮点数
        dataMat.append(fltLine)
    return dataMat

# 欧式距离计算
def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2))) # 格式相同的两个向量做运算

# 中心点生成 随机生成最小到最大值之间的值
def randCent(dataSet, k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n))) # 创建中心点，由于需要与数据向量做运算，所以每个中心点与数据得格式应该一致（特征列）
    for j in range(n):  # 循环所有特征列，获得每个中心点该列的随机值
        minJ = min(dataSet[:,j])
        rangeJ = float(max(dataSet[:,j]) - minJ)
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1)) # 获得每列的随机值 一列一列生成
    return centroids

# 返回 中心点矩阵和聚类信息
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2))) # 创建一个矩阵用于记录该样本 （所属中心点 与该点距离）
    centroids = createCent(dataSet, k)
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False  # 如果没有点更新则为退出
        for i in range(m):
            minDist = inf; minIndex = -1
            for j in range(k):  # 每个样本点需要与 所有 的中心点作比较
                distJI = distMeas(centroids[j,:],dataSet[i,:])  # 距离计算
                if distJI < minDist:
                    minDist = distJI; minIndex = j
            if clusterAssment[i,0] != minIndex: # 若记录矩阵的i样本的所属中心点更新，则为True，while下次继续循环更新
                clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2   # 记录该点的两个信息
        # print(centroids)
        for cent in range(k): # 重新计算中心点
            # print(dataSet[nonzero(clusterAssment[:,0] == cent)[0]]) # nonzero返回True样本的下标
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]] # 得到属于该中心点的所有样本数据
            centroids[cent,:] = mean(ptsInClust, axis=0) # 求每列的均值替换原来的中心点
    return centroids, clusterAssment

datMat = mat(loadDataSet('testSet.txt'))
myCentroids,clustAssing = kMeans(datMat,4)
print(myCentroids)
print(clustAssing)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(myCentroids[:,0].flatten().A[0],myCentroids[:,1].flatten().A[0],color='r',s=60)
ax.scatter(datMat[:,0].flatten().A[0],datMat[:,1].flatten().A[0])
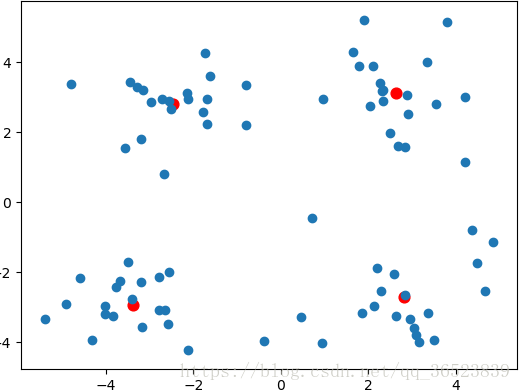
plt.show()

中心点：

每个点的所属簇、及平方和误差：

K-Means算法很简单，实现起来也不困难，这是它的优势，但有时你可能会发现K-均值收敛，但聚类效果并不是很好，这是因为K-均值收敛到了局部最小值，而非全局最小值（局部最小值表示结果还可以，但还可以更好，全局最小值表示结果可能是最好的了）。

由此我们需要使用后处理来提高聚类性能，一种度量聚类效果的指标是SSE（误差平方和），就是上面clusterAssment的第一列之和。SSE越小表示越接近质心点，由于取了平方，所以更重视距离远的点。增加簇可以减少SSE，但这可能不符合要求，另一种方法是将具有较大SSE的簇进行二分，具体实现时可以将最大簇包含的点过滤出来并在这些点上运用K-均值算法，K设为2。

基于划分簇的思想下面介绍二分K-均值

二分K-均值：

    首先将所有点作为一个簇，然后将该簇一分为二。之后选择一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。而划分就是上面提到的K-均值的思想了，利用上面的函数k设为2来划分。通过不断重复的操作，直到达到需要的簇数量。

代码：

样例数据：

# 二分均值聚类    SSE误差平方和    nonzero判断非0或给定条件，返回两个数组，[0]为True的下标组
def biKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))  # 保存数据点的信息（所属类、误差）
    centroid0 = mean(dataSet, axis=0).tolist()[0]   # 根据数据集均值获得第一个簇中心点
    centList =[centroid0] # 创建一个带有质心的 [列表]，因为后面还会添加至k个质心
    for j in range(m):
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2     # 求得dataSet点与质心点的SSE
    while (len(centList) < k):
        lowestSSE = inf
        for i in range(len(centList)):
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:] # 与上面kmeans一样获得属于该质心点的所有样本数据
            # 二分类
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)  # 返回中心点信息、该数据集聚类信息
            sseSplit = sum(splitClustAss[:,1])  # 这是划分数据的SSE    加上未划分的 作为本次划分的总误差
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])   # 这是未划分的数据集的SSE
            print("划分SSE, and 未划分SSE: ",sseSplit,sseNotSplit)
            if (sseSplit + sseNotSplit) < lowestSSE:    # 将划分与未划分的SSE求和与最小SSE相比较 确定是否划分
                bestCentToSplit = i         # 得出当前最适合做划分的中心点
                bestNewCents = centroidMat  # 划分后的两个新中心点
                bestClustAss = splitClustAss.copy() # 划分点的聚类信息
                lowestSSE = sseSplit + sseNotSplit
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList)   # 由于是二分，所有只有0，1两个簇编号，将属于1的所属信息转为下一个中心点
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit # 将属于0的所属信息替换用来聚类的中心点
        print('本次最适合划分的质心点: ',bestCentToSplit)
        print('被划分数据数量: ', len(bestClustAss))
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0] # 与上面两条替换信息相类似，这里是替换中心点信息，上面是替换数据点所属信息
        centList.append(bestNewCents[1,:].tolist()[0])
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:] = bestClustAss # 替换部分用来聚类的数据的所属中心点与误差平方和 为新的数据
    return mat(centList), clusterAssment

datMat3 = mat(loadDataSet('testSet2.txt'))
centList,myNewAssments = biKmeans(datMat3,3)
print(centList)
print(myNewAssments)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(centList[:,0].flatten().A[0],centList[:,1].flatten().A[0],color='r',s=60)
ax.scatter(datMat3[:,0].flatten().A[0],datMat3[:,1].flatten().A[0])
plt.show()

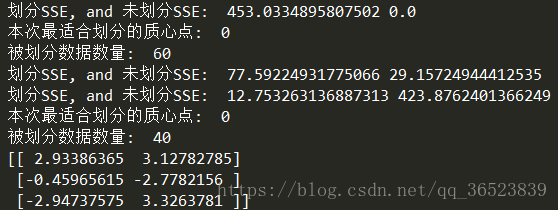
中心值：

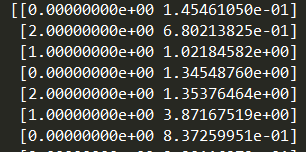
每个点的所属簇、及SSE值：

大部分的解释都在代码上，这里就不再累述了。二分K-均值相比于K-均值效果更好，克服了K-Means算法收敛于局部最小值得问题。

sklearn实现：

由于篇幅问题，这里简单说一下。通过sklearn的cluster可以使用KMeans算法，或者使用另一种方法Mini Batch K-Means。

Mini Batch K-Means算法是K-Means算法的变种，采用小批量的数据子集减小计算时间，同时仍试图优化目标函数，这里所谓的小批量是指每次训练算法时所随机抽取的数据子集，采用这些随机产生的子集进行训练算法，大大减小了计算时间，与其他算法相比，减少了k-均值的收敛时间，小批量k-均值产生的结果，一般只略差于标准算法。

官方文档的连接：http://scikit-learn.org/stable/modules/clustering.html#mini-batch-kmeans

可以参考的博客：

https://blog.csdn.net/sinat_26917383/article/details/70240628    参数含义

https://blog.csdn.net/gamer_gyt/article/details/51244850

 

当然如果可以的话，最好使用官方的文档进行深入的学习。

参考书籍：《机器学习实战》