编译原理习题上（3，4，5章）

词法分析

3.3.5

包含5个元音的所有小写字母串，这些串中的元音按顺序出现

vowel -> other* a (other|a)* e (other|e)* i (other|i)* o (other|o)* u (other|u)*
other -> [bcdfghjklmnpqrstvwxyz]

3.4.1

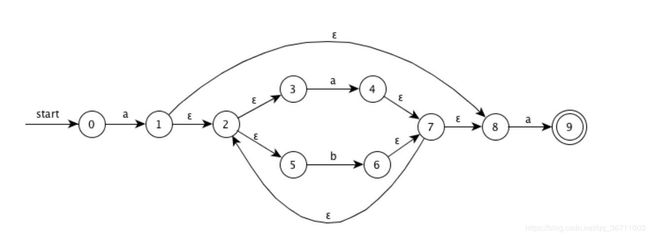
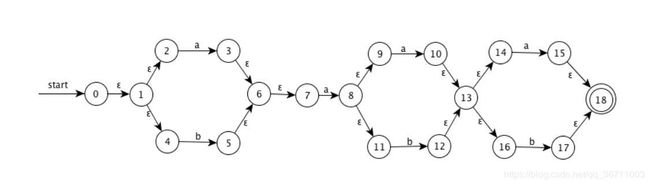
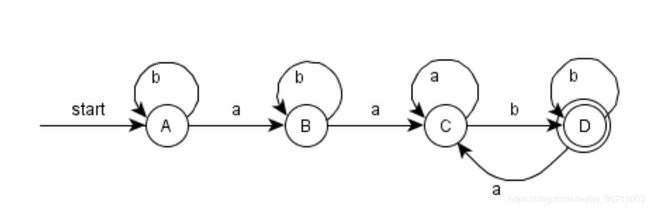
给出识别下列各个正则表达式所描述的语言状态转换图。

1. a(a|b)*a

NFA:

DFA:

NFA	DFA	a	b
{0}	A	B
{1,2,3,5,8}	A	B	C
{2,3,4,5,7,8,9}	C	C	D
{2,3,5,6,7,8}	D	C	D

最少状态的 DFA(状态转换图):合并不可区分的状态 B 和 D

2. ((ε|a)b*)*

3. (a|b)*a(a|b)(a|b)
   NFA:
   

DFA:

NFA	DFA	a	b
{0,1,2,4,7}	A	B	C
{1,2,3,4,6,7,8,9,11}	B	D	E
{1,2,4,5,6,7}	C	B	C
{1,2,4,5,6,7,12,13,14,16}	E	H	I
{1,2,3,4,6,7,8,9,10,11,13,14,15,16,18}	F	F	G
{1,2,4,5,6,7,12,13,14,16,17,18}	G	H	I
{1,2,3,4,6,7,8,9,11,15,18}	H	D	E
{1,2,4,5,6,7,17,18}	I	B	C

最少状态的 DFA(状态转换图):合并不可区分的状态 A 和 C

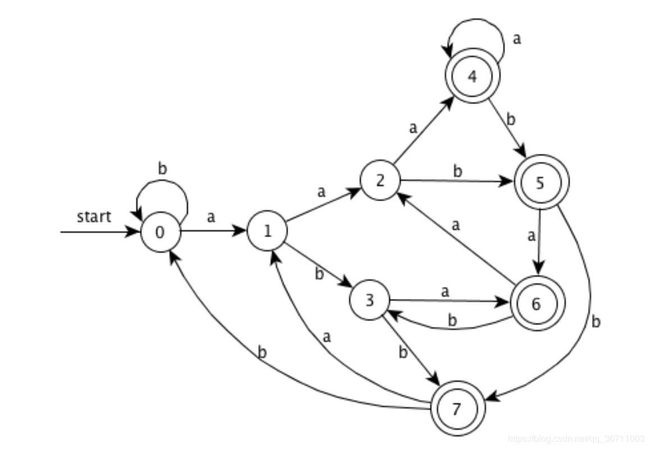
4. a*ba*ba*ba*

3.7.1

将下图的NFA转换为DFA
1.

NFA转换表

state	a	b	ε
0	{1}	∅	{3}
1	∅	{2}	{0}
2	∅	{3}	{1}
3	{0}	∅	{2}

state	a	b
0	{0,1,2,3}	{0,1,2,3}
1	{0,1,2,3}	{0,1,2,3}
2	{0,1,2,3}	{0,1,2,3}
3	{0,1,2,3}	{0,1,2,3}

NFA	DFA	a	b
{0,1,2,3}	A	A	A

state	a	b
0	{0,1}	{0}
1	{1,2}	{1}
2	{0,1,2}	{0,2,3}
3	∅	∅

NFA	DFA	a	b
{0}	A	B	A
{0,1}	B	C	B
{0,1,2}	C	C	D
{0,1,2,3}	D	C	D

语法分析

4.4.2

有没有可能通过某种方法修改下面文法，构造出一个与该练习中的语言（运算分量为 a 的后缀表达式）对应的预测分析器？

S -> SS+ | SS* | a

1. 提取左公共因子

S -> SSA | a
A -> + | *

2. 消除左递归

S -> aB
B -> SAB | ε
A -> + | *

3. 构造预测分析表

• First(S) = {a},First(B) = {a, ε},First(A) = {+,*}
• Follow(S) = {+,*,$},Follow(B) = {+,*,$},Follow(A) = {a}

非终结符号	输入符号
	+	*	a	$
S			S -> aB
A	A -> +	A -> *
B	B -> ε	B -> ε	B -> SAB	B -> ε

4.4.1

对下面的文法构造预测分析表

    bexpr -> bexpr or bterm | bterm
    bterm -> bterm and bfactor | bfactor
    bfactor -> not bfactor | ( bexpr ) | true | false

1. 无左公共因子
2. 消除左递归

	bexpr -> bterm A
	A -> or bterm A | ε
	bterm -> bfactor B
	B -> and bfactor B | ε
	bfactor -> not bfactor | ( bexpr ) | true | false

3. 预测分析表

first(bexpr) =first(bterm)  = first(bfactor)=  {not,(,true,false};
first(A) = {or,ε};
first(B) = {and,ε};
follow(bexpr) = follow(A) = {),$};
follow(bterm) = follow(B) = {or,),$};
follow(bfactor) = {and,or,),$};

非终结符号	输入符号
	and	or	not	(	)	true	false	$
bexpr			bexpr -> bterm A	bexpr -> bterm A		bexpr -> bterm A	bexpr -> bterm A
A		A -> or bterm A			A -> ε			A -> ε
bterm			bterm -> bfactor B	bterm -> bfactor B		bterm -> bfactor B	bterm -> bfactor B
B		B -> and bfactor B | ε			B -> ε			B -> ε
bfactor			bfactor -> not bfactor	bfactor -> (bexpr)		bfactor -> true	bfactor -> false

4.5.2

对于文法 S -> S S + | S S * | a 和下面各个最右句型,指出最右句型的句柄。

1. SSS+a*+
   SS+
2. SS+a*a+
   SS+
3. aaa*a++
   a

4.5.3

对于下面的输入符号串和文法，说明相应的自底向上语法分析过程。
练习 文法 S -> S S + | S S * | a ,串 aaa*a++

栈	输入	句柄	动作
$	aaa*a++$		移入
$a	aa*a++$	a	归约:S -> a
$S	aa*a++$		移入
$Sa	a*a++$	a	归约：S -> a
$SS	a*a++$		移入
$SSa	*a++$	a	归约：S -> a
$SSS	*a++$		移入
$SSS*	a++$	SS*	归约：S -> SS*
$SS	a++$		移入
$SSa	++$	a	归约：S -> a
$SSS	++$		移入
$SSS+	+$	SS+	归约：S -> SS+
$SS	+$		移入
$SS+	$	SS+	归约：S -> SS+
$S	$		接受

4.6.2

为下面的文法构造SLR项集。计算这些项集的GOTO函数。给出这个函数的语法分析表。这个文法是SLR文法吗？

S->SS+|SS*|a

1. 提取左公因子和消除左递归后的增广文法

	S' -> S
    S -> a B
    B -> a B A B
    B -> ε
    A -> +
    A -> *

2. LR(0)项目集

3. 语义分析表

	FOLLOW(S) = [$]
    FOLLOW(A) = [a,+,*, $]
    FOLLOW(B) = [+, * ,$]

状态	ACTION				GOTO
	a	+	*	$	S	A	B
0	s2				1
1				acc
2	s4	r3	r3	r3			3
3				r1
4	s4	r3	r3	r3			5
5		s7	s8			6
6	s4	r3	r3	r3			9
7	r4	r4	r4	r4
8	r5	r5	r5	r5
9		r2	r2	r2

无冲突，这显然是一个 SLR 文法

4. 利用语法分析表，给出处理输入aa*a+时的各个动作。

	栈	符号	输入	动作
(1)	0		aa*a+$	移入
(2)	02	a	a*a+$	移入
(3)	024	aa	*a+$	归约：B -> ε
(4)	0245	aaB	*a+$	移入
(5)	02458	aaB*	a+$	归约：A -> *
(6)	02456	aaBA	a+$	移入
(7)	024564	aaBAa	+$	归约：B -> ε
(8)	0245645	aaBAaB	+$	移入
(9)	02456457	aaBAaB+	$	归约：A -> +
(10)	02456456	aaBAaBA	$	归约：B -> ε
(11)	024564569	aaBAaBAB	$	归约：B -> aBAB
(12)	024569	aaBAB	$	归约：B -> aBAB
(13)	023	aB	$	归约： S -> aB
(14)	0	S	$	接受

4.6.6

说明下面的文法

	S->SA|A
    A->a

是SLR(1)的，但不是LL(1)的

左递归文法和二义性的文法都不可能是LL(1)文法。

1. 无左公共因子，消除左递归

	S' -> S
	S -> AB
	B -> AB
	B ->  ε
	A->a

2. 预测分析表

	first(S) = first(A)= {a};
	first(B) = {a, ε};
	follow(S) = follow(B) = {$};
	follow(A)= {a,$};

状态	ACTION		GOTO
	a	$	S	A	B
0	s3		s1	s2
1		acc
2	s3	r3		s5	s4
3	r4	r4
4		r1
5	s3	r3		s5	s6
6		r2

该文法生成的语法分析表是没有冲突的

4.7.1

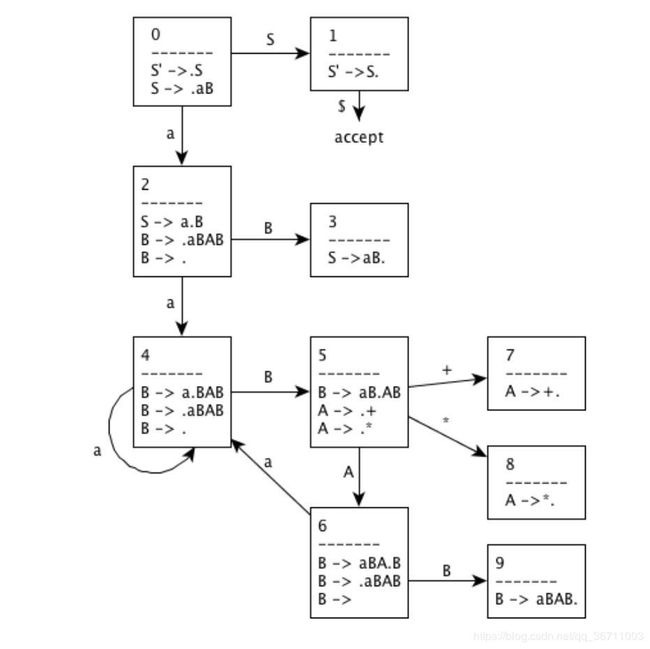
为练习 4.2.1 的文法 S -> S S + | S S * | a 构造

1. 规范 LR 项集族
2. LALR 项集族

4.7.5

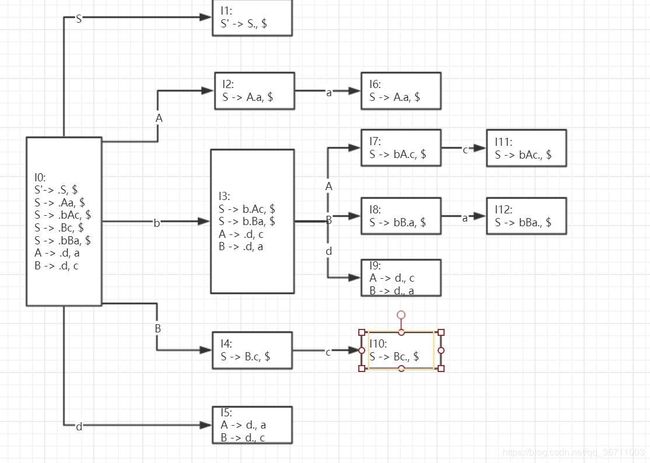
说明下面的文法

    S -> A a | b A c | B c | b B a
    A -> d
    B -> d

是 LR(1) 的，但不是 LALR(1) 的

1. 构造该文法的增广文法如下：

	S' -> S
	S -> Aa
	S -> bAc
	S -> Bc
	S -> bBa
	A -> d
	B -> d

2. 构造该文法的LR(1)项目集如下：

3. 构造LR(1)分析表

GOTO(I0，S)=I1  GOTO(I0，A)=I2   GOTO(I0，b)=I3   GOTO(I0，B)=I4  GOTO(I0，d)=I5 
GOTO(I1,$)=acc  
GOTO(I2，a)=I6   
GOTO(I3，A)=I7  GOTO(I3，B)=I8 GOTO(I3，d)=I9  
GOTO(I4，c)=I10  
GOTO(I7，c)=I11  
GOTO(I8，a)=I12

状态	ACTION					GOTO
	a	b	c	d	$	S	A	B
0		s3		s5		1	2	4
1					acc
2	s6
3				s9			7	8
4			s10
5	r5		r6
6					r1
7			s11
8	s12
9	r6		r5
10					r3
11					r2
12					r4

可见该分析表中不存在二义性的条目，故该文法是LR(1)文法

4. 合并I5和I9项目集，构造LALR分析表

状态	ACTION					GOTO
	a	b	c	d	$	S	A	B
0		s3		s59		1	2	4
1					acc
2	s6
3				s59			7	8
4			s9
59	r5|r6		r5|r6
6					r1
7			s10
8	s11
9					r3
10					r2
11					r4

可见该分析表中存在二义性的条目，故该文法不是LALR（1）文法

语法制导的翻译

5.1.2

扩展图 5-4 中的 SDD，使它可以像图 5-1 所示的那样处理表达式

	产生式	语义规则
1)	$L\to En$	$L.val=E.val$
2)	$E\to T{E}^{\prime }$	$E^{\prime }.inh=T.val$ $E.val=E^{\prime }.syn$
3)	$E^{\prime }\to +T{E}_1^{\prime }$	$E_1^{\prime }.inh=E^{\prime }.inh+T.val$ $E^{\prime }.syn=E_1^{\prime }.syn$
4)	$E^{\prime }\to \epsilon$	$E^{\prime }.syn=E^{\prime }.inh$
5)	$T\to F{T}^{\prime }$	$T^{\prime }.inh=F.val$ $T.val=T^{\prime }.syn$
6)	$T^{\prime }\to \ast F{T}_1^{\prime }$	$T_1^{\prime }.inh=T_1^{\prime }.inh\ast F.val$ $T^{\prime }.syn=T_1^{\prime }.syn$
7)	$T^{\prime }\to \epsilon$	$T^{\prime }.syn=T^{\prime }.inh$
8)	$F\to (E)$	$F.val=E.val$
9)	$F\to digit$	$F.val=digit.lexval$

(3+4)*(5+6)n 语法分析树

5.2.2

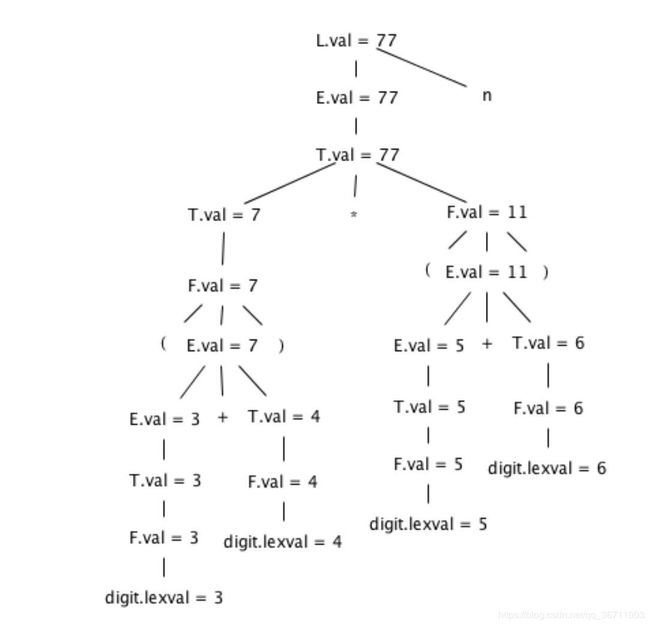
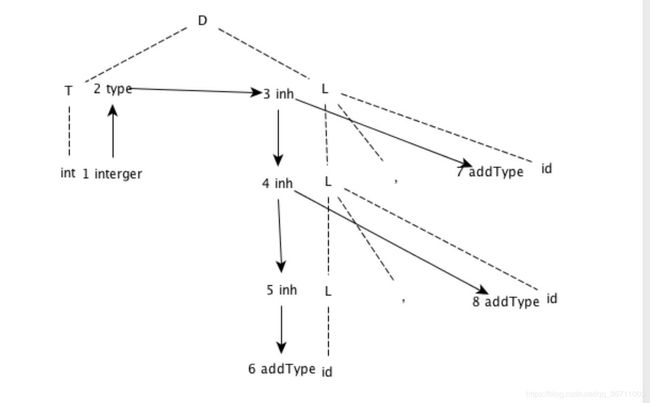
对于图 5-8 中的 SDD，给出下列表达式对应的注释语法分析树：

1. int a, b , c

5.2.4

这个文法生成了含“小数点”的二进制数：

    S -> L.L|L
    L -> LB|B
    B -> 0|1

设计一个 L 属性的 SDD 来计算 S.val，即输入串的十进制数值。比如，串 101.101 应该被翻译为十进制数 5.625。

L具有继承属性side和综合属性m

L.side表示小数点的左边或右边(1表示左边0表示右边)，L.m二进制串的长度即幂次。

	产生式	语义规则
1)	$S\to L_1.L_2$	$L_1.side=1$ $L_2.side=0$ $S.val=L_1.val+L_2.val$
2)	$S\to L$	$L.side=1$ $S.val=L.val$
3)	$L\to L_{1}B$	$L_1.side=L.side$ $L.m=L_1.m+1$ $L.val=L_1.side?L_1.val\ast 2+B.val:L1.val+B.val>>m$
4)	$L\to B$	$L.m=1$ $L.val=L.side?B.val:B.val/2$
5)	$B\to 0$	$B.val=0$
6)	$B\to 1$	$B.val=1$

5.4.3

下面的 SDT 计算了一个由 0 和 1 组成的串的值。它把输入的符号串当做正二进制数来解释。

$B\to B_{1}0\{B.val=2\ast B_1.val\}$
$|B_{1}1\{B.val=2\ast B_1.val+1\}$
$|1\{B.val=1\}$

改写这个 SDT，使得基础文法不再是左递归的，但仍然可以计算出整个输入串的相同的 B.val 的值。

1. 提取左公共因子

$$\begin{gathered} B\to B_{1}digit\{B.val=2\ast B_1.val+digit.val\} \\ |1\{B.val=1\} \end{gathered}$$
$$\begin{gathered} digit\to 0\{digit.val=0\} \\ |1\{digit.val=1\} \end{gathered}$$

2. 消除左递归

	B -> 1 {A.i = 1}A
	A -> digit {A_1.i = 2*A.i + digit.val}A_1 {A.val = A_1.i}
	A -> ε {A.val = A.i}
	digit -> 0 {digit.val = 0}
	digit -> 1 {digit.val = 1}