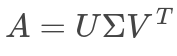Spark分布式机器学习源码分析：奇异值分解（SVD）与主成分分析（PCA）

原理    Spark是一个极为优秀的大数据框架，在大数据批处理上基本无人能敌，流处理上也有一席之地，机器学习则是当前正火热AI人工智能的驱动引擎，在大数据场景下如何发挥AI技术成为优秀的大数据挖掘工程师必备技能。本文结合机器学习思想与Spark框架代码结构来实现分布式机器学习过程，希望与大家一起学习进步～

    本文采用的组件版本为：Ubuntu 19.10、Jdk 1.8.0_241、Scala 2.11.12、Hadoop 3.2.1、Spark 2.4.5，老规矩先开启一系列Hadoop、Spark服务与Spark-shell窗口：

    降维是减少所考虑变量数量的过程。它可用于从原始和嘈杂的特征中提取潜在特征，或者在保持结构的同时压缩数据。spark.mllib为RowMatrix类提供降维支持。

1

SVD介绍

    奇异值分解（SVD）将矩阵分解为三个矩阵：U，Σ和V，使得：

    这里U是一个正交矩阵，其列称为左奇异向量，Σ是对角矩阵，其中非对角线按降序排列，其对角线称为奇异值，V是一个正交矩阵，其列称为右奇异向量。

    对于大型矩阵，通常不需要完整的因式分解，而仅需要顶部奇异值及其关联的奇异矢量。这样可以节省存储空间，降低噪声并恢复矩阵的低阶结构。如果我们保留前k个奇异值，那么所得的低秩矩阵的维将为：

• U：m*k

• Σ：k*k

• V：n*k

    我们假设n小于m。奇异值和右奇异向量是从Gramian矩阵ATA的特征值和特征向量得出的。如果用户通过computeU参数请求，则通过矩阵乘法将存储左奇异矢量Ui的矩阵计算为U = A（VS-1）。实际使用的方法是根据计算成本自动确定的：

• 如果n小（n <100）或k与n（k> n / 2）相比较大，我们首先计算Gramian矩阵，然后在驱动程序上局部计算其最高特征值和特征向量。这需要在每个执行器和驱动程序上进行一次O（n2）存储操作，并在驱动程序上进行O（n2k）时间处理。

• 否则，我们将以分布式方式计算（ATA）v并将其发送到ARPACK，以计算驱动程序节点上（ATA）的最高特征值和特征向量。这需要O（k）次通过，每个执行程序上的O（n）存储以及驱动程序上的O（nk）存储。

2

SVD实例

    spark.mllib为RowMatrix类中提供的面向行的矩阵提供SVD功能。

import org.apache.spark.mllib.linalg.Matrix
import org.apache.spark.mllib.linalg.SingularValueDecomposition
import org.apache.spark.mllib.linalg.Vector
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.linalg.distributed.RowMatrix
// 定义数组
val data = Array(
  Vectors.sparse(5, Seq((1, 1.0), (3, 7.0))),
  Vectors.dense(2.0, 0.0, 3.0, 4.0, 5.0),
  Vectors.dense(4.0, 0.0, 0.0, 6.0, 7.0))
val rows = sc.parallelize(data)
val mat: RowMatrix = new RowMatrix(rows)
// 计算前5个奇异值和相应的奇异向量。
val svd: SingularValueDecomposition[RowMatrix, Matrix] = mat.computeSVD(5, computeU = true)
val U: RowMatrix = svd.U  // U因子
val s: Vector = svd.s     // 奇异值存储在一个本地dense向量中
val V: Matrix = svd.V     // V因子

3

SVD源码分析

    计算SVD的源码如下：

def computeSVD(
      k: Int,
      computeU: Boolean = false,
      rCond: Double = 1e-9): SingularValueDecomposition[RowMatrix, Matrix] = {
    // 迭代次数
    val maxIter = math.max(300, k * 3)
    // 阈值
    val tol = 1e-10
    computeSVD(k, computeU, rCond, maxIter, tol, "auto")
}

    computeSVD(k, computeU, rCond, maxIter, tol, "auto")的实现分为三步。分别是选择计算模式，特征值分解，计算V,U,Sigma。下面分别介绍这三步。首先是选择计算模式：

 val computeMode = mode match {
      case "auto" =>
        if (k > 5000) {
          logWarning(s"computing svd with k=$k and n=$n, please check necessity")
        }
        if (n < 100 || (k > n / 2 && n <= 15000)) {
          // 满足上述条件，首先计算方阵，然后本地计算特征值，避免数据传递
          if (k < n / 3) {
            SVDMode.LocalARPACK
          } else {
            SVDMode.LocalLAPACK
          }
        } else {
          // 分布式实现
          SVDMode.DistARPACK
        }
      case "local-svd" => SVDMode.LocalLAPACK
      case "local-eigs" => SVDMode.LocalARPACK
      case "dist-eigs" => SVDMode.DistARPACK
 }

    特征值分解：

 val (sigmaSquares: BDV[Double], u: BDM[Double]) = computeMode match {
      case SVDMode.LocalARPACK =>
        val G = computeGramianMatrix().toBreeze.asInstanceOf[BDM[Double]]
        EigenValueDecomposition.symmetricEigs(v => G * v, n, k, tol, maxIter)
      case SVDMode.LocalLAPACK =>
        // breeze (v0.10) svd latent constraint, 7 * n * n + 4 * n < Int.MaxValue
        val G = computeGramianMatrix().toBreeze.asInstanceOf[BDM[Double]]
        val brzSvd.SVD(uFull: BDM[Double], sigmaSquaresFull: BDV[Double], _) = brzSvd(G)
        (sigmaSquaresFull, uFull)
      case SVDMode.DistARPACK =>
        if (rows.getStorageLevel == StorageLevel.NONE) {
          logWarning("The input data is not directly cached, which may hurt performance if its"
            + " parent RDDs are also uncached.")
        }
        EigenValueDecomposition.symmetricEigs(multiplyGramianMatrixBy, n, k, tol, maxIter)
    }

    计算U,V以及Sigma：

//获取特征值向量
    val sigmas: BDV[Double] = brzSqrt(sigmaSquares)
    val sigma0 = sigmas(0)
    val threshold = rCond * sigma0
    var i = 0
    // sigmas的长度可能会小于k
    // 所以使用 i < min(k, sigmas.length) 代替 i < k.
    if (sigmas.length < k) {
      logWarning(s"Requested $k singular values but only found ${sigmas.length} converged.")
    }
    while (i < math.min(k, sigmas.length) && sigmas(i) >= threshold) {
      i += 1
    }
    val sk = i
    if (sk < k) {
      logWarning(s"Requested $k singular values but only found $sk nonzeros.")
    }
    //计算s，也即sigma
    val s = Vectors.dense(Arrays.copyOfRange(sigmas.data, 0, sk))
    //计算V
    val V = Matrices.dense(n, sk, Arrays.copyOfRange(u.data, 0, n * sk))
    //计算U
    // N = Vk * Sk^{-1}
    val N = new BDM[Double](n, sk, Arrays.copyOfRange(u.data, 0, n * sk))
    var i = 0
    var j = 0
    while (j < sk) {
        i = 0
        val sigma = sigmas(j)
        while (i < n) {
          //对角矩阵的逆即为倒数
          N(i, j) /= sigma
          i += 1
        }
        j += 1
    }
    //U=A * N
    val U = this.multiply(Matrices.fromBreeze(N))

4

PCA介绍

    主成分分析是最常用的一种降维方法。我们首先考虑一个问题：对于正交矩阵空间中的样本点，如何用一个超平面对所有样本进行恰当的表达。容易想到，如果这样的超平面存在，那么他大概应该具有下面的性质。    基于最近重构性和最大可分性，能分别得到主成分分析的两种等价推导。

• 最近重构性：样本点到超平面的距离都足够近

• 最大可分性：样本点在这个超平面上的投影尽可能分开

   主成分分析（PCA）是一种统计方法，用于查找旋转，以使第一个坐标具有最大的方差，而每个后续坐标又具有最大的方差。旋转矩阵的列称为主成分。PCA被广泛用于降维。spark.mllib支持将PCA用于以行格式和任何Vector存储的高而瘦的矩阵。

5

PCA实例

    以下代码演示了如何在RowMatrix上计算主成分并将其用于将向量投影到低维空间中。

import org.apache.spark.mllib.linalg.Matrix
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.linalg.distributed.RowMatrix
val data = Array(
  Vectors.sparse(5, Seq((1, 1.0), (3, 7.0))),
  Vectors.dense(2.0, 0.0, 3.0, 4.0, 5.0),
  Vectors.dense(4.0, 0.0, 0.0, 6.0, 7.0))
val rows = sc.parallelize(data)
val mat: RowMatrix = new RowMatrix(rows)
// 计算4个主成分
// 主成分存储在本地dense矩阵中
val pc: Matrix = mat.computePrincipalComponents(4)
// 将行投影到前4个主要成分所跨越的线性空间
val projected: RowMatrix = mat.multiply(pc)

6

PCA源码分析

    主成分分析的实现代码在RowMatrix中实现。源码如下：

def computePrincipalComponents(k: Int): Matrix = {
    val n = numCols().toInt
    //计算协方差矩阵
    val Cov = computeCovariance().toBreeze.asInstanceOf[BDM[Double]]
    //特征值分解
    val brzSvd.SVD(u: BDM[Double], _, _) = brzSvd(Cov)
    if (k == n) {
      Matrices.dense(n, k, u.data)
    } else {
      Matrices.dense(n, k, Arrays.copyOfRange(u.data, 0, n * k))
    }
  }

    这段代码首先会计算样本的协方差矩阵，然后在通过breeze的svd方法进行奇异值分解。这里由于协方差矩阵是方阵，所以奇异值分解等价于特征值分解。下面是计算协方差的代码：

def computeCovariance(): Matrix = {
    val n = numCols().toInt
    checkNumColumns(n)
    val (m, mean) = rows.treeAggregate[(Long, BDV[Double])]((0L, BDV.zeros[Double](n)))(
      seqOp = (s: (Long, BDV[Double]), v: Vector) => (s._1 + 1L, s._2 += v.toBreeze),
      combOp = (s1: (Long, BDV[Double]), s2: (Long, BDV[Double])) =>
        (s1._1 + s2._1, s1._2 += s2._2)
    )
    updateNumRows(m)
    mean :/= m.toDouble
    // We use the formula Cov(X, Y) = E[X * Y] - E[X] E[Y], which is not accurate if E[X * Y] is
    // large but Cov(X, Y) is small, but it is good for sparse computation.
    // TODO: find a fast and stable way for sparse data.
    val G = computeGramianMatrix().toBreeze.asInstanceOf[BDM[Double]]
    var i = 0
    var j = 0
    val m1 = m - 1.0
    var alpha = 0.0
    while (i < n) {
      alpha = m / m1 * mean(i)
      j = i
      while (j < n) {
        val Gij = G(i, j) / m1 - alpha * mean(j)
        G(i, j) = Gij
        G(j, i) = Gij
        j += 1
      }
      i += 1
    }
    Matrices.fromBreeze(G)
  }

    Spark 降维算法的内容至此结束，有关Spark的基础文章可参考前文：

    Spark分布式机器学习源码分析：矩阵向量

    Spark分布式机器学习源码分析：基本统计

    Spark分布式机器学习源码分析：线性模型

    Spark分布式机器学习源码分析：朴素贝叶斯

    Spark分布式机器学习源码分析：决策树模型

    Spark分布式机器学习源码分析：集成树模型

    Spark分布式机器学习源码分析：协同过滤

    Spark分布式机器学习源码分析：K-means

    Spark分布式机器学习源码分析：隐式狄利克雷分布（LDA）

    参考链接：

    http://spark.apache.org/docs/latest/mllib-clustering.html

    https://github.com/endymecy/spark-ml-source-analysis

历史推荐

“高频面经”之数据分析篇

“高频面经”之数据结构与算法篇

“高频面经”之大数据研发篇

“高频面经”之机器学习篇

“高频面经”之深度学习篇

爬虫实战：Selenium爬取京东商品

爬虫实战：豆瓣电影top250爬取

爬虫实战：Scrapy框架爬取QQ音乐

数据分析与挖掘

数据结构与算法

机器学习与大数据组件

欢迎关注，感谢“在看”，随缘稀罕~

 

一个赞，晚餐加鸡腿