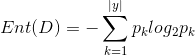机器学习实战(Peter Harrington)----决策树
决策树:一种一层一层去进行判决、分类的方法
核心:决策树的构造
(Reference:周志华--机器学习--第四章-机器学习)
在决策树的构造中,实际上就是通过一层一层的划分,将整个数据集划分为许多个分支。在这个过程中,我们希望的是在不断划分的过程里面每个分支的内容会越来越“纯”,也就是每个分支节点所包含的样本尽可能是属于同一个类别的。为了达到这个目的,在每一个分支节点我们需要选择根据哪一个特征值来对这一个节点子集进行数据划分,从而尽力达到提高“纯度”的目的,这里就涉及到了“信息增益”这一概念。如果根据某一属性对当前节点进行划分后,所得到的信息增益越大,则表明“纯度提升”越大。
在计算信息增益时,需要了解另一个概念“信息熵”,假定当前样本集合D中第k类样本所占的比例为![]() ,则D的信息熵定义为:
,则D的信息熵定义为:
其中,![]() 的值越小则意味着D的“纯度”越高。
的值越小则意味着D的“纯度”越高。
对信息熵这一概念有了理解之后,我们再引入信息增益概念。
由信息熵的定义,我们知道对于每一个样本集合来说我们都可以求取它对应的信息熵值,那么对于决策树分支节点的划分来说,对于划分前的父节点,我们可以计算其对应的信息熵值,而对于划分后的各个子节点,我们也可以对其分别求取信息熵,然后求和得到划分后的总信息熵值,二者相减就会得到该划分的信息增益。注意,在计算子节点信息熵和值时,由于各个子节点中包含的样本数目是不同的,因此我们应该根据各个子节点中包含的样本数目来给对应的子节点熵值一个权重,即![]() ,即包含元素越多的子节点在熵值中贡献越大。因而可以得到“信息增益”公式,如下:
,即包含元素越多的子节点在熵值中贡献越大。因而可以得到“信息增益”公式,如下:
根据![]() 的值越小则意味着D的“纯度”越高,我们可以知道对于信息增益来说,
的值越小则意味着D的“纯度”越高,我们可以知道对于信息增益来说,![]() 的值越大则意味着使用特征a划分D所获得的“纯度提升”越大。
的值越大则意味着使用特征a划分D所获得的“纯度提升”越大。
以上就是关于信息熵和信息增益的介绍,下面来介绍具体的算法实现以及相应的应用。
信息熵:
def calcShannonEnt(dataSet):
'''
Calculating the Shannon entropy of a given data set
input: dataSet(mat) given data set
output: shannonEnt(float) Shannon entropy
'''
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
# storage every key and number of occurrences
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries
shannonEnt -= prob * log(prob, 2)
return shannonEnt需要注意的是,我们在这里使用的数据是如下所示的类型:
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing','flippers']
return dataSet, labels可以看到,for循环是对集合中的每个类别的数据进行统计,并使用字典存储所有的类别以及对应的出现次数,最后求取每个类别对应的概率并依据公式(1)求取该集合的信息熵值。
选取最佳划分依据:
在介绍选取最佳划分依据函数之前,需要介绍一下另一个函数splitDataSet,该函数的功能是根据指定的特征i和对应的特征值value来对dataSet进行划分,其源码如下:
def spiltDataSet(dataSet, axis, value):
'''
According given feature to split dataSet
input: dataSet(mat) dataSet which wait to split
axis(int) index of feature
value() return value of feature
output: retDataSet(mat)
'''
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet可以看到,这个函数的作用就是根据传入的特征索引axis(即第几个特征)和特征值value,从而取出dataSet中第axis个特征值为value的部分,并将这些部分去除掉第axis个特征后返回。
def chooseBestFeatureToSplit(dataSet):
'''
choose best way to split dataSet
input:
output:
gain number of feature
'''
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = spiltDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if infoGain > bestInfoGain:
# newEntropy less than last entropy
bestInfoGain = infoGain
bestFeature = i
return bestFeature从信息增益的介绍中我们可以知道,在进行字节点划分时,根据不同的特征来划分子节点,最终得到的不同子节点信息熵值时不同的,也就是“纯度”不同,因此,我们在划分子节点时就需要选择一个合适的划分依据---即特征,来进行字节点的划分以求得到最大的“纯度”。上面的代码就是为了得到最佳的划分依据。
该函数会遍历dataSet中的每个特征,并根据每个特征值来对数据集进行划分,求取每个划分结果的信息熵,选取结果中信息熵最小的那个划分结果,该结果对应的划分依据(即对应的特征)就是最优的依据。(需要注意的是,这里采用的比较内容是子集的信息熵值,而不是整个划分过程的信息增益,因此应该是信息熵值越小,表明这个划分结果越优秀)
创建决策树:
上面我们已经介绍过了计算信息熵和选取最佳分类依据等内容,下面我们将进行决策树的创建。
在这里,我们需要先介绍一个函数majorityCnt(classList),该函数的功能是返回在classList中出现次数最多的类别,源码如下:
def majorityCnt(classList):
'''
count the most frequently occurring tags
input: classList(list) list of category names
output: sorrtedClassCount[0][0](str) most frequently category name
'''
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sorrtedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True)
return sorrtedClassCount[0][0]下面我们介绍决策树的创建部分:
def createTree(dataSet,labels):
'''
create determine tree
input: dataSet(mat)
labels(vec)
output: myTree(dic) final tree(Strored as a dictionary)
'''
classList = [example[-1] for example in dataSet]
# the role of count is to count the number of occurrences of a string in a string
# only when every string same to the first string, function will return in here
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(spiltDataSet(dataSet, bestFeat, value), subLabels)
return myTree
总体流程:
1.计算一个最佳的分类特征,将该特征对应的标签作为父节点,并在Labels中删掉这个标签;
2.遍历该特征对应的所有特征值,根据每个特征值使用spiltDataSet函数将数据集进行子集合划分,随后递归调用createTree函数继续进行树的创建。
在这里,特征和label之间是有对应关系的,这取决于你的数据结构,在这里我们使用的数据如下图:
参考我们在信息熵中对数据类型的介绍,就会明白该表和数据类型的对应关系。
需要注意的是:
在程序中我们有两个判断返回部分,这是树创建结束标志,分别如下:
if classList.count(classList[0]) == len(classList):
return classList[0]这部分的条件是对于传入的数据集来说,如果所有的标签都属于一个类别,比如说按照上面的数据类别,如果一个集合中所有的样本都属于鱼类,那么就不需要继续往下创建树,因为我们已经得到了我们想要的结果,classList.count是统计某个list中出现次数最多的元素出现的次数。
if len(dataSet[0]) == 1:
return majorityCnt(classList)这部分的条件是对于传入的数据集来说,如果只剩下一个特征值可以用,那么就直接返回在该特征值中出现频率最高的那一类,这部分可能有点拗口,具体来说就是对于上面的数据类型来说,dataSet[0] = 3,也就是说特征个数是3个,如果一层一层的进行决策最后只剩下一个特征即"是否属于鱼类",这时候,我们直接选取在这个特征值中出现次数最多的作为结果,也就是“否”。