算法:(BFS)迷宫寻路算法
来自蓝桥杯oj
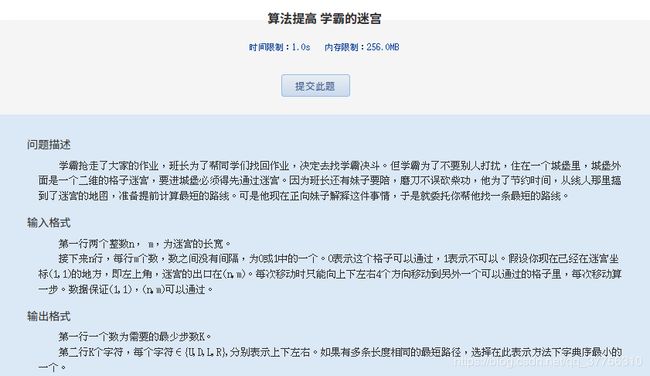

解法
这一题属于典型的迷宫搜索类题,刚入手时我也是一脸茫然,但是仔细思考了一晚上,还是勉强的解决了,这道题属于经典的BFS搜索题,解决的核心在于,如何找到迷宫出口,还有如何存储路径
解法1:BFS+路径存储
作为图论中经典的搜索算法之一,BFS算法搜索路径的特点是"层层搜索",映射到这个题目上,给我的理解就是,使用BFS这个特点,一旦我们搜索到终点,好吧,整个过程也可以结束了,因为BFS每一步的遍历都是基于全局考虑的,所以一旦搜索到终点,不用想了,搜索的次数一定是最短的,基于这个特点,对于第一行要求输出最短路径数,我们就可以根据这个特点来计算,对于第二行要我们输出路径,这也很好办,我们只需要在结点类里再封装两个属性(当前所走的轨迹,上一个结点的信息)
//结点类
class N{
int x;//当前结点的横坐标
int y;//当前结点的纵坐标
N pre;//前趋结点,用来回溯路径
String dir;//用于输出方向信息
N(int x,int y,String d,N pr){
this.x = x;
this.y = y;
this.dir = d;
this.pre = pr;
}
}
下面我们来实现这个算法,BFS遍历需要借助的数据结构是队列,所以我们使用Java里已经封装好的Queue,上一段刚刚已经AC的code
/**
*
* @param map 地图
* @param n 地图长度
* @param m 地图宽度
*/
static void BFS(int[][] map,int n,int m) {
/*
* 使用广度优先策略
*/
/*
* 方向数组
*/
int[][] dis = {
{1,0},//下
{0,-1},//左
{0,1},//右
{-1,0},//上
};
/*
* 轨迹数组,注意,一定要与dis数组相对应
* 思考,为什么一定要按这个顺序?因为题目给出路径输出要按字典序输出,所以我们要优先将字典序小的"方向字母"先入队(先访问)
*/
String[] str = {"D","L","R","U"};
/*
* 标记数组,用于判断当前结点是否已经访问
*/
int[][] book = new int[n+1][m+1];
/*
* 队列
*/
Queue Q = new LinkedList();
Q.add(new N(1,1,"",null));//起点入队
book[1][1] = 1;//标记已经走过了
while(!Q.isEmpty()) {//如果队列不为空,还可继续遍历
N p = Q.peek();//寻找下一步可以走的结点
for(int i=0;i<4;i++) {
//遍历四个方向
int x = p.x+dis[i][0];
int y = p.y+dis[i][1];
//边界判断
if(x<1 || x>n || y<1 || y>m || map[x][y]==1 || book[x][y]==1) {
continue;
}
if(map[x][y]==0 && book[x][y]==0) {
//找到可以走的结点,入队
Q.add(new N(x,y,str[i],p));
if(x==n && y==m) {
//如果此时已经到达终点,开始输出路径
N temp = Q.peek();
int step = 0;//记录最小步数
StringBuffer ans = new StringBuffer();//由于是逆序(从终点到起点)记载路径,所以我们最终还要使用append反转一下
if(temp.x+1 == n) {//因为会出现最后一步无法打印路径的情况,需要手动判断一下
ans.append("D");
}else if(temp.y+1 == m) {
ans.append("R");
}
while(temp!=null) {
ans.append(temp.dir);
step++;
temp = temp.pre;
}
System.out.println(step);
System.out.println(ans.reverse().toString());
return;
}
book[x][y] = 1;//此时标记已经访问
}
}
Q.poll();
}
}
解法二:DFS+路径存储
这道也可以用DFS来解决,但是逻辑相对较混乱,AC之后也只有30分,自己不是vip也看不到评测数据,感觉自己测的时候没啥问题啊(* 0 *),有点迷茫
/***
*
* @param map 地图
* @param n 地图的长
* @param m 地图的宽
*/
static void DFS(int[][] map,int n,int m) {
/*
* 方向数组
*/
int[][] dis = {
{-1,0},//上
{0,1},//右
{0,-1},//左
{1,0},//下
};
/*
* 路径输出数组,注意此时要按字典序从大到小遍历顺序来排,因为栈是后进先出的,越早入栈越晚遍历到
*/
String[] str = {"U","R","L","D"};
int[][] book = new int[n+1][m+1];
Stack S = new Stack();
N begin = new N(1,1,"",null);
S.push(begin);//把迷宫入口推入栈中,并标记已经访问
book[1][1]=1;
while(!S.isEmpty()) {//如果栈不为空,还可以继续遍历
N p = S.pop();//弹出第一个元素
for(int i=0;i<4;i++) {
//枚举四个方向
int x = p.x+dis[i][0];
int y = p.y+dis[i][1];
//边界判断
if(x<1 || x>n || y<1 || y>m || map[x][y]==1 || book[x][y]==1) {
continue;
}
if(map[x][y] == 0 && book[x][y] == 0) {
if(x==n && y==m) {
//终点判断
S.push(new N(x,y,str[i],p));
N tail = S.peek();
StringBuffer ans = new StringBuffer();//依旧是append后反转一下输出
int t = 0;
while(tail.pre!=null) {
ans.append(tail.dir);
t++;
tail = tail.pre;
}
System.out.println(t);
System.out.println(ans.reverse().toString());
return;
}
S.push(new N(x,y,str[i],p));
book[x][y] = 1;
}
}
}
}
Main函数
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
int[][] map = new int[n+1][m+1];
for(int i=1;i<=n;i++) {
String st = in.next();
for(int j=1;j<=m;j++) {
map[i][j] = Integer.parseInt( (String.valueOf(st.charAt(j-1))));//这个要强转一下,字符转成整数
}
}
DFS(map, n, m);
BFS(map, n, m);
}
这道题花了我很长的时间来思考,难点在于,这道题是广搜的升级版,考虑到了路径存储,既要保证路径正确不能走错,还要考虑字典序输出,算法还可待优化,希望有大佬可指教。
