【泛读】NIPS- Break the Ceiling:Stronger Multi-scale Deep GCNs
Break the Ceiling:Stronger Multi-scale Deep GCNs Whats the problem?
现存的图神经网络没有充分利用多尺度信息和深层架构。
1.如果基于GCN架构增加层数,提取的特征最多保留图结构的固定信息,并且丢失节点特征中的所有信息。
2.ReLU是一个阴谋家。
代码链接
How to solve them?
作者证明了任何具有明确定义的解析光谱滤波器的图卷积都可以写为块Krylov矩阵和特殊形式的可学习参数矩阵的乘积。基于这些分析,作者提出了两种GCN架构,它们以不同的方式利用多尺度信息,并且可以扩展到更深更丰富的结构,期望具有更强的表达能力和能力来提取图结构化数据的更丰富的表示形式。
作者首先构建了一个块krylov子空间形式的深层GCN。假设有一系列解析光谱滤波器 G = g 0 , g 1 , . . . g n G={g_0,g_1,...g_n} G=g0,g1,...gn和一系列逐点的非线性激活函数 H = h 0 , h 1 , . . . , h n H={h_0,h_1,...,h_n} H=h0,h1,...,hn,那么: Y = s o f t m a x { g n ( L ) h n − 1 { . . . g 2 ( L ) h 1 { g 1 ( L ) h 0 { g 0 L X W 0 ′ } W 1 ′ } W 2 ′ . . . } W n ′ } Y=softmax\{g_n(L)h_{n-1}\{...g_2(L)h_1\{g_1(L)h_0\{g_0{L}XW_0^{'}\}W_1^{'}\}W_2^{'}...\}W_n^{'}\} Y=softmax{gn(L)hn−1{...g2(L)h1{g1(L)h0{g0LXW0′}W1′}W2′...}Wn′} 不难看出,当 g i ( L ) = A ~ , n = 1 g_i(L)=\widetilde{A},n=1 gi(L)=A ,n=1时,这就是普通的GCN。但是这样设计的深层结构有难以计算的问题。虽然直接在GCN中实现块Krylov方法是困难的,但是这启发作者在每一层中堆砌多尺度信息,这样网络将有能力拓展到深层结构。作者提出了两个结构:snowball和truncated Krylov。这些方法在隐层中以不同方式连接多尺度特征信息,同时两者都有可能被扩展到更深层次的体系结构。
1.Snowball
为了将多尺度特征连接在一起,得到每个节点更丰富的表示,作者设计了一个密集连通图网络如下: H 0 = X , H l + 1 = f ( L [ H 0 , H 1 , . . . , H l ] W l ) , l = 0 , 1 , 2 , . . . , n − 1 C = g ( [ H 0 , H 1 , . . . , H n ] W n ) o u t p u t = s o f t m a x ( L p C W c ) H_0=X,H_{l+1}=f(L[H_0,H_1,...,H_l]W_l),l=0,1,2,...,n-1\\C=g([H_0,H_1,...,H_n]W_n)\\output=softmax(L^pCW_c) H0=X,Hl+1=f(L[H0,H1,...,Hl]Wl),l=0,1,2,...,n−1C=g([H0,H1,...,Hn]Wn)output=softmax(LpCWc) 其中 W l , W n , W c W_l,W_n,W_c Wl,Wn,Wc是可学习的参数矩阵, F l + 1 F_{l+1} Fl+1是 l l l层的输出通道数, f , g f,g f,g是激活函数, C C C是任何类型的分类器, p ∈ { 0 , 1 } p\in\{0,1\} p∈{0,1}, H 0 , H 1 , . . , H n H_0,H_1,..,H_n H0,H1,..,Hn是提取的特征。当 p = 0 , L P = I p=0,L^P=I p=0,LP=I或者 p = 1 , L p = L p=1,L^p=L p=1,Lp=L时,意味着C投影回图的Fourier基上,这在图结构编码大量信息时是必要的。基于此,可以堆砌学习过的特征作为下一层的输入。这样一来,输入的尺度将会像snowball一样越来越大,这和DenseNet很像。因此,DenseNet的一些优点是自然继承的,例如减轻了消失梯度问题,鼓励了特征重用,增加了每个隐藏层的输入变化,减少了参数数目,加强了特征传播,提高了模型的紧凑性。
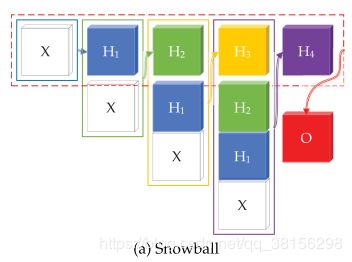
2.Truncated Krylov
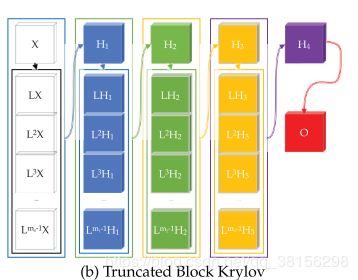
截断块Krylov网络可以表示为:
H 0 = X , H l + 1 = f ( [ H l , L H l , . . . , L m l − 1 H l ] W l ) , l = 0 , 1 , 2 , . . . , n − 1 C = g ( H n W n ) o u t p u t = s o f t m a x ( L p X W C ) H_0=X,H_{l+1}=f([H_l,LH_l,...,L^{m_l-1}H_l]W_l),l=0,1,2,...,n-1\\C=g(H_nW_n)\\output=softmax(L^pXW_C) H0=X,Hl+1=f([Hl,LHl,...,Lml−1Hl]Wl),l=0,1,2,...,n−1C=g(HnWn)output=softmax(LpXWC)
作者不是对特定的函数或固定的X进行截断,而是在训练中处理变量X。因此,我们不能对X及其与L的关系作任何限制,以得到一个实际的误差界。
Ideas u can learn
- 逐点ReLU效果不好,Tanh在保持列特征之间的线性独立性方面更好。提议用Tanh替换ReLU。
- 可以考虑Snowball一样,结合多尺度的特征进行训练。
New knowledge
1.GCNs为什么没有必要更深?
原因一:图卷积其实是拉普拉斯平滑的一种特殊形式,有多层卷积的网络会导致过拟合问题,这使得即使对于彼此远离的节点,也无法区分节点的表示。
原因二:对于许多案例,对于标签信息没有必要遍历整张图。而且,可以对输入图进行多尺度粗化,并获得与具有更多层的GCN相同的信息流。
虽然如此,浅层学习机制违反了深度学习的组成原则,并限制了标签传播。