玩平衡车系列——直流电机PID开发指南
(基于平衡小车之家标准版)
0.PID简介
PID 调节器出现于上世纪 30 年代。所谓 PID 控制,就是对偏差进行比例、积分和微分的控制。PID 由 3 个单元组成,分别是比例(P)单元、积分(I)单元、微分(D)单位。在工程实践中,一般 P 是必须的,所以衍生出许多组合的PID 控制器,如 PD、PI、PID 等。
在我们的微处理器里面,因为控制器是通过软件实现其控制算法的,所以必须对模拟调节器进行离散化处理,这样它只需根据采样时刻的偏差值计算控制量。因此,我们需要使用离散的差分方程代替连续的微分方程。假定采样时间很短时(比如10ms),可做如下处理:
1) 用一介差分代替一介微分;
2) 用累加代替积分
1.位置闭环控制
位置闭环控制就是根据编码器的脉冲累加测量电机的位置信息,并与目标值进行比较,得到控制偏差,然后通过对偏差的比例、积分、微分进行控制,使偏差趋向于零的过程。
1.1 理论分析
根据位置式离散 PID 公式:
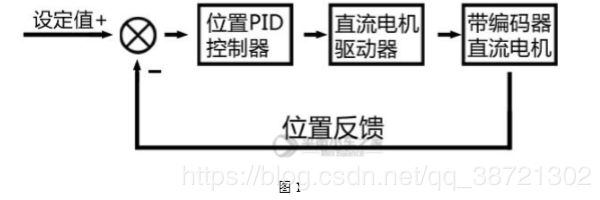
1.2 控制原理图
图 1 为位置控制原理图。其中需要说明的是,我们这边是通过微机实现 PID控制的,所以下面的【位置 PID 控制器】是一个软件实现的过程,比如在我们的代码里面就是一个我们定义的函数。
/**************************************************************************
函数功能:位置式PID控制器
入口参数:编码器测量位置信息,目标位置
返回 值:电机PWM
根据位置式离散PID公式
pwm=Kp*e(k)+Ki*∑e(k)+Kd[e(k)-e(k-1)]
e(k)代表本次偏差
e(k-1)代表上一次的偏差
∑e(k)代表e(k)以及之前的偏差的累积和;其中k为1,2,,k;
pwm代表输出
**************************************************************************/
int Position_PID (int Encoder,int Target)
{
static float Bias,Pwm,Integral_bias,Last_Bias;
Bias=Encoder-Target; //计算偏差
Integral_bias+=Bias; //求出偏差的积分
Pwm=Position_KP*Bias+Position_KI*Integral_bias/10+Position_KD*(Bias-Last_Bias); //位置式PID控制器
Last_Bias=Bias; //保存上一次偏差
return Pwm; //增量输出
}
//第一行是相关内部变量的定义。
//第二行是求出速度偏差,由测量值减去目标值。
//第三行通过累加求出偏差的积分。
//第四行使用位置式 PID 控制器求出电机 PWM。
//第五行保存上一次偏差,便于下次调用。
//最后一行是返回。
//然后,在定时中断服务函数里面调用该函数实现我们的控制目标:
Moto=Position_PID(Encoder,Target_Position);
Set_Pwm(Moto); //===赋值给 PWM 寄存器
1.4 参数整定
首先我们需要明确我们的控制目标,也就是满足控制系统的 3 个要求:
- 稳定性
- 快速性
- 准确性
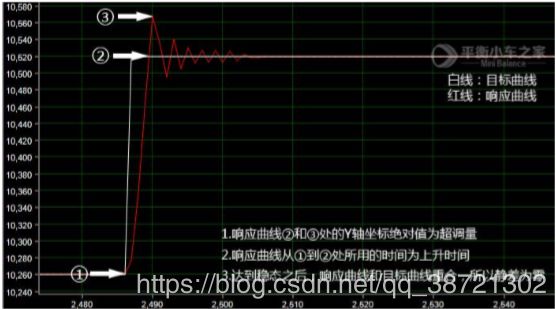
具体的评估指标有最大超调量、上升时间、静差等。
最大超调量是响应曲线的最大峰值与稳态值的差,是评估系统稳定性的一个重要指标;上升时间是指响应曲线从原始工作状态出发,第一次到达输出稳态值所需的时间,是评估系统快速性的一个重要指标;静差是被控量的稳定值与给定值之差,一般用于衡量系统的准确性,具体可以参考图 2 的解析。
下面我们使用【平衡小车之家】直流电机 PID 学习套件 1.0 进行 PID 参数整定实验,使用套件的控制板上面的按键调节 PID 参数,然后通过观察上位机响应曲线,并评估控制效果,给出 PID 调节的心得。
关于 P、I、D 三个参数的主要作用,可以大致又不完全地概况为:P 用于提高响应速度、I 用于减小静差、D 用于抑制震荡。
下面我们把控制目标从 10000 上升至 10260 时,观察响应曲线的变化。一般我们进行 PID 参数整定的时候,首先设 I 和 D 值为零,然后把 P 值从 0 逐渐增大,直到系统震荡结束。
① KP=500,KI=0,KD=0.响应曲线如图 3:
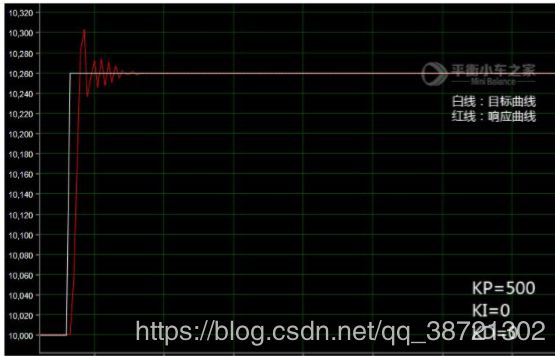
这个时候因为 P 值比较大,出现了震荡。可能大家会疑惑,为什么 I 值为零,但是没有静差呢?因为这个时候的 P 值已经很大了,静差一般是在 P 值较小而 I值为零的时候出现的。为了验证我们的想法,我们对 PID 参数进行调整。
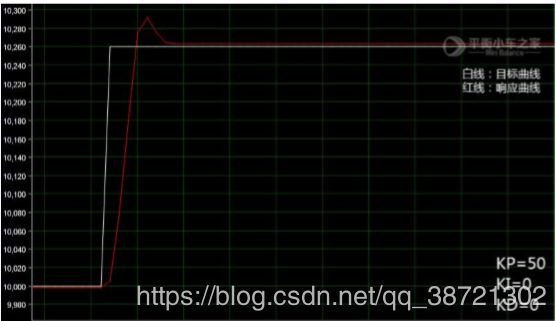
② KP=50,KI=0,KD=0.响应曲线如图 4:
据图分析,如我们所设想的,在 P 值较小的时候出现了静差,响应速度也明显降低。所以增大 P 值可以一定程度上消除静差,提高响应速度,但是会导致系统震荡,而加入微分控制可以有效抑制震荡。下面我们尝试一组新的 PID 参数
③ KP=500,KI=0,KD=400.响应曲线如图 5
据图分析,加入微分控制之后,图 5 与图 3 相比,系统的震荡得到了抑制,震荡次数减少。事物都有两面性,微分控制也是弊端的。可以看到,系统的响应明显变慢了,因为引入微分控制相当于增大了系统的阻尼。这个时候我们需要结合 P
值和 I 值进行进一步的优化。
在实践生产工程中,不同的控制系统对控制器效果的要求不一样。比如平衡车、倒立摆对系统的快速性要求很高,响应太慢会导致系统失控。智能家居里面的门窗自动开合系统,对快速性要求就不高,但是对稳定性和准确性的要求就很高,所以需要严格控制系统的超调量和静差。所以 PID 参数在不同的控制系统中是不一样的。只要我们理解了每个 PID 参数的作用,我们就可以应对工程中的各
种项目的 PID 参数整定了。
位置控制的调节经验可以总结为:先只使用 P 控制,增大 P 系数至系统震荡之后加入微分控制以增大阻尼,消除震荡之后再根据系统对响应和静差等的具体要求,调节 P 和 I 参数。
一般而言,一个控制系统的控制难度,一般取决于系统的转动惯量和对响应速度的要求等。转动惯量越小、对响应速度要求越低,PID 参数就越不敏感。
在我们的小车上面定的数据是
float Position_KP=40,Position_KI=0.1,Position_KD=200;2.速度闭环控制
速度闭环控制就是根据单位时间获取的脉冲数(这里使用了 M 法测速)测量电机的速度信息,并与目标值进行比较,得到控制偏差,然后通过对偏差的比例、积分、微分进行控制,使偏差趋向于零的过程。一些 PID 的要点在位置控制中已经有讲解,这里不再赘叙。需要说明的是,这里速度控制 20ms 一次,一般建议 10ms 或者 5ms,因为在这里电机是使用 USB 供电,速度比较慢,20ms 可以延长获取速度的单位时间,提高编码器的采值。
2.1 理论分析
根据增量式离散 PID 公式
在我们的速度控制闭环系统里面只使用 PI 控制,因此对 PID 控制器可简化为以下公式
float Velocity_KP=5,Velocity_KI=5; //PID系数/**************************************************************************
函数功能:增量PI控制器
入口参数:编码器测量值,目标速度
返回 值:电机PWM
根据增量式离散PID公式
pwm+=Kp[e(k)-e(k-1)]+Ki*e(k)+Kd[e(k)-2e(k-1)+e(k-2)]
e(k)代表本次偏差
e(k-1)代表上一次的偏差 以此类推
pwm代表增量输出
在我们的速度控制闭环系统里面,只使用PI控制
pwm+=Kp[e(k)-e(k-1)]+Ki*e(k)
**************************************************************************/
int Incremental_PI (int Encoder,int Target)
{
static float Bias,Pwm,Last_bias;
Bias=Encoder-Target; //计算偏差
Pwm+=Velocity_KP*(Bias-Last_bias)+Velocity_KI*Bias; //增量式PI控制器
Last_bias=Bias; //保存上一次偏差
return Pwm; //增量输出
}2.2 控制原理图
图 8 为速度控制原理图
(以上内容部分来源于送的开发指南,如有违规联系作者删除)