Restricted Boltzmann Machine（限制玻尔兹曼机 RBM）

RBM原理：

玻尔兹曼机最初是作为一种广义的“联结主义”引入，用来学习向量上的任意概率分布。联结主义（connectionism）的中心思想是，当网络将大量简单计算单元连接在一起时可以实现智能的行为。分布式表示（distributed representation）认为系统每个输入应该由许多特征表示的，并且每个特征应参与多个可能输入的表示。
特别在不是所有变量都能被观察到时，具有隐藏单元的玻尔兹曼机不再局限于线性关系会十分强大，用处在于学习一组数据的“内在表示”，因此可以看到它没有输出层的概念。其实玻尔兹曼机也很符合大脑神经的工作，比如连接两个随机变量的轴突和树突只能通过观察他们物理上实际接触的细胞的激发模式来学习，而且经常被同时激活的两个单元之间的连接会被加强。

玻尔兹曼机也是这样，如上图所示，RBM由两层浅层网络组成，一层是可视层 v，一层是隐藏层 h，相互之间是全连接。它与神经网络不同点就在于，RBM是生成学习方法，即学习输入数据的概率模型，是非监督学习，所以它在做完前向运算后，反向部分仍然是他自己，即相当于自动编码机的编码与解码重构的过程。除开推导我们要求的就是这其间的W，a，b等参数，使差距最小化。

此时假设所有的节点都是随机二值变量节点（只能取0或1，这是“限制”的来源，也代表了神经元状态，1代表该神经元处于接通状态，0代表该神经元处于断开状态），而且对于向量v，h假设全概率分布基于能量Boltzmann分布：
$$E(v,h)=-a^{T}v-b^{T}h-h^{T}Wv$$
其中a，b是偏倚系数，而W是权重矩阵。

为什么是0，1二分？
在生物学中，连接两个随机变量的轴突和树突只能通过观察与它们物理上实际接触的细胞的激发模式来学习。特
别地，正相期间，经常同时激活的两个单元之间的连接会被加强。这意味着对于权重的学习规则可以是 ‘‘局部’’ 的，这使得玻尔兹曼机的学习似乎在某种程度上是生物学合理的。
另外在下面的推导中，RBM这种二分图的设计会让概率的计算、参数的采样都会简单太多太多，效率和效果都非常棒！

为什么是“能量”？
首先可以为了对应物理学中，有关势能的概念，在统计学中x经常是成对出现的，也很适合RBM模型。
而RBM的能量函数的意思就是，每个可视节点和隐藏节点之间的连接结构之间都有一个能量，通过v和h之间的往来参数的学习，我们可以计算出它的能量。通过能量这一概念可以捕获变量之间的相关性，而变量之间的相关程度决定了能量的高低。在统计力学上的说法也是——能量低的状态比能量高的状态发生的概率高。另外神经网络的变化过程，实质是一个能量不断减少的过程，最终达到能量的极小值点，也就是稳态。

且有能量函数，v,h的联合概率分布为：
$$P(v,h)=\frac{1}{Z}{e}^{-E(v,h)}$$
其中Z是被称为配分函数的归一化常数（可以类比softmax）：
$$Z=\sum _{v,h}{e}^{-E(v,h)}$$
这里必须对这一概率图模型使用归一化，即除去配分函数Z，才能得到有效的可供训练的概率分布，但是！由于配分函数Z的难以处理，又提出了一些挑战。那么既然无法直接求解，最好用的方法莫过于近似了。在这里使用最大似然梯度来近似。
首先从联合分布中导出条件分布：
$$P(h|v)=\frac{P(h,v)}{P(v)}=\frac{1}{P(v)}\frac{1}{Z}exp\{a^{T}v+b^{T}h+h^{T}Wv\}$$
为了推导方便将无关值（比如在求h|v的时候，v，以及与它有关的a是可知的）统一变成 Z’ 表示，然后可以有：
$$\begin{gathered} P(h|v)=\frac{1}{Z^{\prime }}exp\{b^{T}h+h^{T}Wv\}=\frac{1}{Z^{\prime }}exp\{\sum _{j=1}^{n_h}(b_j^T{h}_j+h_j^T{W}_{:,j}{v}_j)\} \\ =\frac{1}{Z^{\prime }}\prod _{j=1}^{n_h}exp\{b_j^T{h}_j+h_j^T{W}_{:,j}{v}_j\} \end{gathered}$$
可以容易的得到在给定可视层v的基础上，隐层第j个节点为1或者为0，即每个节点为“on”和“off”状态的概率为：
$$\begin{gathered} P(h_j=1|v)=\frac{P(h_j=1|v)}{P(h_j=1|v)+P(h_j=0|v)} \\ =\frac{exp\{b_j+W_{:,j}{v}_j\}}{exp\{0\}+exp\{b_j+W_{:,j}{v}_j\}} \\ =\frac{1}{1+exp\{-(b_j+W_{:,j}{v}_j)\}} \\ =sigmoid(b_j+W_{:,j}{v}_j) \end{gathered}$$
可以看到就是相当于使用了sigmoid激活函数！同样的在给定h也可以推得有关v的分布，即现在同样可以写出关于隐藏层的完全条件分布：
$$P(v_j=1|h)=sigmoid(a_j+W_{:,j}{h}_j)$$
基于此重新再回到v和h的联合分布，为了求出参数W，a，b，可以先定义RBM的对数损失函数并使其最小化：$$L(W,a,b)=-\sum _{i=1}^{m}ln(P(v，h{)}^{(i)})$$
对于某个单个样本P，$$-ln(P(v，h))=-ln(\frac{1}{Z}\sum _h{e}^{-E(V,h)})=lnZ-ln(\sum _h{e}^{-E(V,h)})=ln(\sum _{v,h}{e}^{-E(v,h)})-ln(\sum _h{e}^{-E(V,h)})$$
然后如果对a求导可得：
$$\frac{\partial (-ln(P(v，h)))}{\partial a_i}=\frac{1}{\partial a_i}\partial ln(\sum _{v,h}{e}^{-E(v,h)})-\frac{1}{\partial a_i}\partial ln(\sum _h{e}^{-E(v,h)})$$$$=-\frac{1}{\sum _{v,h}{e}^{-E(v,h)}}\sum _{v,h}{e}^{-E(v,h)}\frac{\partial E(v,h)}{\partial a_i}+\frac{1}{\sum _h{e}^{-E(v,h)}}\sum _h{e}^{-E(v,h)}\frac{\partial E(v,h)}{\partial a_i}$$$$=\sum _{h}P(h|V)\frac{\partial E(v,h)}{\partial a_i}-\sum _{v,h}P(h,v)\frac{\partial E(v,h)}{\partial a_i}=-\sum _{h}P(h|v，h)v_i+\sum _{v,h}P(h,v)v_i$$$$=-\sum _{h}P(h|v，h)V_i+\sum _{v}P(v)\sum _{h}P(h|v)v_i=\sum _{v}P(v)v_i-V_i$$
同理对b和W：
$$\frac{\partial (-ln(P(v)))}{\partial b_i}=\sum _{v}P(v)P(h_i=1|v)-P(h_i=1|v)$$
$$\frac{\partial (-ln(P(v)))}{\partial W_{ij}}=\sum _{v}P(v)P(h_i=1|v)v_j-P(h_i=1|v)v_j$$

推导了这么久，其实RBM就是可以被看做是一个自编码器。从可见层到隐藏层的输入样本，W，a然后用Sigmoid激活得到0，1值的过程就是编码，只有0，1的限制会让整个模型更简单，更易训练和理解。而从隐藏层到可见层的神经元值和W，b的过程就是解码，然后优化期望差距尽可能小，迭代最后得到模型。然后通过解码过程可以对测试集进行预测。

梯度下降计算量太大？
那就近似。那就采样。
可以采用基于MCMC(Markov Chain Monte Carlo and **Gibbs Sampling**的方法来模拟计算求解每个样本的梯度损失再求梯度和。而Gibbs的作用是用来估计负梯度似然函数和在训练完模型之后进行采样，来看模型对数据的拟合以及网络中间隐含层的抽象效果。

wake-sleep方法。
1.wake：从下到上驱动神经元, 相邻层的神经元的二进制状态则可以被用来训练生成权值。
2.sleep：上到下的生成连接则被用来驱动网络, 从而基于生成模型(generative model)产生预测。

用RBM做minst数据：
RBM对minist里面一些噪音大，通过编码和解码，对于不清晰的图片能够有很好的学习。

import numpy
import cPickle
import gzip
import os
from utils import *

class RBM(object):
  def __init__(self, input=None, n_visible=28*28, n_hidden=500, \
      W=None, hbias=None, vbias=None, numpy_rng=None):

    self.input = input
    self.n_visible = n_visible
    self.n_hidden = n_hidden

    if numpy_rng is None:
      numpy_rng = numpy.random.RandomState(1234)#随机数生成numpy-rng
      
	#参数为none后，初始化为 -4*sqrt(6./(n_visible+n_hidden))
    if W is None：
      W = numpy.asarray(numpy_rng.uniform(
        low=-4 * numpy.sqrt(6. / (n_hidden + n_visible)),
        high=4 * numpy.sqrt(6. / (n_hidden + n_visible)),
        size=(n_visible, n_hidden)))

    if hbias is None:
      hbias = numpy.zeros(n_hidden)#偏置项都设为0

    if vbias is None:
      vbias = numpy.zeros(n_visible)

    self.numpy_rng = numpy_rng
    self.W = W
    self.hbias = hbias
    self.vbias = vbias

  def propup(self, vis):#前向
    pre_sigmoid_activation = numpy.dot(vis, self.W) + self.hbias
    return sigmoid(pre_sigmoid_activation)

  def sample_h_given_v(self, v0_sample):#根据可视层v采样计算隐层h为1的状态
    h1_mean = self.propup(v0_sample)
    h1_sample = self.numpy_rng.binomial(size=h1_mean.shape, n=1, p=h1_mean)#只有0和1两种状态
    return [h1_mean, h1_sample]

  def propdown(self, hid):#后向
    pre_sigmoid_activation = numpy.dot(hid, self.W.T) + self.vbias
    return sigmoid(pre_sigmoid_activation)

  def sample_v_given_h(self, h0_sample):#根据隐层v采样计算可视层
    v1_mean = self.propdown(h0_sample)
    v1_sample = self.numpy_rng.binomial(size=v1_mean.shape, n=1, p=v1_mean)
    return [v1_mean, v1_sample]

  def gibbs_hvh(self, h0_sample):#整个Gibbs采样
    v1_mean, v1_sample = self.sample_v_given_h(h0_sample)#v-h
    h1_mean, h1_sample = self.sample_h_given_v(v1_sample)#h-v
    return [v1_mean, v1_sample,
            h1_mean, h1_sample]

  def get_cost_updates(self, lr=0.1, persistent=None, k=1):#k为采样次数
    ph_mean, ph_sample = self.sample_h_given_v(self.input)#先根据输入input计算隐层的结果

    if persistent is None:
      chain_start = ph_sample
    else:
      chain_start = persistent

    for step in xrange(k):#计算k次
      if step == 0:
        nv_means, nv_samples,\
        nh_means, nh_samples = self.gibbs_hvh(chain_start)#拿到最后一次结束的状态
      else:
        nv_means, nv_samples,\
        nh_means, nh_samples = self.gibbs_hvh(nh_samples)

    self.W += lr * (numpy.dot(self.input.T, ph_mean)
                    - numpy.dot(nv_samples.T, nh_means))
    self.vbias += lr * numpy.mean(self.input - nv_samples, axis=0)
    self.hbias += lr * numpy.mean(ph_mean - nh_means, axis=0)

    monitoring_cost = numpy.mean(numpy.square(self.input - nv_means))#损失函数
    return monitoring_cost
    

def load_data(dataset='mnist.pkl.gz'):
  dataset = os.path.join(os.path.split(__file__)[0], '../data', dataset)
  f = gzip.open(dataset, 'rb')
  train_set, valid_set, test_set = cPickle.load(f)
  f.close()

  def make_numpy_array(data_xy):
    data_x, data_y = data_xy
    return numpy.array(data_x), numpy.array(data_y)

  train_set_x, train_set_y = make_numpy_array(train_set)
  valid_set_x, valid_set_y = make_numpy_array(valid_set)
  test_set_x, test_set_y = make_numpy_array(test_set)

  rval = [(train_set_x, train_set_y), (valid_set_x, valid_set_y),
          (test_set_x, test_set_y)]

  return rval
  
def test(learning_rate=0.1, k=1, training_epochs=15):
  datasets = load_data('mnist.pkl.gz')#载入minst数据
  train_set_x, train_set_y = datasets[0]
  test_set_x, test_set_y = datasets[2]

  rbm = RBM(input=train_set_x, n_visible=28 * 28, n_hidden=500)

  start_time = time.clock()

  for epoch in xrange(training_epochs):
    cost = rbm.get_cost_updates(lr=learning_rate, k=k)
    print ('Training epoch %d, cost is ' % epoch, cost)

  end_time = time.clock()
  pretraining_time = (end_time - start_time)

  print ('Training took %f minutes' % (pretraining_time / 60.))

if __name__ == '__main__':
  test()

RBM的作用？
一是对数据进行编码，然后交给监督学习方法去进行分类或回归。即把它当做一个降维的方法来使用。

二是得到了权重矩阵和偏移量，供 BP 神经网络初始化训练。即把它当作是一个预训练方法，原因就是神经网络也是要训练一个权重矩阵和偏移量，但是如果直接用 BP 神经网络，初始值选得不好的话，往往会陷入局部极小值，此时加入一个预训练的初始化方法，在实际效果中非常好。

三是，由于RBM 可以估计可视层和隐藏层的联合概率 p(v,h)，那如果把 v 当做训练样本，h 当成类别标签（隐藏节点只有一个的情况，能得到一个隐藏节点取值为 1 的概率），就可以利用利用贝叶斯公式求 p(h|v)，然后就可以进行分类，类似朴素贝叶斯、LDA、HMM。即RBM 可以作为一个生成模型（Generative model）使用，在自编码机中，变分自编码也是一个可以找出自己规律的生成模型。

四是，RBM 可以直接计算条件概率 p(h|v)，那如果把 v 当做训练样本，h 当成类别标签（隐藏节点只有一个的情况，能得到一个隐藏节点取值为 1 的概率），RBM 就可以用来进行分类，即RBM 可以作为一个判别模型（Discriminative model）使用。

加深层数！

加深RBM的层数后，可以变成Deep Boltzmann Machine（DBM）。由多个RBM和BP堆积而成，即它能做到的第二个用途。


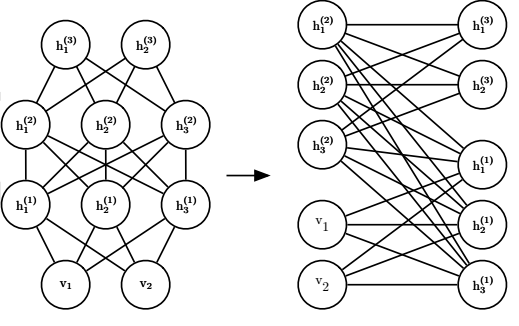
如上图的DBM，层内无连接，只有层间加强。
此时联合概率变为：$$P(v,h^{(1)},h^{(2)},h^{(3)})=\frac{1}{Z(\theta )}{e}^{-E(v,h^{(1)},h^{(2)},h^{(3)};\theta )}$$
能量函数变为：
$$E(v,h^{(1)},h^{(2)},h^{(3)};\theta )=-v^T{W}^{(1)}{h}^{(1)}-h^{(1{)}^T}{W}^{(2)}{h}^{(2)}-h^{(2{)}^T}{W}^{(3)}{h}^{(3)}$$
与RBM的能量函数相比，DBM能量函数包括权重矩阵 ($W^{(2)}$ 和 $W^{(3)})$ 形式的隐藏单元（潜变量）之间的连接。

但是其实对于全相连玻尔兹曼来说，DBM也可以变成一个“限制”的二分图，奇数一侧，偶数一侧，这就反而使得DBM能更加的高效，特别是在使用MCMC进行采样的时候，当然这种形态也更容易变形和处理。根据不同的应用场景，RBMs在类似 协同滤波、分类、降维、图像检索、信息检索、语言处理、自动语音识别等等方面都有很好的效果。

主要参考：
bengio deep learning