（CNN）卷积神经网络（三）-理解卷积操作

第一篇文章介绍了卷积神经网络的数据输入形式和权值的初始化：CNN）卷积神经网络（一）
第二篇文章介绍了卷积操作，常用的激活函数（CNN）卷积神经网络（二
下面来看一下接下来的层级结构：

1-池化层（pooling layer）

由第一张图可以看到池化层压在卷积层中；因为做完卷积操作之后，还是有很大的数据量级，为了减少参数的数量，降低计算机资源消耗，同时缓解过拟合，通常会抽取大部分重要的数据出来，用来表征整张图片，而其他的就会去掉。其实这么做就是为了保留有效的数据（信息）。
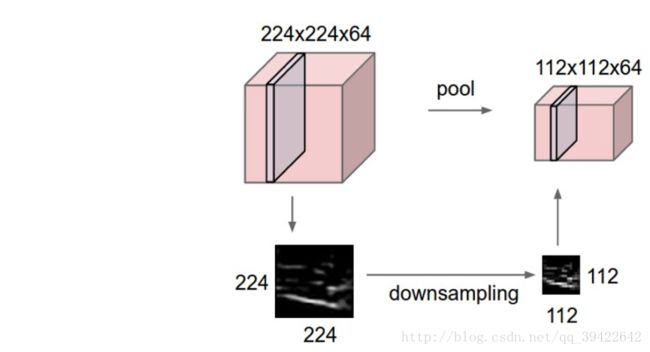如图，昨晚下采样之后，图片数据的维度就从224X224X64降为112X112X64了。

那pooling layer 具体是怎么实现的呢？
为了保留图片的大部分信息，一般会采用max操作，也就是在2X2的区域内的四个数，取最大值。

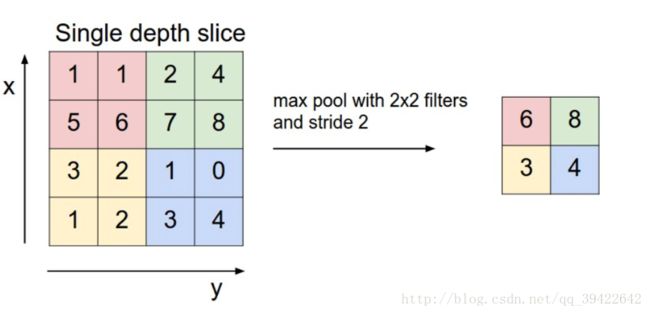
另一个操作就是取average，求这2X2的区域的平均值嘛！

2- FC（全连接层）

两层之间都有权重连接，通常全连接层在卷积神经网络的尾部。
主要是因为如果下采样层采样的太猛了，可以通过这一层进行重新拟合出来。
这一层并不是一定要的，但也有把全连接层拿掉的，比如Googlenet.

最经典的卷积神经网络是：

输入层⇒[[卷积层→激励层]∗N（若干个）→池化层]∗M⇒[FC→RELU]∗K⇒FC

3-可视化理解

第一个卷积层
左边的filter，右边是昨晚卷积操作之后得到的。

你会发现，不同的神经元关注的点不一样，有的是关注它的轮廓，有的是关注它的形状，有的是关注它的颜色，最后每个filter得到的结果合起来就是这个卷积层对整张图片的理解了。

• 举个小栗子，就像一堆人同时看一个美女一样，有的人关注胸，都有的人关注腿，有的人关注眼睛，有的关注头发，然后把所有人对于这个美女的关注点都综合起来，就可以画出这个美女大概是什么样子的。

第二个卷积层
这是第二个卷积层

貌似我们已经不明白它到底是在干嘛了，但卷积神经网络就是通过这样的操作，最终有了图像识别的能力。

4- CNN的训练算法

同一般的机器学习一样，卷积神经网络也是先定义损失函数，来衡量预测出来的和实际结果之间的差别，最小化损失函数中W和b，CNN用的优化算法是SGD，这个SGD默认分批的，CNN也用BP算法来求偏导，值得一提的是，在下采样层的偏导该怎么求呢？

下采样的函数如果采用max的话，函数可以表示为:

max(x1,x2,x3,…,xn)

因为这个函数是分段函数，所以求导数也是分段求的，假如 x3 是最大值，那就可以得到 [0,0,1,…,0] 的向量表示。
在此不详细说了，这个还是比较麻烦的。

说一下它的优点

• 对高维的数据处理无压力，因为有共享卷积核
• 不用手动抽取特征，训练好权重后，就可以得到特征
• 深层次的网络抽取图像信息丰富，表达的效果也很好

缺点

• 卷积神经网络乃至其他的神经网络，都有一个大问题，就是没有具体的物理含义在，里面做了什么不知道，就像一个黑箱。
• 需要调参数，和非常大的数据量来训练，GPU是必须的

5-从数学的角度理解卷积

前面说了卷积神经网络没有具体的物理含义，但在数学上，很早就有卷积的定义了,所以我想从数学这个角度，给大家提供一个理解卷积的思路。

卷积和的定义如下：

离散型：y(t)=x(t)∗h(t)=∑τ=−∞∞x(τ)h(t−τ)(1)

连续型：x(t)∗h(t)=∫∞−∞x(τ)h(t−τ)dτ=∫∞−∞x(t−τ)h(τ)dτ(2)

第一种思路 ：降维打击

由公式（1），你会发现两个函数（ x(t),h(t) ）变成了一个函数： y(t) ,用数学术语表示就是把二元函数卷成一元函数了，俗称降维打击，可能这就是为什么卷积操作能减少参数量的原因之一吧。

第二种思路：傅立叶变换与卷积

卷积公式是从傅立叶变换推导出来的，所以从源头的角度来看一下，希望能有助于理解。
首先看一下傅立叶变换的一个推论：

[αf(t)+βg(t)]=αF(s)+βG(s)

傅立叶常用于信号处理，这个公式的含义就是：一个时域下的复杂信息函数可以分解成多个简单信号函数的和，然后对各个子信号函数做傅立叶变换并求和，就求出了原信号的傅立叶变换。

除了加法，还有乘法，这时候，有一个问题：是否存在一种新的结合方式，使得 f(t),g(t) 结合后的函数的傅立叶变换结果是 F(s)G(s) ？

我们用倒推法来试一下能不能推出这样的结合方式，假设有信号函数 f(x),g(t)（x,t 均为横轴自变量），F(s),G(s)分别为他们的傅立叶变换, 有：

G(s)F(s)=∫∞−∞e−2πistg(t)dt∫∞−∞e−2πisxf(x)dx

接着做一些变换：

∫∞−∞e−2πistg(t)dt∫∞−∞e−2πisxf(x)dx=∫∞−∞∫∞−∞e−2πiste−2πisxg(t)f(x)dtdx

=∫∞−∞∫∞−∞e−2πis(t+x)g(t)f(x)dtdx

=∫∞−∞(∫∞−∞e−2πis(t+x)g(t)dt)f(x)dx

现在设u = t + x，所以t = u - x，du = dt（这是把x看做常数项了）。则有：

∫∞−∞(∫∞−∞e−2πis(t+x)g(t)dt)f(x)dx=∫∞−∞(∫∞−∞e−2πisug(u−x)du)f(x)dx

接着调整下积分顺序：

∫∞−∞(∫∞−∞e−2πisug(u−x)du)f(x)dx=∫∞−∞∫∞−∞e−2πisug(u−x)f(x)dudx

=∫∞−∞∫∞−∞e−2πisug(u−x)f(x)dxdu

=∫∞−∞e−2πisu(∫∞−∞g(u−x)f(x)dx)du

括号内那个积分是一个关于u的函数，所以可以设成h(u)：

h(u)=∫∞−∞g(u−x)f(x)dx

于是上面的式子就变成:

∫∞−∞e−2πisu(∫∞−∞g(u−x)f(x)dx)du=∫∞−∞e−2πisuh(u)du=[h(s)]=H(s)

这个结论，可以简化成：

H(s)=G(s)F(s)

再来看下h(u)。如果把h(u)的u换成t（这是可以的，只是一个符号而已），就有:

h(t)=∫∞−∞g(t−x)f(x)dx

2个终极公式都出来了。

最后，我们还要定义一个特殊的二元运算符号∗∗来替代h(t)（也叫卷积运算符，注意，这个不是乘法的乘号哦）：

h(t)=(g∗f)(t)=∫∞−∞g(t−x)f(x)dx

于是有：

H(s)=G(s)F(s)

[h(t)]=[g(s)][f(s)]

[(g∗f)(s)]=[g(s)][f(s)]

最后的公式，也被叫做 卷积定理(Convolution Theorem)。

这个定理说明，信号f和信号g的卷积的傅里叶变换，等于f、g各自的傅里叶变换的积,因此，傅里叶变换将一个函数或是信号表示为许多弦波的叠加。

虽然公式很恼人，但是傅立叶变换在其中扮演的角色，相当于一种映射之类的，提供了一种信号间的连接关系。更直观得，快速傅立叶变换是一种将时域和空域中的数字转换到频域中的算法，如下所示，你可以看到一个信号是如何被傅立叶变换转换的：

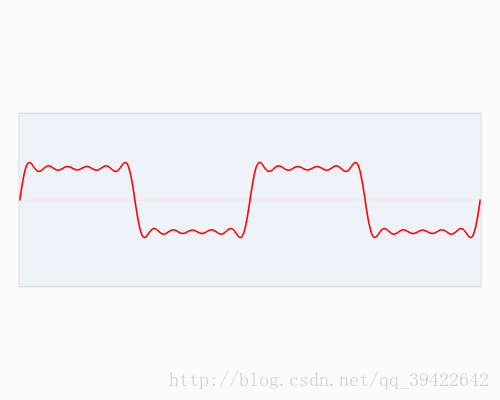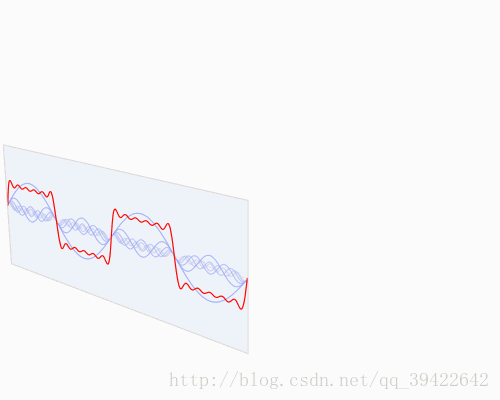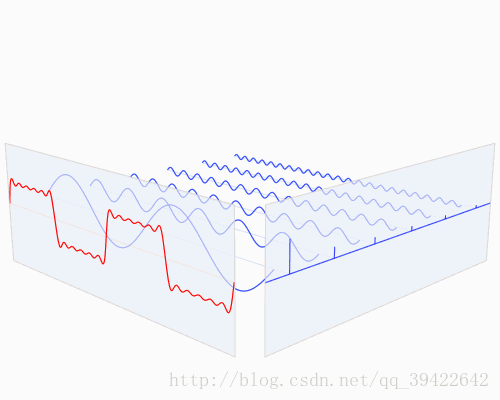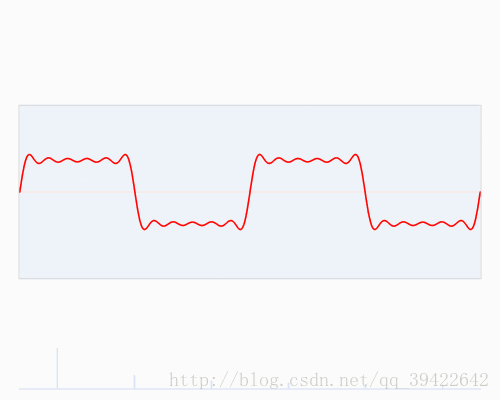
红色代表时域，蓝色代表频域。这在现实中又是什么呢？如果红色代表你听到的音乐的话，那么蓝色就代表这首音乐对应的频谱。
更加详细的关于傅立叶变换可以参考这篇文章： 如果看了这篇文章，还不懂傅立叶变换，那就过来掐死我