梯度下降法的matlab实现
NOTE:这是本人在学习NG课程后,尝试练习的用matlab实现的梯度下降算法。具体的梯度下降法的知识点不在赘述。
请参考线性回归 梯度下降知识点
一、线性回归(Linear Regression)
方法一利用公式 :(懂了)
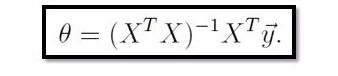
function [ theta ] = linearReg()
%线性回归。
X=[1 1;1 2;1 3;1 4]; %注意第一列全为1,即x0=1,第二列才为x1
Y=[1.1;2.2;2.7;3.8];
A=inv(X'*X);
theta=A*X'*Y; %根据公式theta=(X'*X)^(-1)*X'*Y;
end注释:
1.这种方法最简单,但是公式推导过程很复杂
2.inv() 求逆
3. X ’是求X的转置
方法二:使用梯度下降法迭代(代码不懂)
function theta=linearRegression()
% 梯度下降法寻找最合适的theta,使得J最小
options=optimset('GradObj','on','MaxIter',100);
inittheta=[1 1]';
theta=fminunc(@costFunc,inittheta,options);
end
%%
function [J,gradient]= costFunc(theta)
%J为代价函数。
%y=theta(0)*x0+theta(1)*x1; 找出最好的theta来拟合曲线。
%使得J最小的theta就是最好的theta
x=[1;2;3;4];
y=[1.1;2.2;2.7;3.8];
m=size(x,1);
hypothesis=theta(1)+theta(2)*x;
delta=hypothesis-y;
J=sum(delta.^2)/(2*m);
gradient(1)=sum(delta.*1)/m; %x0=1;
gradient(2)=sum(delta.*x)/m;
end注释:
1.Matlab中fminunc函数的意义 以及options函数的初级用法
2.
function theta=linearRegression()
% 梯度下降法寻找最合适的theta,使得J最小
options=optimset(‘GradObj’,’on’,’MaxIter’,100);
inittheta=[1 1]’;
theta=fminunc(@costFunc,inittheta,options);
end
结合注释1,这个目前看不懂,先记住,这是梯度下降算法的一个小套路吧!
3.这两种方法,都采用数据:
x=[1;2;3;4];
y=[1.1;2.2;2.7;3.8];
当然,用的时候可以换成其它数据,两种方法得出的结果都是
theta =
0.3000
0.8600即可以学习到线性函数:
Y=0.3000+0.8600*X;
补充:
第一个代码计算梯度下降(懂了)
clear all
clc
% training sample data;
p0=26;
p1=73;
x=1:3;
y=p0+p1*x;
num_sample=size(y,2);
% gradient descending process
% initial values of parameters
theta0=1;
theta1=3;
%learning rate
alpha=0.08;
% if alpha is too large, the final error will be much large.
% if alpha is too small, the convergence will be slow
epoch=500;
for k=1:epoch
v_k=k
h_theta_x=theta0+theta1*x; % hypothesis function
Jcost(k)=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2)/num_sample;
theta0=theta0-alpha*((h_theta_x(1)-y(1))+(h_theta_x(2)-y(2))+(h_theta_x(3)-y(3)))/num_sample;
theta1=theta1-alpha*((h_theta_x(1)-y(1))*x(1)+(h_theta_x(2)-y(2))*x(2)+(h_theta_x(3)-y(3))*x(3))/num_sample;
% disp('*********comp 1**************');
r1=((h_theta_x(1)-y(1))+(h_theta_x(2)-y(2))+(h_theta_x(3)-y(3)));
r2=sum(h_theta_x-y);
% disp('*********comp 2**************');
r3=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2);
r4=sum((h_theta_x-y).^2);
% disp('*********comp 3**************');
r5=((h_theta_x(1)-y(1))*x(1)+(h_theta_x(2)-y(2))*x(2)+(h_theta_x(3)-y(3))*x(3));
r6=sum((h_theta_x-y).*x);
if((r1~=r2)||(r3~=r4)||(r5~=r6))
disp('***wrong result******')
end
end
plot(Jcost)注释:
1.代码里面类似
r1=((h_theta_x(1)-y(1))+(h_theta_x(2)-y(2))+(h_theta_x(3)-y(3)));
r2=sum(h_theta_x-y);
想说明,r2和r1其实是一样的, r1是r2 的具体展开
2. if((r1~=r2)||(r3~=r4)||(r5~=r6))中
~=不等号
|| 或
第二个代码,对第一个代码进行简化(懂了)
clear all
clc
% training sample data;
p0=26;
p1=73;
x=1:3;
y=p0+p1*x;
num_sample=size(y,2);
% gradient descending process
% initial values of parameters
theta0=1;
theta1=3;
%learning rate
alpha=0.08;
% if alpha is too large, the final error will be much large.
% if alpha is too small, the convergence will be slow
epoch=500;
for k=1:epoch
v_k=k
h_theta_x=theta0+theta1*x; % hypothesis function
Jcost(k)=sum((h_theta_x-y).^2)/num_sample;
%替代了原来的 {Jcost(k)=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2)/num_sample;} 下面的做了类似的简化,可以参考上面理解 。
r0=sum(h_theta_x-y);
theta0=theta0-alpha*r0/num_sample;
r1=sum((h_theta_x-y).*x);
theta1=theta1-alpha*r1/num_sample;
end
plot(Jcost)
第三个代码多变量梯度下降的线性回归(懂了)
备注:多变量一定要进行均值归一
%三个个输入变量x1、x2和x3.
clear all
clc
% training sample data;
p0=6;
p1=7;
p2=2;
p3=9;
x1=[7 9 12 5 4];
x2=[1 8 21 3 5];
x3=[3 2 11 4 8];
x1_mean=mean(x1)
x1_max=max(x1)
x1_min=min(x1)
x1=(x1-x1_mean)/(x1_max-x1_min)
x2_mean=mean(x2)
x2_max=max(x2)
x2_min=min(x2)
x2=(x2-x2_mean)/(x2_max-x2_min)
x3_mean=mean(x3)
x3_max=max(x3)
x3_min=min(x3)
x3=(x3-x3_mean)/(x3_max-x3_min)
y=p0+p1*x1+p2*x2+p3*x3;
num_sample=size(y,2);
% gradient descending process
% initial values of parameters
theta0=9;
theta1=3;
theta2=9;
theta3=2;
% theta0=19;theta1=23;theta2=91;
% theta0=0;theta1=0;theta2=0;
%learning rate
alpha=1.8; % good for the system
% alpha=0.01; % good for the system
% alpha=0.02; % bad for the system. the system will be unstable
% if alpha is too large, the final error will be much large.
% if alpha is too small, the convergence will be slow
epoch=2260;
for k=1:epoch
v_k=k
h_theta_x=theta0+theta1*x1+theta2*x2+theta3*x3; % hypothesis function
Jcost(k)=sum((h_theta_x-y).^2)/num_sample;
r0=sum(h_theta_x-y);
theta0=theta0-alpha*r0/num_sample;
r1=sum((h_theta_x-y).*x1);
theta1=theta1-alpha*r1/num_sample;
r2=sum((h_theta_x-y).*x2);
theta2=theta2-alpha*r2/num_sample;
r3=sum((h_theta_x-y).*x3);
theta3=theta3-alpha*r3/num_sample;
end
yt=theta0+theta1*x1+theta2*x2+theta3*x3
plot(Jcost)第四NG作业中梯度下降代码的实现
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters) %定义梯度下降函数
m = length(y); %训练实例的个数
for iter = 1:num_iters
H = X * theta;%假设函数向量化
T = [0 ; 0];%给T赋了初值
for i = 1 : m,
T = T + (H(i) - y(i)) * X(i,:)';
end
theta = theta - (alpha * T) / m;
J_history(iter) = computeCost(X, y, theta);
end
end注释:
1.实际上T=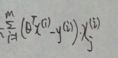
经过向量推导后(推导过程见3)第i行,第j列,T=![]()
故 for i = 1 : m,
T = T + (H(i) - y(i)) * X(i,:)’;
end
这个for循环实际就是实现了对上图式子的求和
2.参数theat的向量化表示如下图

故
3.推导过程
![]()
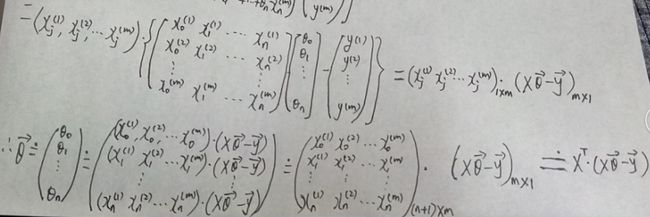
4. theta = theta - (alpha * T) / m;
实际上就是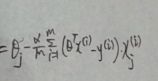
.实际上T=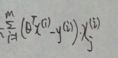
经过向量推导后(推导过程见3)第i行,第j列,T=![]()
5. J_history(iter) = computeCost(X, y, theta);
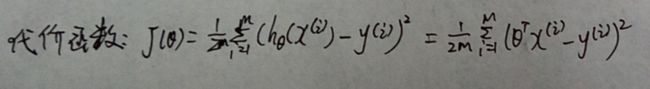
j= sum((X*theta - y).^2) / (2 * m);
6.具体细节先理解到这,慢慢理解不着急,慢慢向前走,一定可以成功!