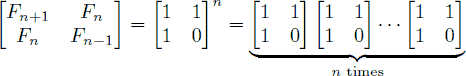UESTC278 Fibonacci（矩阵快速幂，模运算，模板，斐波那契）

In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

Given an integer n, your goal is to compute the last 4 digits of Fn.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of Fn. If the last four digits of Fnare all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).

Sample Input

0
9
999999999
1000000000
-1

Sample Output

0
34
626
6875

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

.

Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

.

 

初学矩阵快速幂，简单讲一下，参考B站

其实快速幂核心思想很简单，就是拆分

例如a^10=a^8*a^2，10的二进制是1010 ，即1*2^3+0*2^2+2^1+0*2^0

其他的矩阵快速幂，或者模运算都很简单，都是这个思想的展开

这个题基本上都包含了，首先斐波那契数列用了矩阵，结果也要模运算，快速幂肯定要用到

看代码中的几个经典模板

import java.util.Scanner;

import java.util.Arrays;

class mat{
    int[][] a=new int[2][2];//矩阵该矩阵存储菲波那切数列的方式是
/*
    f(n+1)  f(n)
    f(n)    f(n-1)
*/
    mat(){
        for(int i=0;i<2;i++)
            Arrays.fill(a[i], 0);//初始化
    }
}
public class Main {
    static mat I=new mat();
    
    static mat matrax(mat q,mat p){//矩阵运算模板，还包括了模运算
        mat e = new mat();

        for(int i=0;i<2;i++)
            for(int j=0;j<2;j++){
                for(int k=0;k<2;k++){
                    e.a[i][j]+=(q.a[i][k]*p.a[k][j])%10000;
                }
                e.a[i][j]%=10000;//注意这里还要模一次，参考模运算的运算律
            }
        return e;
    }
    
    static mat quicklymod(mat b,int n){//快速幂模板求取矩阵b^n
        mat ans=new mat();

        ans.a=I.a;单位矩阵初始化，就和求数a^n,初始赋值1相同，单位矩阵*任何矩阵不改变
        while(n>0){
            if((n&1)==1) ans=matrax(b,ans);//与运算最后一位是不是1，如果是，则ans*b,此时b为初始b的2的某个次方，就是拆分
            
            b=matrax(b,b);//进位，幂次+1
            n>>=1;//进位，右移一位
        }
        return ans;
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Scanner sc=new Scanner(System.in);
        
        I.a[0][0]=I.a[1][1]=1;
        I.a[0][1]=I.a[1][0]=0;//初始化单位矩阵
        
        int n;
        n=sc.nextInt();
        while(n!=-1){
            mat b=new mat();
            b.a[0][0]=1;b.a[0][1]=1;
            b.a[1][0]=1;b.a[1][1]=0;//初始化菲波那切数列矩阵你
            /*
                f(2)  f(1)
                f(1)  f(0)
            */
            if(n<=2){
                if(n==0) System.out.println("0");
                else if(n==1) System.out.println("1");
                else if(n==2) System.out.println("1");
            }else{                
                b=quicklymod(b,n);//求取矩阵b^n
                System.out.println(b.a[0][1]);
            }        
            n=sc.nextInt();
        }
    }

}