机器学习:sklearn分类报告classification_report()中精确率, 召回率, F1等的含义
一、classification_report简介
def classification_report(y_true, y_pred, labels=None, target_names=None, sample_weight=None, digits=2, output_dict=False)
print(classification_report(testY, predictions))该函数就是在进行了分类任务之后通过输入原始真实数据(y_true)和预测数据(y_pred)而得到的分类报告,常常用来观察模型的好坏,如利用f1-score进行评判
它的输出是类似下面这样的(该输出结果为对mnist手写数字的分类,共有10类):
precision recall f1-score support
0 1.00 1.00 1.00 44
1 0.94 0.98 0.96 48
2 0.98 0.98 0.98 44
3 1.00 0.89 0.94 44
4 0.92 1.00 0.96 56
5 0.93 0.96 0.95 57
6 0.98 0.96 0.97 48
7 1.00 1.00 1.00 42
8 0.94 0.91 0.92 33
9 0.97 0.91 0.94 34
accuracy 0.96 450
macro avg 0.97 0.96 0.96 450
weighted avg 0.96 0.96 0.96 450二、各分类指标的含义
要想知道这些数据是怎么算出来的,要先了解一下几个常见的模型评价术语,现在假设我们的分类目标只有两类,计为正例或阳例(positive)和负例或阴例(negtive)分别是:
(1)True positives(TP): 被正确地划分为正例的个数,即实际为正例且被分类器划分为正例的实例数(样本数);
(2)False positives(FP): 被错误地划分为正例的个数,即实际为负例但被分类器划分为正例的实例数;
(3)False negatives(FN):被错误地划分为负例的个数,即实际为正例但被分类器划分为负例的实例数;
(4)True negatives(TN): 被正确地划分为负例的个数,即实际为负例且被分类器划分为负例的实例数。
| 实 际 类 别 |
预测类别 | |||
| 是 | 否 | 总计 | ||
| 是 | TP | FN | P(实际上为该类的) | |
| 否 | FP | TN | N(实际上不是该类的) | |
| P‘被分类器分为属于该类的 | N’被分类器分为不属于该类的 | P+N | ||
要注意P = TP + FN 而不是 TP+FP
1.精确率(precision)
precision = TP / ( TP + FP )
精确率是精确性的指标,表示被分类器正确分为正例的个数(TP)占被分类器分为正例的样本(TP+FP)的比重。
2.召回率(recall)
recall = TP / ( TP + FN ) = TP / P
召回率是覆盖面的度量,也就是被分类器正确分为正例的个数(TP)占原始数据中全部正例(TP+FN)的比重。
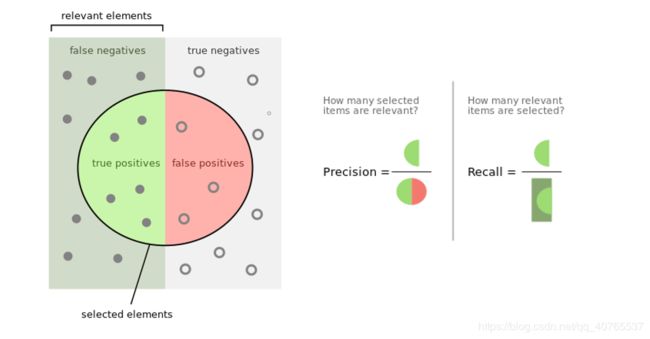
如果有些难理解,可以看一下下面这张图:
上面relevant elements 可以理解成属于该类的,右半部分就是不属于该类的,其中TP = 5 , FN = 7,FP = 3 ,TN = 7
所以 precision =TP / ( TP + FP ) = 5/(5+3) = 0.625
recall =TP / ( TP + FN )= 5/(5+7) = 0.417
3.F1 score
也称为F-beta score
只有当P和R都很高的时候,F1才会高,所以称为调和平均数,F1的取值范围是0到1
按照前面的数值 F1 = 0.50
4.support
支持度,是指原始的真实数据中属于该类的个数
5.accuracy
准确率,这个跟精确率只有一字之差,但实际上有很大的不同,它是指正确分类(不管是正确分为P还是N)的比率
accuray = (TP + TN) / (TP + FP + TN + FN ) = (TP + TN) / (P+N)
事实上从字面上看accuray和f1一样都可以作为一个指标评判整个模型,但是accruracy存在一个bug,当数据严重不均衡时, accuracy不起作用,比如我们看X光片,真实数据是:99%都是无病的,只有1%是有病的,假设一个分类器只要给它一张X 光片,它就判定是无病的,那么它的准确率也有99%,乍看很高,然而这个模型根本就不work。
6.宏平均(macro avg)和微平均(micro avg)
比如不同类别对于precision的宏平均是将各类的precision先算好再对它们求算术平均。
而对于precision的微平均是将所有类中中真阳例先加起来,再除以所有类中的(真阳例+假阳例)。下面是一个例子:
第一类
TP1= 12,FP1=9,FN1=3
Then precision (P1) and recall (R1) will be 57.14 and 80
第二类
TP2= 50,FP2=23 ,FN2=9
Then precision (P2) and recall (R2) will be 68.49 and 84.75
宏平均
Macro-average precision = (P1+P2)/2 = (57.14+68.49)/2 = 62.82
Macro-average recall = (R1+R2)/2 = (80+84.75)/2 = 82.25
微平均
Micro-average of precision = (TP1+TP2)/(TP1+TP2+FP1+FP2) = (12+50)/(12+50+9+23) = 65.96
Micro-average of recall = (TP1+TP2)/(TP1+TP2+FN1+FN2) = (12+50)/(12+50+3+9) = 83.78
微平均在classification_report中只有在多标签分类的时候才会显示,多标签不是指多个类,而是一个样本可能属于两个或以上的类。
7.加权平均(weighted avg)和样本平均(sample avg)
(1)加权平均(weighted avg):加上每个类的权重,即它的support的大小
精确度P的weighted avg = (P1 * support1 + P2 * support2) / (support1+support2)
(2)样本平均(sample avg):跟微平均一样,仅在多标签分类时显示
三、其他评判指标
(1)灵敏度(sensitive)
sensitive = TP/P,表示的是所有正例中被分对的比例,衡量了分类器对正例的识别能力,可以看到召回率与灵敏度是一样的。
(2)特效度(specificity)
specificity = TN/N,表示的是所有负例中被分对的比例,衡量了分类器对负例的识别能力;
参考资料:
https://en.wikipedia.org/wiki/Precision_and_recall
https://en.wikipedia.org/wiki/F1_score
https://www.cnblogs.com/mxp-neu/articles/5316989.html