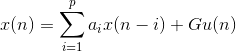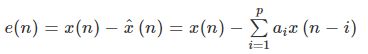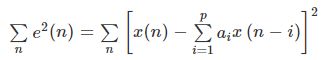自适应滤波器:线性预测理论(LPC)
本文转载自:http://www.cnblogs.com/xingshansi/p/6621914.html
前言
西蒙.赫金的《自适应滤波器原理》第四版第三章,线性预测是Wiener Filter的应用,作为信号识别的特征以及信号编码的一种实现途径。本想着跳过这一章,但想着每一章多少记录一下,直到看到Kalman Filter,也就写写吧。主要包括:
1)前向线性预测原理;
2)线性预测应用实例;
内容为自己的学习笔记,如有不当之处,希望各位帮忙指出!
一、前向线性预测原理
以语音信号为例,声道模型的一种观点是:级联结构的共振峰模型。即:对于一般元音,可以用全极点模型,传输函数:
G为幅值因子,p为极点个数。
这里仅仅讨论全极点模型。对于输出![]() 和激励
和激励![]() 有差分方程:
有差分方程:
称系统
为线性预测器。![]() 是
是![]() 的估算值。
的估算值。![]() 为预测系数(Linear Prediction Coefficient, LPC),p为对应阶数。
为预测系数(Linear Prediction Coefficient, LPC),p为对应阶数。
对应单点预测误差:
预测误差:
对![]() 求偏导即可实现求解,得出的方程组通常称为Yule-Walker方程。
求偏导即可实现求解,得出的方程组通常称为Yule-Walker方程。
二、应用实例
利用预测系数估计逼近系统响应H,可以用该系数表征语音的特性,也可以用逼近的H观察声道特性,同样可以进行共振峰提取,这些都可以看作说话人的特征。
给出代码:
clear all; clc; close all;
filedir=[]; % 设置数据文件的路径
filename='a.wav'; % 设置数据文件的名称
fle=[filedir filename] % 构成路径和文件名的字符串
[x,fs]=wavread(fle); % 读入语音数据
L=240; % 帧长
p=30; % LPC的阶数
y=x(8001:8000+L); % 取一帧数据
ar=lpc(y,p); % 线性预测变换
nfft=512; % FFT变换长度
W2=nfft/2;
m=1:W2+1; % 正频率部分下标值
Y=fft(y,nfft); % 计算信号y的FFT频谱
Y1=lpcar2ff(ar,W2-1); % 计算预测系数的频谱
% 作图
subplot 311; plot(y,'k');
title('一帧语音信号的波形'); ylabel('幅值'); xlabel('(a)')
subplot 312;
plot(m,20*log10(abs(Y(m))),'k','linewidth',1.5);
line(m,20*log10(abs(Y1)),'color','r','linewidth',2)
axis([0 W2+1 -30 25]); ylabel('幅值/db');
legend('FFT频谱','LPC谱',3); xlabel(['样点' 10 '(b)'])
title('FFT频谱和LPC谱的比较 p=4');
subplot 313;
plot(m,20*log10(abs(Y(m))),'k','linewidth',1.5);
line(m,20*log10(abs(Y1)),'color','r','linewidth',2)
axis([0 W2+1 -30 25]); ylabel('幅值/db');
legend('FFT频谱','LPC谱',3); xlabel(['样点' 10 '(c)'])
title('FFT频谱和LPC谱的比较 p=30');
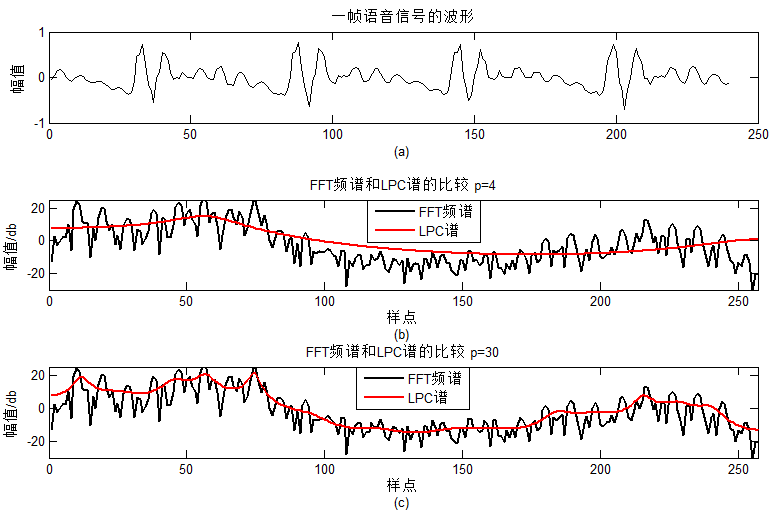
对应结果图:
可以看出,信号的频谱由慢变化分量调制高频信号,对应时域就是卷积,而声道模型对应卷积的h(n),p选择过小估计不准,选择过大容易过拟合,这么看来lpc说是预测其实本质也是拟合的问题,同样有Over-fitting. 得到LPC谱之后,可以利用峰值查找等方式,进行共振峰估计。
参考:
- Simon Haykin 《Adaptive Filter Theory Fourth Edition》.
- 宋知用:《MATLAB在语音信号分析和合成中的应用》.