GAN以及小样本数据扩增的一些论文笔记

• 1. 几种常见的GAN介绍
• • 1.1. 原始GAN
• • 1.2. CGAN
• • 1.3. Semi-Supervised GAN
• • 1.4. AC-GAN
• 2. Data Augmentation with Few Shot Learning
• • 2.1. SMOTE
• • 2.2. WGAN
• • 2.3. BAGAN

1. 几种常见的GAN介绍

1.1. 原始GAN

arxiv: https://arxiv.org/pdf/1406.2661.pdf

作为开山之作，Ian Goodfellow提出的GAN是最原始的模型()，其余都是在这个基础上所进行的变种。

GAN由两个网络组成，生成网络Generator和判别网络Discriminator。

• Generator负责接收随机的噪声z，通过这个噪声生成样本，记为G(z)；

• Discriminator判定生成的样本是不是真实的，接收输入x，输出D(x)代表x为真实样本的概率。

通过这样我们可以知道Generator的目标是尽量生成真实的样本去欺骗Discriminator，而Discriminator要尽可能区分出真实样本和虚假样本，二者构成了动态的博弈过程，用数学语言描述即为
$${\min }_G{\max }_{D}V(D,G)={\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathbb{E}}_{z\sim p_{data}(z)}[\log (1-D(G(z)))]$$
x表示的是真实的样本，z是输入Generator的噪声，这样G(z)便是Generator生成的样本。D(x)是判断真实样本是否为真的概率，而因为x就是真实的，对于D来说，这个值越接近1越好。而D(G(z))则是判断G生成的样本是否为真的概率。对于G而言，它希望D(G(z))越大越好，这样会使得V(D,G)变小；而对于D而言，它希望D(x)越大越好，D(G(z))越小越好，这样就使得结果会变大。其最后的结果是G生成以假乱真的样本，而D没有办法判断它是否为真，因此D(G(z))=0.5。它的代码流程如图1所示。

图1

1.2. CGAN

axiv: https://arxiv.org/pdf/1411.1784.pdf

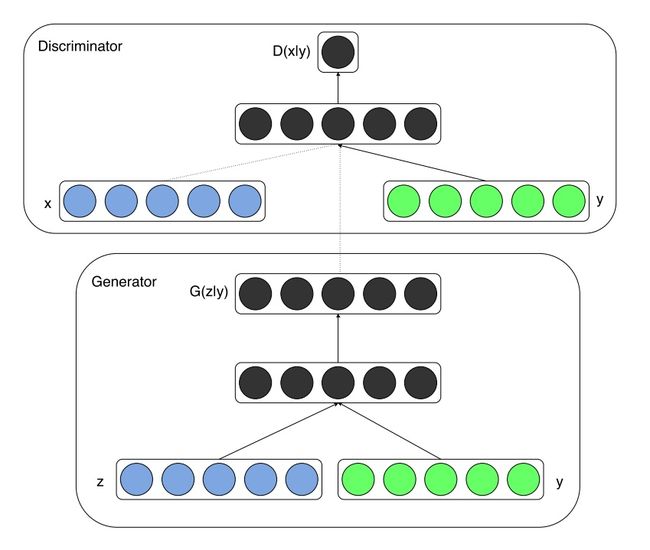
相比较原始的GAN，CGAN(Conditional GAN)对生成的样本数据增设了模式上的控制，它对模型增加了额外的条件信息，使得数据生成过程在一定的引领下运作，这样的额外信息可以是类标签，可以是如在图像修复中的一部分数据，或者是不同模态的数据。
CGAN的结构如图2所示。

图2 可以看到其结构与原始GAN差别并不大，区别在于CGAN中y也作为Generator和Discriminator的输入，那么它的目标函数就变为：

$${\min }_G{\max }_{D}V(D,G)={\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x\mid y)]+{\mathbb{E}}_{z\sim p_{data}(z)}[\log (1-D(G(z\mid y)))]$$

1.3. Semi-Supervised GAN

arxiv: https://arxiv.org/pdf/1606.01583.pdf

尽管CGAN在训练时增加了类标签使得我们可以输出特定的样本类型，它的判别网络的输出还是和原始GAN一样，仅是一个判断生成样本是否为真的0-1概率输出。而在半监督GAN中，Discriminator有N+1个输出，其中N是样本的分类数。该方法可以训练出一个更有效的分类器，同时也能生成具有更高质量的样本。该工作在原先的模型上的改进是，将前向网络的末端的sigmoid输出改成了softmax层，因而D网络拥有了N+1维的输出，也就起到了分类的作用。

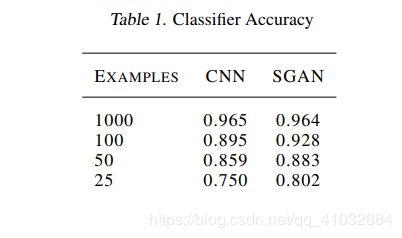
在MNIST实验来看SGAN是否比一般GAN得到更好的生成样本，如图3所示，SCAN（左）的输出要比GAN（右）的输出更为清晰，这看起来对于不同的初始化和网络架构都是正确的，但很难对不同的超参进行样本质量的系统评估。

图3 在分类效果上，SGAN也展现了非常好的效果，为了训练基线，在这一部分没有更新Generator。图4显示SGAN的性能超过了baseline，而且越缩减训练集，效果越为明显，这表明令判别器和分类器共享权重提高了数据效率。

图4

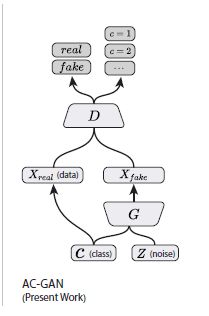
1.4. AC-GAN

arxiv: https://arxiv.org/pdf/1610.09585.pdf
ACGAN的全称为Auxiliary Classifier Generative Adversarial Network（带辅助分类器的GAN），它和其它几个gan网络的结构如图5所示：

图5 我们可以看到，和CGAN直接将类标签输入到判别器不同，ACGAN认为判别器有能力自动识别类标签，这通过在判别器中加入一个输出训练集或者生成样本的潜在变量子集的类标签的辅助解码网络来实现。 它的loss函数有两个，分别为判别损失和分类损失：

$$L_S=E[\log P(S=real\mid X_{real})]+E[\log P(S=fake\mid X_{fake})]$$
$$L_C=E[\log P(C=c\mid X_{real})]+E[\log P(C=c\mid X_{fake})]$$

D期望得到最大化的$L_S+L_C$，而G则期望最大化$L_C-L_S$。从结构上看，该模型与其它现有模型并没有太大区别，然而其修改产生了非常好的效果，展现出稳定的训练性能。ACGAN的结构也允许将大型数据集依照分类拆分成小子集来训练判别器和生成器。

2. Data Augmentation with Few Shot Learning

我们都知道，在现有的深度学习技术框架下，训练数据规模越大，标注质量越高，算法模型性能就越好，标注数据对深度学习的应用效果有决定性的作用。然而在许多应用场景中，标注样本获取困难且成本高，亦或者是数据的高维性和复杂性也阻碍了数据获取。这些问题使得传统统计机器学习算法无法获得好的泛化性能，也制约了深度学习的应用。

当特征空间的维度大于样本数量，我们认为这种情况属于小样本学习[Theodordis S,et al.]。

传统的解决标注样本不足问题的方法主要是过采样技术。早期通过简单复制原始数据集或者在数据集上加入人工噪声形成新数据集来解决数据不平衡情况下标注样本不足的问题[1]。2002年，Chawla等人[2]提出了经典的合成少数类过采样技术(synthetic minority oversampling technique,SMOTE)并生成模拟样本；Han等人[3]基于SMOTE方法提出了边界和距离边界合成少数类过采样技术。这两种方法都是考虑了相邻的样本并过采样处于边界附近的样本。

2.1. SMOTE

arxiv: https://arxiv.org/pdf/1106.1813.pdf

相比起旋转、倾斜等常用的传统上采样方法在“数据空间”的操作，SMOTE方法更倾向于一种在特征空间的操作，而这是一个更广泛而不受应用限制的方法。通过提取每个少数类的样本并从与该点最近的k个同类近邻的连线中得到多个合成的样本，根据采样的要求，我们从k个近邻中也会随机的选择近邻进行合成。一般来说k取值为5，而如果我们要求过采样率为200%，那么将随机从五个近邻中选取2个然后生成样本。而合成样本是这样生成的：从特征向量与近邻中计算距离并将距离与范围在0-1之间的随机数相乘，得到的结果再与特征向量相加。实验结果表明了SMOTE算法可以少数类样本分类的准确率，是一种非常经典的解决数据不平衡问题的算法。但在实际应用中，数据集还可能面临的问题不仅是数据不平衡，还有每类样本规模均较小，难以对模型进行有效训练的问题。

2.2. WGAN

arxiv: https://arxiv.org/pdf/1701.04862.pdf
arxiv: https://arxiv.org/pdf/1701.07875.pdf
WGAN全称为沃瑟斯坦生成对抗网络，它与原始GAN的不同在于在评估真实样本和生成样本之间分布差异的时候它用Wasserstein距离替代了JS(Jensen-Shannon)差异来评估，这使得训练速度变得更快，训练过程趋于稳定（这一直是原始GAN的弊端）。

作者用两篇论文，推了一堆公式，分析了原始GAN的问题所在，并且针对性地给出了改进要点，最后给出了最终的算法流程，而其对原始GAN的改进实际上只是改进了四点：

• 判别器最后一层去掉sigmoid
• 生成器和判别器的取值都不取log
• 每次更新判别器参数后把绝对值截断，限制其不超过固定常数c
• 不用动量的优化算法（momentum和Adam），推荐RMSProp和SGD
  伪代码如图6所示：
  

图6

2.3 BAGAN

arxiv: https://arxiv.org/pdf/1803.09655.pdf

由IBM推出的BAGAN（Balancing GAN）是在ACGAN上进行了一定的改进，解决了不平衡数据集中样本数量少的问题。
图7是BAGAN的网络结构：

图7 我们再重新回顾一下ACGAN的网络结构：

ACGAN

我们可以看到，ACGAN有两个输出，如果我们用于小样本类别生成的时候，两个loss会出现矛盾。当一个判别器接收数据，它会本能将出现次数很少的数据认定为假样本，迫使生成器减少其输出，那这样它就会多输出数量多的类别数据，那我们就没法生成需要的小样本类别数据了。

这篇文章主要解决了两个问题：一是样本数量少的时候如何训练，它采用了自编码器，这样
就可以从小样本和其他样本之间学到共同特征，来避免小样本数据学习到的特征不足导致网络训练不好；第二个是修改ACGAN网络，将输出由两个变为一个，解决两个损失函数自相矛盾的问题。

原文在MNIST，CIFAR-10和交通标识等数据集上进行了实验。给出的实验结果在数据增强上效果做的很不错。

[1]DeRouin E,Brown J. Neural network training on unequally represented　 classes. New York: ASME Press; 1991.

[2]Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. SMOTE: synthetic minority over-sampling technique. J Artif Intell Res 2002;16(1):321-57.

[3]Han H, Wang WY, Mao BH. Borderline-SMOTE: a new over-sampling method　 in imbalanced data sets learning. In: Huang DS, Zhang XP, Huang GB, editors. Advances in intelligent computing. Berlin: Springer 2005. p. 878-87.