统计学习方法 第三章习题解答
文章目录
- 习题3.1
- 习题3.2
- 习题3.3
- 参考
习题3.1
题目:参照图3.1,在二维空间中给出实例点,画出k为1和2时的k近邻法构成的空间划分,并对其进行比较,体会k值选择与模型复杂度及预测准确率的关系。
答:本题的意思我理解蛮久(汗-_-||),简单来讲,将一整块的空间分割成各个区域,每个区域有其标签类别。书中的图(如下)给出的是最近邻也就是k=1的特征空间划分。
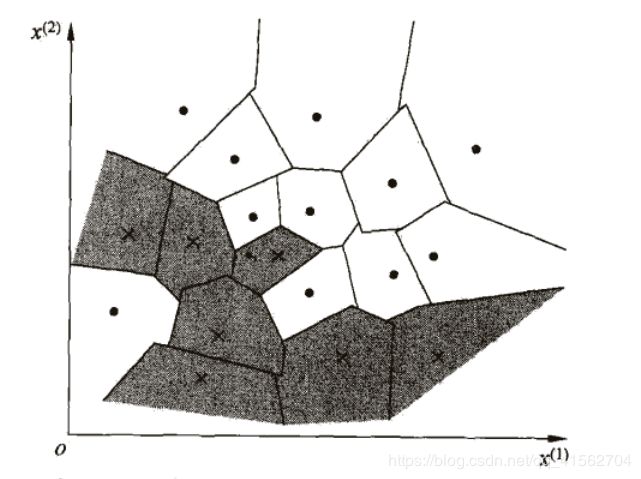
接下来我详细地解释一下如何划分(小学数学):
为了方便说明,只用两种类别,分别用○和×代表。
假设空间上只有两个点,要把整个空间一分为二,分成两个区域,我们知道要取两点的线段的中垂线来划分整个区域。同理多个点也是一样的。
K=1
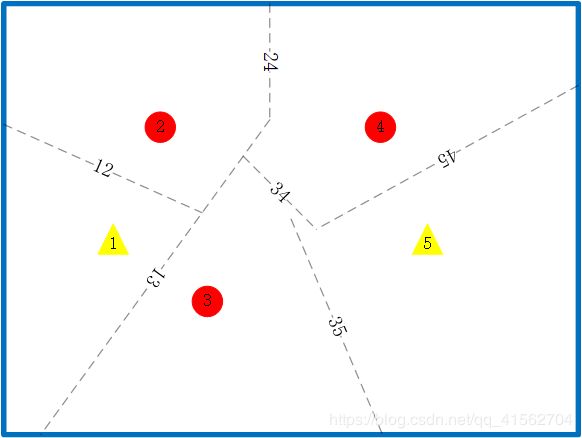
解释:每条线的标签表示哪两个点之间中垂线,整个空间由6条中垂线划分为5个区域
K=2
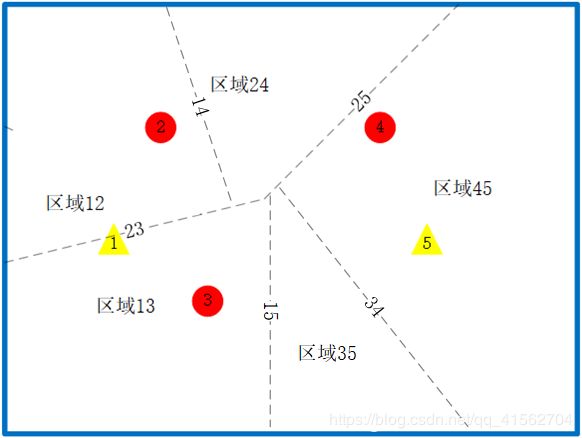
单单从结果图看可能有点抽象了,区域12的意思表示该区域最近的两个点是1和2。建议自己画一下点之间的中垂线,找一找感觉。(上图还有点小问题,应该还有区域23,比较小)
以区域13为例,要保证这个区域最近的两个点为1和3,那么从2点开始考虑,2靠1更近,要在该区域选择3而不是2,作出23的中垂线;同时要在该区域选择1而不是5,作15的中垂线。简言之作某个区域的时候,对剩余的点进行遍历,作该点与区域中距离该点较远的点之间的中垂线。
习题3.2
题目:利用例题3.2构造的kd树求点 x = ( 3 , 4.5 ) T x = (3,4.5)^T x=(3,4.5)T的最近邻点。
距离用欧式距离来衡量,即 d 2 = ( x a ( 1 ) − x b ( 1 ) ) 2 + ( x a ( 2 ) − x b ( 2 ) ) 2 d^2 = (x^{(1)}_{a}-x^{(1)}_{b})^2+(x^{(2)}_{a}-x^{(2)}_{b})^2 d2=(xa(1)−xb(1))2+(xa(2)−xb(2))2
答:例题3.2的特征空间划分和构造出的kd树如图所示:
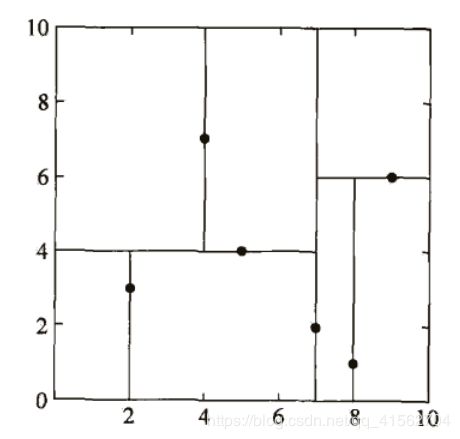
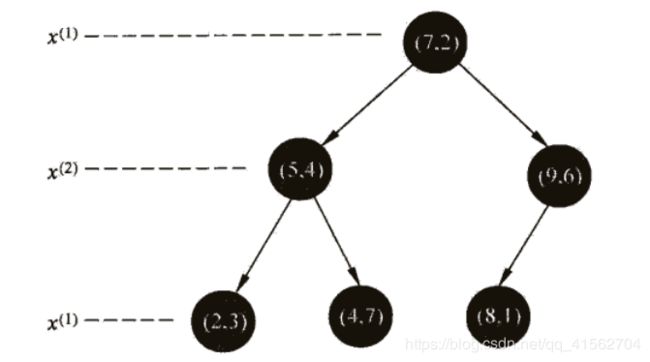
第一步:在kd树中找到包含目标点x的叶节点
从根节点 ( 7 , 2 ) (7,2) (7,2)开始, x = ( 3 , 4.5 ) T x = (3,4.5)^T x=(3,4.5)T的 x ( 1 ) < 7 x^{(1)} < 7 x(1)<7,进入左节点 ( 5 , 4 ) (5,4) (5,4),而 x ( 2 ) > 4 x^{(2)} > 4 x(2)>4进入右节点 ( 4 , 7 ) (4,7) (4,7),目标节点 x x x在叶节点 ( 4 , 7 ) (4,7) (4,7)对应的区域中,这一点也可以观察图1特征空间的划分得出来, x x x在左上角的矩形区域中。
第二步:递归向上退,更新“当前最近点”
比较
① d d d(当前节点,目标节点)与 d d d(当前最近点,目标节点)
② d m i n d_{min} dmin(当前节点的兄弟节点,目标节点)与 d d d(当前最近点,目标节点)
| 迭代次数 | 当前节点 | 兄弟节点中最近的节点 | 当前最近点 | 是否更新 |
|---|---|---|---|---|
| 0 | ( 4 , 7 ) (4,7) (4,7) | - | ( 4 , 7 ) (4,7) (4,7) | - |
| 1 | ( 4 , 7 ) (4,7) (4,7) | ( 2 , 3 ) (2,3) (2,3) | ( 4 , 7 ) (4,7) (4,7) | Yes |
| 2 | ( 5 , 4 ) (5,4) (5,4) | ( 5 , 4 ) (5,4) (5,4) | ( 2 , 3 ) (2,3) (2,3) | No |
| 3 | ( 7 , 2 ) (7,2) (7,2) | - | ( 2 , 3 ) (2,3) (2,3) | - |
第三步:退回到根节点时,“当前最近点”即为最近邻点
最终 ( 2 , 3 ) (2,3) (2,3)为要求的最近邻点。
代码实现
import numpy as np
class kdNode():
def __init__(self, x, y):
self.value = x
self.dimension = y #切分的x维度
self.left = None
self.right = None
def loadData():
T = np.array([[2,3], [5,4], [9,6], [4,7], [8,1], [7,2]])
return T
def buildTree(T, Depth):
if len(T) == 0:
return None
k = T.shape[1]
T = T[T[:, int(Depth % k)].argsort()]
mid = T.shape[0] // 2
root = kdNode(T[mid], Depth%k)
root.left = buildTree(T[:mid], Depth+1)
root.right = buildTree(T[mid+1:], Depth+1)
return root
def levelTravel(root):
queue = [root]
level = 0
while len(queue):
temp = []
print("第%d层结点:"%level)
level += 1
for i in range(len(queue)):
print(queue[i].value)
if queue[i].left != None:
temp.append(queue[i].left)
if queue[i].right != None:
temp.append(queue[i].right)
queue = temp
def find_closest(root, x, min_dis, closest_point):
#step1:在kd树中找出包含目标点x的叶节点
if root == None:
return
#更新最短距离和最近点
cur_distance = (sum((root.value[:] - x)**2))**0.5
if min_dis[0] < 0 or cur_distance < min_dis:
min_dis[0] = cur_distance
for i in range(len(root.value)):
closest_point[i] = root.value[i]
# 递归向下访问kd树
if x[root.dimension] <= root.value[root.dimension]:
find_closest(root.left, x, min_dis, closest_point)
else:
find_closest(root.right, x, min_dis, closest_point)
#计算测试点和分割超平面的距离,如果相交则进入叶节点的右子树进行遍历查找最近点
distance = abs(x[root.dimension] - root.value[root.dimension])
if distance > min_dis[0]:
return
else:
if x[root.dimension] <= root.value[root.dimension]:
find_closest(root.right, x, min_dis, closest_point)
else:
find_closest(root.left, x, min_dis, closest_point)
return
if __name__ == "__main__":
T = loadData()
root = buildTree(T, 0)
levelTravel(root)
test_x = [3, 4.5]
closet_point = np.copy(root.value)
min_dis = np.array([-1.0])
find_closest(root, test_x, min_dis, closet_point)
print("测试的点", test_x)
print("最近的点",closet_point)
print("最短距离%f" % min_dis[0])
运行结果
第0层结点:
[7 2]
第1层结点:
[5 4]
[9 6]
第2层结点:
[2 3]
[4 7]
[8 1]
测试的点 [3, 4.5]
最近的点 [2 3]
最短距离1.802776
习题3.3
题目:参照算法3.3,写出输出为x的k近邻的算法。
算法3.3——用kd树求最近邻
输入:已构造的kd树;目标点x;
输出:x的最近邻.
(1)在kd树中找出包含目标点x的叶结点:从根结点出发,递归地向下访问
kd树.若目标点x当前维的坐标小于切分点的坐标,则移动到左子结点,否则移动到右子结点.直到子结点为叶结点为止.
(2)以此叶结点为“当前最近点”。
(3)递归地向上回退,在每个结点进行以下操作:
(a)如果该结点保存的实例点比当前最近点距离目标点更近,则以该实例点为“当前最近点”。
(b)当前最近点一定存在于该结点一个子结点对应的区域.检查该子结点的父结点的另一子结点对应的区域是否有更近的点.具体地,检查另一子结点对应的区域是否与以目标点为球心、以目标点与“当前最近点”间的距离为半径的超球体相交.
如果相交,可能在另一个子结点对应的区域内存在距目标点更近的点,移动到另一个子结点.接着,递归地进行最近邻搜索;
如果不相交,向上回退.
(4)当回退到根结点时,搜索结束.最后的“当前最近点”即为x的最近邻点
思路:设置一个prior_queue,排序标准为与输入点x的距离,每次更新“当前最近点”的时候,在队列长度不足k的时候,直接压入该节点,长度超过k且新点到x的距离比队列最后一个点到x的距离短的时候,则弹出末尾节点,压入新节点。但是这种思路可能导致最终队列不足k个,此时则需要回溯访问另一半树中的节点.
参考
kd树的算法实现原理及开源代码
k近邻详解
kd树从最近邻到k近邻(C++实现)