《A Baseline for 3D Multi-Object Tracking》论文笔记
论文名称:《A Baseline for 3D Multi-Object Tracking》(AB3DT)
论文地址:https://arxiv.org/pdf/1907.03961.pdf
Github项目地址:https://github.com/xinshuoweng/AB3DMOT
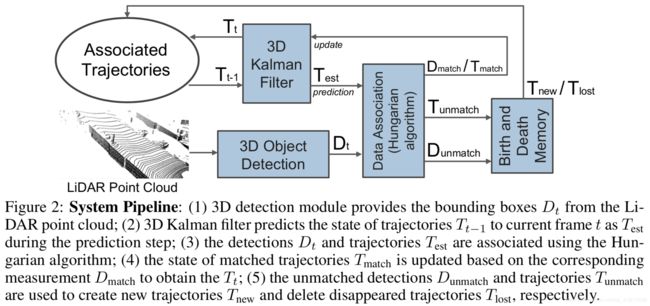
这是一篇CMU还在提交过程中的论文,代码已经开源。在我看来这就是一个3D版本的SORT算法,都用最简原则,组合了一些常规方法,构造了一个简单、精确、实时的3D MOT系统。它最强悍之处就是精度高且速度非常快!只需要CPU,不需要训练直接使用!(除了detector需要单独的预训练)。流程图总结一下就是这么简单,使用的是现成的3D detector,不过将卡尔曼滤波的状态空间拓展到3维算是一个创新。
![]()
摘要:
- real-time:近期3D MOT方向的论文都专注于通过更复杂的系统设计来达到更高精度,却不怎么重视计算负担和速度。但在实际应用中,速度是非常重要的衡量指标。这篇论文提出的3D MOT模型速度一骑绝尘,达到 215.7FPS,比SOTA的2D MOT模型要快65倍。
- SOTA:不仅速度快,它的模型性能也很好。在KITTI数据集中,它在3D评价指标(本论文提出的)上达到SOTA;将3D结果投影到2D后,在KITTI标准2D评价指标上位列第二。
- 将卡尔曼滤波的状态空间从2D拓展到3D。
- 3D MOT评价指标优化:将官方KITTI 2D MOT的评价指标拓展到3D,并提出了两个新的准则AMOTA/AMOTP。KITTI-3DMOT evaluation tool 已经开源。
文章目录
- 1 Introduction
- 2 Related Works
- 3 Approach
- 3.1 3D Object Detection
- 3.2 3D Kalman Filter —– State Prediction
- 3.3 Data Association
- 3.4 3D Kalman Filter —– State Update
- 3.5 Birth and Death Memory
- 4 New MOT Evaluation Tool
- 5 Experiment
- 5.1 Experiment Results
- 5.2 Ablation Study
1 Introduction
先来感受一下这个模型的威力:
没错,右上角的红点就是AB3DMOT,本文提出的模型。保持高精度的前提下,速度远超其它算法。其它一些特点和贡献在上面摘要中都有提及,不再赘述。
2 Related Works
2D MOT
| 类型 | 匹配问题建模 | 算法 |
|---|---|---|
| batch | 网络流图 | 最小费用流 |
| online | 二部图 | 匈牙利算法 / 深度匹配神经网络 |
本模型属于online模型,为了简单高速,采用原始匈牙利算法,并且只使用最简单的运动估计模型(匀速),不使用外观模型。
3D MOT
大部分3D MOT系统和2D MOT系统的模型框架是一致的,只不过是检测框从2D变成了3D。这使得我们可以利用3D空间中的信息来对运动模型、外观模型进行建模,不会受透视变形的影响。简单起见,我们的模型只使用了原始卡尔曼滤波,但将状态空间拓展到三维,包括3D速度、3D大小、3D位置以及目标的朝向角度。
3D Object Detection
和2D MOT一样,检测质量可以很大程度上影响整个追踪的质量。本论文中,我们用两个不同的检测器,分别进行实验。结果可见后面的对照实验。
之前有不少论文都关注于基于雷达点云进行3D bbox的检测:
PointRCNN: 3D Object Proposal Generation and Detection from Point Cloud. CVPR, 2019.
实验
Real Time End-to-End 3D Detection, Tracking and Motion Forecasting with a Single Convolutional Net. CVPR, 2018.
End-to-End Learning for Point Cloud Based 3D Object Detection. CVPR, 2018.
HDNET: Exploiting HD Maps for 3D Object Detection. CoRL, 2018.
当然也有直接基于单张图片进行3D检测的论文:
Monocular 3D Object Detection with Pseudo-LiDAR Point Cloud. 2019
实验
Monocular 3D Object Detection Leveraging Accurate Proposals and Shape Reconstruction. CVPR, 2019.
3 Approach
- 检测当前帧的3D bbox
- 3D卡尔曼滤波器 通过前一帧的目标状态 预测 当前帧的目标状态
- 用匈牙利算法对检测结果和目标预测状态进行匹配
- 用匹配上的检测结果去更新目标状态
- 没有被匹配上的检测结果将用于生成新目标,没有匹配上的目标预测状态将被删除
3.1 3D Object Detection
我们直接使用现成的3D detector,它们的原理请自行学习相应论文。
对于每一帧 t t t,3D detector的输出应该是一系列检测结果 D t = { D t 1 , D t 2 , ⋯ , D t n t } D_{t}=\left\{D_{t}^{1}, D_{t}^{2}, \cdots, D_{t}^{n_{t}}\right\} Dt={Dt1,Dt2,⋯,Dtnt},其中 n t n_t nt是检测到的物体的数量,在不同帧很可能是不同的值。每一个检测结果 D t i D_t^i Dti是一个八元组信息 ( x , y , z , l , w , h , θ , s ) (x, y, z, l, w, h, \theta, s) (x,y,z,l,w,h,θ,s)。其中 ( x , y , z ) (x,y,z) (x,y,z)是物体中心的三维坐标, ( l , w , h ) (l,w,h) (l,w,h)是物体的长宽高尺寸, θ \theta θ是朝向角, s s s是置信度。
3.2 3D Kalman Filter —– State Prediction
采用匀速模型,独立于相机的自身运动。
我们将目标轨迹状态建模为10维的向量 T = ( x , y , z , θ , l , w , h , v x , v y , v z ) T=\left(x, y, z, \theta, l, w, h, v_{x}, v_{y}, v_{z}\right) T=(x,y,z,θ,l,w,h,vx,vy,vz),其中 v x , v y , v z v_{x}, v_{y}, v_{z} vx,vy,vz分别代表目标在3D空间的速度。这里没有 v θ v_\theta vθ是因为我们在实际实验中发现添加它反而会带来负面影响。
在每一帧 t t t,我们对前一帧的所有目标轨迹状态 T t − 1 = { T t − 1 1 , T t − 1 2 , ⋯ , T t − 1 m t − 1 } T_{t-1}=\left\{T_{t-1}^{1}, T_{t-1}^{2}, \cdots, T_{t-1}^{m_{t-1}}\right\} Tt−1={Tt−11,Tt−12,⋯,Tt−1mt−1}进行前向预测,得到当前帧的预测位置:
x e s t = x + v x y e s t = y + v y z e s t = z + v z x_{\mathrm{est}}=x+v_{x} \quad y_{\mathrm{est}}=y+v_{y} \quad z_{\mathrm{est}}=z+v_{z} xest=x+vxyest=y+vyzest=z+vz
遵循匀速模型,目标轨迹状态在当前帧被相应预测为
T e s t j = ( x e s t , y e s t , z e s t , θ , l , w , h , v x , v y , v z ) T_{\mathrm{est}}^{j}=\left(x_{\mathrm{est}}, y_{\mathrm{est}}, z_{\mathrm{est}}, \theta, l, w, h, v_{x}, v_{y}, v_{z}\right) Testj=(xest,yest,zest,θ,l,w,h,vx,vy,vz)
这个预测状态将被用于接下来的匹配。
3.3 Data Association
detections和state predictions之间的相似度矩阵 ( n t × m t − 1 ) (n_{t} \times m_{t-1}) (nt×mt−1),用3D IoU来计算。然后用匈牙利算法解决二部图的最佳匹配问题。此外,还设置了一个阈值IoUmin,低于该阈值的匹配将被拒绝。
匹配步骤的输出是:
一系列匹配上的检测 D m a t c h = { D m a t c h 1 , D m a t c h 2 , ⋯ , D m a t c h w t } D_{\mathrm{match}}=\left\{D_{\mathrm{match}}^{1}, D_{\mathrm{match}}^{2}, \cdots, D_{\mathrm{match}}^{w_{t}}\right\} Dmatch={Dmatch1,Dmatch2,⋯,Dmatchwt}和对应的预测状态 T m a t c h = { T m a t c h 1 , T m a t c h 2 , ⋯ , T m a t c h w t } T_{\mathrm{match}}=\left\{T_{\mathrm{match}}^{1}, T_{\mathrm{match}}^{2}, \cdots, T_{\mathrm{match}}^{w_{t}}\right\} Tmatch={Tmatch1,Tmatch2,⋯,Tmatchwt},
以及没有被匹配上的预测状态 T unmatch = { T unmatch 1 , T unmatch 2 , ⋯ , T unmatch m t − 1 − w t } T_{\text {unmatch }}=\left\{T_{\text {unmatch }}^{1}, T_{\text {unmatch }}^{2}, \cdots, T_{\text {unmatch }}^{m_{t-1}-w_{t}}\right\} Tunmatch ={Tunmatch 1,Tunmatch 2,⋯,Tunmatch mt−1−wt}和检测 D unmatch = { D match 1 , D match 2 , ⋯ , D match n t − w t } D_{\text {unmatch }}=\left\{D_{\text {match }}^{1}, D_{\text {match }}^{2}, \cdots, D_{\text {match }}^{n_{t}-w_{t}}\right\} Dunmatch ={Dmatch 1,Dmatch 2,⋯,Dmatch nt−wt}
3.4 3D Kalman Filter —– State Update
我们用匹配上的检测 D m a t c h D_{\mathrm{match}} Dmatch更新对应轨迹预测状态 T m a t c h T_{\mathrm{match}} Tmatch,得到最终第 t t t帧的匹配轨迹 T t = { T t 1 , T t 2 , ⋯ , T t w t } T_{t}=\left\{T_{t}^{1}, T_{t}^{2}, \cdots, T_{t}^{w_{t}}\right\} Tt={Tt1,Tt2,⋯,Ttwt}。更新方式就是标准卡尔曼滤波,不清楚的话可以参考这篇博文。
不过我们对朝向角进行了特殊修正。我们指导根据卡尔曼滤波,最终更新的轨迹 T t i = ( x ′ , y ′ , z ′ , θ ′ , l ′ , w ′ , h ′ , v x ′ , v y ′ , v z ′ ) T_{t}^{i}=\left(x^{\prime}, y^{\prime}, z^{\prime}, \theta^{\prime}, l^{\prime}, w^{\prime}, h^{\prime}, v_{x}^{\prime}, v_{y}^{\prime}, v_{z}^{\prime}\right) Tti=(x′,y′,z′,θ′,l′,w′,h′,vx′,vy′,vz′)将是 D m a t c h D_{\mathrm{match}} Dmatch和 T m a t c h T_{\mathrm{match}} Tmatch的加权平均。但对于朝向而言,会出现一帧之内朝向出现完全反向的情况,这使得加权平均引入很大错误。这里,如果 D match i D_{\text {match }}^{i} Dmatch i和 T match i T_{\text {match }}^{i} Tmatch i的朝向角之差大于 π 2 \frac{\pi}{2} 2π,我们就在 T match i T_{\text {match }}^{i} Tmatch i的朝向角上加 π \pi π,使二者大致吻合。
3.5 Birth and Death Memory
我们考虑所有没被匹配上的detections都有可能是新出现的目标,但为了比避免追踪假正例,我们要求它能被连续检测 F m i n F_{min} Fmin帧,才真正生成新的轨迹 T new i T_{\text {new }}^{i} Tnew i(位置初始化为最近一帧的检测结果,速度初始化为0)。
另一方面,所有没有匹配上的轨迹都有可能是离开场景的物体,但为了避免删除真正例,我们将保持追踪 A g e m a x Age_{max} Agemax帧,在这段时间都没有匹配上,才会认为它消失。
4 New MOT Evaluation Tool
主要就是做了两件事:
- 将KITTI MOT的2D评价准则拓展到3D(2D IoU -> 3D IoU)
- 考虑了轨迹的置信度,提出AMOTA和AMOTP。其实就相当于目标检测中average precision(ap)的概念,它希望模型不是只在一个阈值表现好,而是在多个阈值下整体表现都不错。作者使用插值的方法来近似估计这个平均。
轨迹置信度被定义该轨迹在所有帧匹配的detection结果的置信度之平均。
5 Experiment
5.1 Experiment Results
5.2 Ablation Study
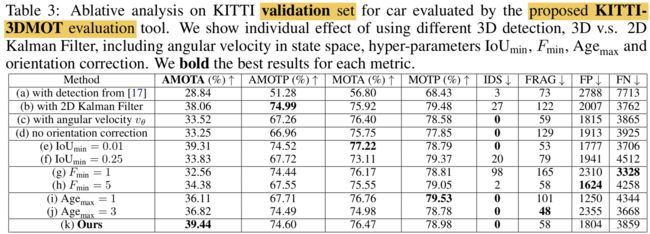
看到这里其实我有些疑惑,为什么这个简单的方法ID switch可以这么少,而且它只使用了运动特征,都没有使用外观特征来进行匹配。作者认为3D卡尔曼滤波的使用,使得我们可以用3D空间准确的depth信息来辅助匹配,因此比2D效果好。但是仔细看一下上图(b),即便使用2D卡尔曼滤波,IDS相比于其它方法也是非常小的。
其次,我们可以发现,如果换了一个检测器,即上图(a),这个模型性能显著下降。说明这个baseline的优秀性能基本依赖于优秀的3D检测器,本身的tracking架构有待商榷,完全可以进一步优化。