python 实现多元线性回归

一：一元线性回归
1.获取数据：数据库 postgre get_data

# -*- coding:utf-8 -*-
import psycopg2
import sys
# reload(sys)
# sys.setdefaultencoding('utf8')

# 获取数据
def get_data():
    conn = psycopg2.connect(host="xx", user="xx", password="xx", database="xx")
    cursor = conn.cursor()
    sql = 'SELECT dead_weight,liquid_capacity,draught,gross_tonnage,length_loa*mould_width area FROM shipxy_sample WHERE liquid_capacity !=0'
    cursor.execute(sql)
    # 获得数据
    DATA = cursor.fetchall()
    return DATA
    # 关闭指针和数据库
    cursor.close()
    conn.close()


if __name__ == "__main__":
    data =  get_data()
    print data
    for i in range(len(data)):
        # 获取第一列的数据
        print data[i][0]

2.通过求出相关系数来判断是否可以做线性回归：通过corr()方法

# 读取数据文件 第一列为y，后面的均为x
def read_data():
      # 通过read_csv来读取我们的目的数据集
      adv_data = pd.read_csv(u"xxx.csv")
      return adv_data

def correlation(data):
      ##相关系数矩阵 r(相关系数) = x和y的协方差/(x的标准差*y的标准差) == cov（x,y）/σx*σy
      # 相关系数0~0.3弱相关0.3~0.6中等程度相关0.6~1强相关
      print(data.corr()[data.columns[0]])

# 调用
new_data = read_data()
correlation(new_data)

效果为：

由第一列为y故是1，后面两个x和y的相关性为0.9多 属于强相关，所以可以做回归分析

3.画散点看看走势：

# -*- coding:utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import matplotlib.dates as mdate
import numpy as np
import get_data
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import sys
# reload(sys)
# sys.setdefaultencoding('utf8')

# 画散点图 看关系
def show_scatter(x,y):
    plt.rcParams['figure.figsize'] = (18.0, 15.0)  # 设置figure_size尺寸
    plt.rcParams['image.interpolation'] = 'nearest'  # 设置 interpolation style
    plt.rcParams['image.cmap'] = 'gray'  # 设置 颜色 style
    # 解决中文乱码问题
    plt.rcParams['font.sans-serif'] = ['Simhei']

    fig, ax = plt.subplots()

    ax.scatter(x, y, c='#FF8355', s=100)
    ax.set_ylabel(u'xx', fontsize=25)  # y轴标签
    ax.set_xlabel(u'', fontsize=25)  # x轴标签
    ax.set_title(u'xx', fontsize=30)  # title
    fig.tight_layout()
    # 画网格
    ax = plt.gca()
    ax.xaxis.set_major_locator(plt.MultipleLocator(1000))
    ax.xaxis.set_minor_locator(plt.MultipleLocator(500))  # 设置x从坐标间隔 0.1

    ax.yaxis.set_major_locator(plt.MultipleLocator(2000.0))
    ax.yaxis.set_minor_locator(plt.MultipleLocator(1000))  # 设置y从坐标间隔 0.1
    # x轴的范围
    plt.xlim(1, 31000)
    # y轴的范围
    plt.ylim(0, 60000)
    plt.xticks(fontsize=20,rotation=90)
    plt.yticks(fontsize=20)
    ax.grid(which='major', axis='x', linewidth=1, linestyle='-', color='0.75')  # 由每个x主坐标出发对x主坐标画垂直于x轴的线段
    ax.grid(which='minor', axis='x', linewidth=0.3, linestyle='-', color='0.75')  # 由每个x主坐标出发对x主坐标

    ax.grid(which='major', axis='y', linewidth=1, linestyle='-', color='0.75')
    ax.grid(which='minor', axis='y', linewidth=0.3, linestyle='-', color='0.75')

    plt.show()

效果：

4.求出最佳拟合线：下载 sklearn包

# -*- coding:utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import matplotlib.dates as mdate
import numpy as np
import get_data
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import sys
# reload(sys)
# sys.setdefaultencoding('utf8')

# 回归模型训练
'''
回归模型训练 :求出最佳拟合线 画出走势图（网格）
参数解析：
x:x变量 自变量
y:y变量 因变量
x_name：x轴描述
y_name：y轴描述
title：标题
x_start：x轴范围开始值
x_end：x轴范围结束值
y_start：y轴范围开始值
y_end：y轴范围结束值
x_big_grid:x轴大格间距
x_small_grid:x轴小格间距
y_big_grid:y轴大格间距
y_small_grid:y轴小格间距
save_name:保存图片name
'''
def train(x, y,x_name,y_name,title,x_start,x_end,y_start,y_end,x_big_grid,x_small_grid,y_big_grid,y_small_grid,save_name):
    plt.rcParams['figure.figsize'] = (18.0, 15.0)  # 设置figure_size尺寸
    plt.rcParams['image.interpolation'] = 'nearest'  # 设置 interpolation style
    plt.rcParams['image.cmap'] = 'gray'  # 设置 颜色 style
    # 解决中文乱码问题
    plt.rcParams['font.sans-serif'] = ['Simhei']
    # 调用线性回归包
    model = LinearRegression()
    # train_test_split函数用于将矩阵随机划分为训练子集和测试子集，并返回划分好的训练集测试集样本和训练集测试集标签。
    # x和y均为数组源数据
    # train为训练数据,test为测试数据,train_size 和 test_size 规定了训练数据和测试数据的占比
    X_train, X_test, Y_train, Y_test = train_test_split(x, y, train_size=0.8, test_size=0.2)
    # 线性回归训练
    # 将一维数组X_train转化成二维数组
    # np.array(一维数组)[:, np.newaxis]
    model.fit(np.array(X_train)[:, np.newaxis], np.array(Y_train)[:, np.newaxis])  # 调用线性回归包

    a = model.intercept_  # 截距
    b = model.coef_  # 回归系数

    # 训练数据的预测值
    y_train_pred = model.predict(np.array(X_train)[:, np.newaxis])


    fig, ax = plt.subplots()
    # 绘制最佳拟合线：标签用的是训练数据的预测值y_train_pred
    ax.plot(X_train, y_train_pred, color='blue', linewidth=4, label="best line")
    # # 测试数据散点图
    ax.scatter(X_train, Y_train, color='darkgreen', label="train data",s=200)
    ax.scatter(X_test, Y_test, color='red', label="test data",s=200)
    ax.set_ylabel(y_name, fontsize=25)  # y轴标签
    ax.set_xlabel(x_name, fontsize=25)  # x轴标签
    ax.set_title(title, fontsize=30)  # title
    # 图标标签 为左上角
    plt.legend(loc=2, fontsize=26)
    fig.tight_layout()
    # 画网格
    ax = plt.gca()
    ax.xaxis.set_major_locator(plt.MultipleLocator(x_big_grid))
    ax.xaxis.set_minor_locator(plt.MultipleLocator(x_small_grid))  # 设置x从坐标间隔 0.1

    ax.yaxis.set_major_locator(plt.MultipleLocator(y_big_grid))
    ax.yaxis.set_minor_locator(plt.MultipleLocator(y_small_grid))  # 设置y从坐标间隔 0.1
    # 必须等比
    plt.xlim(x_start, x_end)
    plt.ylim(y_start, y_end)
    plt.xticks(fontsize=20, rotation=90)
    plt.yticks(fontsize=20)
    ax.grid(which='major', axis='x', linewidth=1, linestyle='-', color='0.75')  # 由每个x主坐标出发对x主坐标画垂直于x轴的线段
    ax.grid(which='minor', axis='x', linewidth=0.3, linestyle='-', color='0.75')  # 由每个x主坐标出发对x主坐标

    ax.grid(which='major', axis='y', linewidth=1, linestyle='-', color='0.75')
    ax.grid(which='minor', axis='y', linewidth=0.3, linestyle='-', color='0.75')
    # 保存图片到本地
    plt.savefig(u'C:/亿海蓝/img/' + save_name + '.png', bbox_inches='tight', pad_inches=0.0)
    # 展示img
    plt.show()

    # print(u"拟合参数:截距", a, u",回归系数：", b)
    print u'拟合参数:截距:',a
    print u'回归系数:',b
    print u"最佳拟合线: Y = ", round(a, 2), "+", round(b, 2), "* X"  # 显示线性方程，并限制参数的小数位为两位

5.读取，组装数据 调用求出最佳拟合线的方法：

# 船舶容积吨位（ship_GrossTonnage）和 船舶面积（长乘宽ship_LengthLOA* ship_MouldWidth） 线性回归图
def grossTonnage_area_linear_regression():
    # 调用读取postgre 数据源的方法（数据源如有缺失值 在sql中可剔除，如有异常值 可先进行处理 避免影响准确度）
    data = get_data.get_data()
    print data
    # 船舶容积吨位
    grossTonnage = []
    # 船舶面积
    area = []
    for i in range(len(data)):
        # 读取数据的第3列
        grossTonnage.append(data[i][3])
        # 读取数据的第4列
        area.append(data[i][4])
    print grossTonnage
    print area
    # 组装参数
    x_name = u'船舶面积'
    y_name = u'船舶容积吨位'
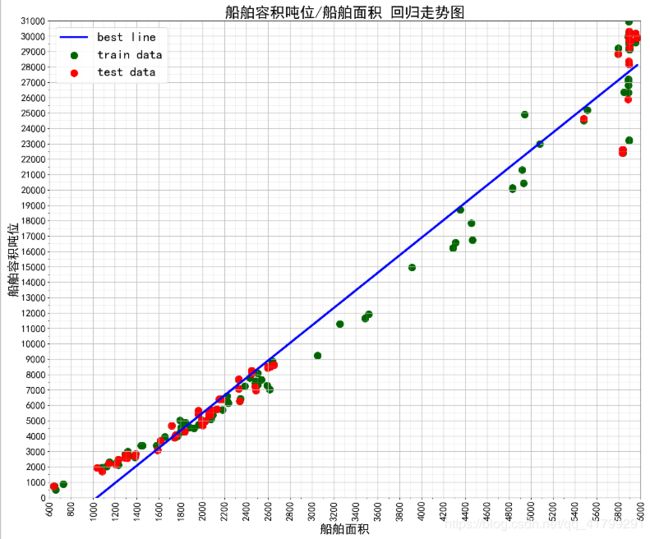
    title = u'船舶容积吨位/船舶面积 回归走势图'
    x_start = 600
    x_end = 6000
    y_start = 1
    y_end = 31000
    x_big_grid = 200
    x_small_grid = 100
    y_big_grid = 1000
    y_small_grid = 500
    save_name = u'船舶容积吨位和船舶面积回归走势图'
    # 调用回归模型训练 出图
    train(area, grossTonnage,x_name,y_name,title,x_start,x_end,y_start,y_end,x_big_grid,x_small_grid,y_big_grid,y_small_grid,save_name)

最终运行结果及回归走势图：

二：多元线性回归：（多变量）
其实实现多元回归和一元回归是差不多的 唯一的区别在于train_test_split()函数x的参数不止一个。
1.画出预测和测试走势图
2.求出最佳拟合方程

# -*- coding:utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import matplotlib.dates as mdate
import numpy as np
import pandas as pd
from pandas import DataFrame
import seaborn as sns
import get_data
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import sys
# reload(sys)
# sys.setdefaultencoding('utf8')



# 多元回归
def multiple_regression():
    # 调用线性回归包
    model = LinearRegression()
    adv_data = pd.read_csv(u"xx.csv")
    # 把读出来的数据转化成DataFrame格式的
    examDf = DataFrame(adv_data)
    # train_test_split() 里面的x，y通过examDf点列名点出来 x的话 就通过ix取指定的变量即可
    # 这里的examDf.ix[:,1:]就是需要的多变量
    X_train, X_test, Y_train, Y_test = train_test_split(examDf.ix[:,1:], examDf.ship_DeadWeight, train_size=0.8, test_size=0.2)
    # 线性回归训练
    model.fit(X_train, Y_train)  # 调用线性回归包

    a = model.intercept_  # 截距
    b = model.coef_  # 回归系数
    # print(u"拟合参数:截距", a, u",回归系数：", b)
    print u'拟合参数:截距:', a
    print u'回归系数:', b

    print "最佳拟合线: Y = ", round(a, 2), "+", round(b[0], 2), "* X1 + ", round(b[1], 2), "* X2"


    Y_pred = model.predict(X_test)  # 对测试集数据，用predict函数预测
    # 展示预测数据
    plt.plot(range(len(Y_pred)), Y_pred, 'red', linewidth=2.5, label="predict data")
    # 展示测试数据
    plt.plot(range(len(Y_test)), Y_test, 'green', label="test data")
    # 标签位置
    plt.legend(loc=2)
    plt.show()  # 显示预测值与测试值曲线

运行结果：