【比赛报告】Codeforces Round #506 (Div. 3) NOIP练习赛卷二

比赛链接
比赛日期：2018.9.24 用时：未计时 得分：未计分

A - Many Equal Substrings

Description

You are given a string $t$ consisting of $n$ lowercase Latin letters and an integer number $k$.

Let’s define a substring of some string $s$ with indices from $l$ to $r$ as $s[l\dots r]$.

Your task is to construct such string $s$ of minimum possible length that there are exactly $k$ positions $i$ such that $s[i\dots i+n-1]=t$. In other words, your task is to construct such string s of minimum possible length that there are exactly $k$ substrings of $s$ equal to $t$.

It is guaranteed that the answer is always unique.

Input

The first line of the input contains two integers $n$ and $k$ $(1\le n,k\le 50)$ — the length of the string $t$ and the number of substrings.

The second line of the input contains the string $t$ consisting of exactly $n$ lowercase Latin letters.

Output

Print such string $s$ of minimum possible length that there are exactly $k$ substrings of $s$ equal to $t$.

It is guaranteed that the answer is always unique.

Examples

Input

3 4
aba

Output

ababababa

Input

3 2
cat

Output

catcat

---

类似 $KMP$ 算法，我们求出一个最长的相同前缀后缀长度，即 $next$ 数组，然后输出 $k-1$ 个 $S[i],i\in [0,s.size()-next[n-1]]$，最后再输出 $S$。

#include
#include
using namespace std;
int nx[110];
int main()
{
	//freopen("in.txt","r",stdin);
	int n,k;
	string s;
	cin>>n>>k>>s;
	for(int i=1,j=0;i

总结

字符串算法没怎么写过题，很生疏。

---

B - Creating the Contest

题目链接

Description

You are given a problemset consisting of $n$ problems. The difficulty of the $i$-th problem is $a_i$. It is guaranteed that all difficulties are distinct and are given in the increasing order.

You have to assemble the contest which consists of some problems of the given problemset. In other words, the contest you have to assemble should be a subset of problems (not necessary consecutive) of the given problemset. There is only one condition that should be satisfied: for each problem but the hardest one (the problem with the maximum difficulty) there should be a problem with the difficulty greater than the difficulty of this problem but not greater than twice the difficulty of this problem. In other words, let $a_{i_1},a_{i_2},\cdots ,a_{i_p}$ be the difficulties of the selected problems in increasing order. Then for each $j$ from $1$ to $p-1,a_{i_j}+1\le a_{i_j}\times 2$ should hold. It means that the contest consisting of only one problem is always valid.

Among all contests satisfying the condition above you have to assemble one with the maximum number of problems. Your task is to find this number of problems.

Input

The first line of the input contains one integer $n$ $(1\le n\le 2\times 10^5)$ — the number of problems in the problemset.

The second line of the input contains n integers $a_1,a_2,\cdots ,a_n$ $(1\le a_i\le 10^9)$ — difficulties of the problems. It is guaranteed that difficulties of the problems are distinct and are given in the increasing order.

Output

Print a single integer — maximum number of problems in the contest satisfying the condition in the problem statement.

Examples

Input

10
1 2 5 6 7 10 21 23 24 49

Output

4

Input

5
2 10 50 110 250

Output

1

Input

6
4 7 12 100 150 199

Output

3

Note

Description of the first example: there are $10$ valid contests consisting of $1$ problem, $10$ valid contests consisting of $2$ problems $([1,2],[5,6],[5,7],[5,10],[6,7],[6,10],[7,10],[21,23],[21,24],[23,24])$, $5$ valid contests consisting of $3$ problems $([5,6,7],[5,6,10],[5,7,10],[6,7,10],[21,23,24])$ and a single valid contest consisting of $4$ problems $([5,6,7,10])$.

In the second example all the valid contests consist of $1$ problem.

In the third example are two contests consisting of $3$ problems: $[4,7,12]$ and $[100,150,199]$.

---

最初把题目看错了……交了两遍反应过来。就只需要贪心地把可加入的合并到一段里去，不能加入的开新的一段。

#include
#include
using namespace std;
const int N=2e5+10;
int a[N],ans,n;
int main()
{
	//freopen("in.txt","r",stdin);
	scanf("%d",&n);
	for(int i=0;i

总结

仔细审题很重要

---

C - Maximal Intersection

题目链接

Description

You are given $n$ segments on a number line; each endpoint of every segment has integer coordinates. Some segments can degenerate to points. Segments can intersect with each other, be nested in each other or even coincide.

The intersection of a sequence of segments is such a maximal set of points (not necesserily having integer coordinates) that each point lies within every segment from the sequence. If the resulting set isn’t empty, then it always forms some continuous segment. The length of the intersection is the length of the resulting segment or $0$ in case the intersection is an empty set.

For example, the intersection of segments $[1;5]$ and $[3;10]$ is $[3;5]$ (length $2$), the intersection of segments $[1;5]$ and $[5;7]$ is $[5;5]$ (length $0$) and the intersection of segments $[1;5]$ and $[6;6]$ is an empty set (length $0$).

Your task is to remove exactly one segment from the given sequence in such a way that the intersection of the remaining ($n-1$) segments has the maximal possible length.

Input

The first line contains a single integer $n$ $(2\le n\le 3\times 10^5)$ — the number of segments in the sequence.

Each of the next $n$ lines contains two integers $l_i$ and $r_i$ $(0\le l_i\le r_i\le 10^9)$ — the description of the $i$-th segment.

Output

Print a single integer — the maximal possible length of the intersection of ($n-1$) remaining segments after you remove exactly one segment from the sequence.

Examples

Input

4
1 3
2 6
0 4
3 3

Output

1

Input

5
2 6
1 3
0 4
1 20
0 4

Output

2

Input

3
4 5
1 2
9 20

Output

0

Input

2
3 10
1 5

Output

7

Note

In the first example you should remove the segment $[3;3]$, the intersection will become $[2;3]$ (length $1$). Removing any other segment will result in the intersection $[3;3]$ (length $0$).

In the second example you should remove the segment $[1;3]$ or segment $[2;6]$, the intersection will become $[2;4]$ (length 2) or $[1;3]$ (length $2$), respectively. Removing any other segment will result in the intersection $[2;3]$ (length $1$).

In the third example the intersection will become an empty set no matter the segment you remove.

In the fourth example you will get the intersection $[3;10]$ (length $7$) if you remove the segment $[1;5]$ or the intersection $[1;5]$ (length $4$) if you remove the segment $[3;10]$.

---

传说中的读懂题比写题耗时长。把每个区间左端点右端点分别扔进两个可重集里，每次去掉一对后用右端点最小减去左端点最大。

#include
#include
#include
using namespace std;
const int N=3e5+10;
multisetL,R;
int ans,n,l[N],r[N];
int main()
{
	//freopen("in.txt","r",stdin);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d%d",&l[i],&r[i]),L.insert(l[i]),R.insert(r[i]);
    for(int i=1;i<=n;i++)
    {
    	L.erase(L.find(l[i]));R.erase(R.find(r[i]));
    	ans=max(ans,*R.begin()-*L.rbegin());
    	L.insert(l[i]);R.insert(r[i]);
	}
	printf("%d\n",ans);
	return 0;
}

总结

STL大法好

---

D - Concatenated Multiples

Description

You are given an array $a$, consisting of $n$ positive integers.

Let’s call a concatenation of numbers $x$ and $y$ the number that is obtained by writing down numbers $x$ and $y$ one right after another without changing the order. For example, a concatenation of numbers $12$ and $3456$ is a number $123456$.

Count the number of ordered pairs of positions $(i,j)(i̸=j)$ in array a such that the concatenation of $a_i$ and $a_j$ is divisible by $k$.

Input

The first line contains two integers $n$ and $k$ $(1\le n\le 2\times 10^5,2\le k\le 10^9)$.

The second line contains $n$ integers $a_1,a_2,\cdots ,a_n$ $(1\le a_i\le 10^9)$.

Output

Print a single integer — the number of ordered pairs of positions $(i,j)(i̸=j)$ in array a such that the concatenation of $a_i$ and $a_j$ is divisible by $k$.

Examples

Input

6 11
45 1 10 12 11 7

Output

7

Input

4 2
2 78 4 10

Output

12

Input

5 2
3 7 19 3 3

Output

0

Note

In the first example pairs $(1,2),(1,3),(2,3),(3,1),(3,4),(4,2),(4,3)$ suffice. They produce numbers $451,4510,110,1045,1012,121,1210$, respectively, each of them is divisible by $11$.

In the second example all $n(n-1)$ pairs suffice.

In the third example no pair is sufficient.

---

记录每一个位数出现的模数，排序后统计每一个位数出现的需要的模数的个数，注意不要重复计算。

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=2e5+10;
int n,k,fac[11],len[N];
ll cnt,a[N];
vectorvx[11];
int main()
{
	//freopen("in.txt","r",stdin);
	scanf("%d%d",&n,&k);fac[0]=1;
	for(int i=1;i<=10;i++)fac[i]=fac[i-1]*10%k;
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&a[i]);
		len[i]=log10(a[i])+1;
		vx[len[i]].push_back(a[i]%k);
	}
	for(int i=0;i<=10;i++)sort(vx[i].begin(),vx[i].end());
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=10;j++)
		{
			int mod=(a[i]*fac[j])%k;
			int key=(k-mod)%k;
			int l=lower_bound(vx[j].begin(),vx[j].end(),key)-vx[j].begin();
			int r=upper_bound(vx[j].begin(),vx[j].end(),key)-vx[j].begin();
			cnt+=r-l;
			if(len[i]==j&&(mod+a[i]%k)%k==0)cnt--;//去掉多算的 
		}
	}
	printf("%lld\n",cnt);
	return 0;
}

总结

这题看数据范围发现暴力不可解，可以在每一个位数下记录出现的 $k$ 模数，再进行计算。可以通过位数和模数来判断是否把自己给算进去了。

---

E - Tree with Small Distances

题目链接

Description

You are given an undirected tree consisting of $n$ vertices. An undirected tree is a connected undirected graph with $n-1$ edges.

Your task is to add the minimum number of edges in such a way that the length of the shortest path from the vertex $1$ to any other vertex is at most $2$. Note that you are not allowed to add loops and multiple edges.

Input

The first line contains one integer $n$ $(2\le n\le 2\times 10^5)$ — the number of vertices in the tree.

The following $n-1$ lines contain edges: edge $i$ is given as a pair of vertices $u_i,v_i$ $(1\le ui,vi\le n)$. It is guaranteed that the given edges form a tree. It is guaranteed that there are no loops and multiple edges in the given edges.

Output

Print a single integer — the minimum number of edges you have to add in order to make the shortest distance from the vertex $1$ to any other vertex at most $2$. Note that you are not allowed to add loops and multiple edges.

Examples

Input

7
1 2
2 3
2 4
4 5
4 6
5 7

Output

2

Input

7
1 2
1 3
2 4
2 5
3 6
1 7

Output

0

Input

7
1 2
2 3
3 4
3 5
3 6
3 7

Output

1

Note

The tree corresponding to the first example:

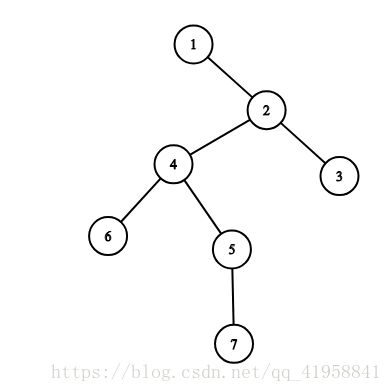
The answer is $2$, some of the possible answers are the following: $[(1,5),(1,6)],[(1,4),(1,7)],[(1,6),(1,7)]$.

The tree corresponding to the second example:

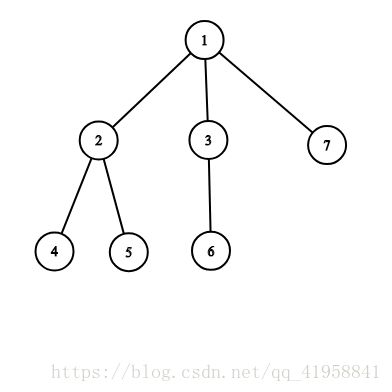
The answer is $0$.

The tree corresponding to the third example:

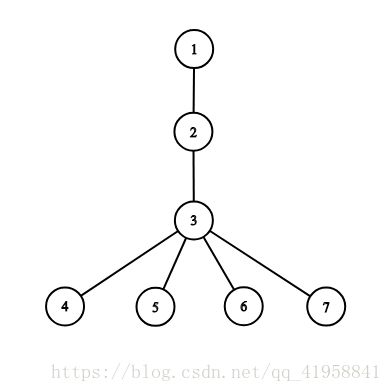
The answer is $1$, only one possible way to reach it is to add the edge $(1,3)$.

---

要求连最少的边使以 $1$ 为根的树上所有子节点深度不超过 $2$ 。$dfs$ 一遍求出每个点的深度，把每个深度超过 $2$ 的点加入堆中。每次取出堆顶节点，如果没有被更新，就向他的父节点连一条返祖边，然后遍历与父节点直接相连的节点标记。

#include
#include
#include
using namespace std;
const int N=2e5+10;
int dep[N],fa[N],n,hd[N],tot,vis[N];
struct Edge{
	int v,nx;
}e[N<<1];
void add(int u,int v)
{
	e[tot].v=v;
	e[tot].nx=hd[u];
	hd[u]=tot++;
}
void dfs(int u,int f)
{
	for(int i=hd[u];~i;i=e[i].nx)
	{
		int v=e[i].v;
		if(v==f)continue;
		fa[v]=u;dep[v]=dep[u]+1;
		dfs(v,u);
	}
}
int main()
{
	//freopen("in.txt","r",stdin);
	memset(hd,-1,sizeof(hd));
	scanf("%d",&n);
	int u,v,ans=0;
	for(int i=1;i >q;
	for(int i=1;i<=n;i++)if(dep[i]>2)q.push(make_pair(dep[i],i));
	while(q.size())
	{
		u=q.top().second;q.pop();
		if(vis[u])continue;
		ans++;vis[fa[u]]=1;
		for(int i=hd[fa[u]];~i;i=e[i].nx)vis[e[i].v]=1;
	}
	printf("%d\n",ans);
	return 0;
}

总结

可能可以证明每次去最深的节点是最优的，反例是容易举出的。

---

F - Multicolored Markers

题目链接

Description

There is an infinite board of square tiles. Initially all tiles are white.

Vova has a red marker and a blue marker. Red marker can color $a$ tiles. Blue marker can color $b$ tiles. If some tile isn’t white then you can’t use marker of any color on it. Each marker must be drained completely, so at the end there should be exactly $a$ red tiles and exactly $b$ blue tiles across the board.

Vova wants to color such a set of tiles that:

they would form a rectangle, consisting of exactly $a+b$ colored tiles;
all tiles of at least one color would also form a rectangle.
Here are some examples of correct colorings:

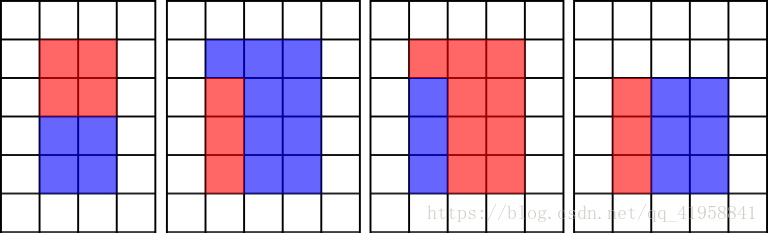
Here are some examples of incorrect colorings:

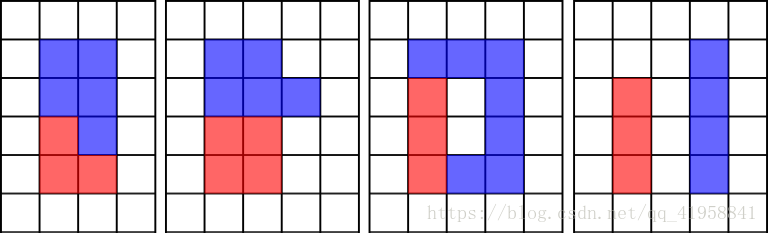
Among all correct colorings Vova wants to choose the one with the minimal perimeter. What is the minimal perimeter Vova can obtain?

It is guaranteed that there exists at least one correct coloring.

Input

A single line contains two integers $a$ and $b$ $(1\le a,b\le 10^{14})$ — the number of tiles red marker should color and the number of tiles blue marker should color, respectively.

Output

Print a single integer — the minimal perimeter of a colored rectangle Vova can obtain by coloring exactly $a$ tiles red and exactly $b$ tiles blue.

It is guaranteed that there exists at least one correct coloring.

Examples

Input

4 4

Output

12

Input

3 9

Output

14

Input

9 3

Output

14

Input

3 6

Output

12

Input

506 2708

Output

3218

Note

The first four examples correspond to the first picture of the statement.

Note that for there exist multiple correct colorings for all of the examples.

In the first example you can also make a rectangle with sides $1$ and $8$, though its perimeter will be $18$ which is greater than $8$.

In the second example you can make the same resulting rectangle with sides $3$ and 44$, but red tiles will form the rectangle with sides $1$ and $3$ and blue tiles will form the rectangle with sides $3$ and $3$.

---

参考了大佬题解
显然边长必须得整除面积（废话），能够想到把能整除 $a$ 或 $b$ 的边长都存上，然后碰到能整除 $a+b$ 的边长就查找是否存在。但是这样错了，参考了大佬的题解后想明白了，不一定要刚好存在，长度可以包含最小的能整除 $a$ 或 $b$ 的边长就可以了。

#include
#include
using namespace std;
typedef long long ll;
ll a,b,ans=1e18;
sets;
int main()
{
    scanf("%lld%lld",&a,&b);
    for(ll len=1;len*len<=a+b;len++)
    {
    	if(a%len==0)s.insert(a/len);
    	if(b%len==0)s.insert(b/len);
		if((a+b)%len==0&&*s.begin()<=(a+b)/len)ans=min(ans,len+(a+b)/len);
	}
	printf("%lld\n",ans*2);
	return 0;
}

总结

审题不仔细，写的时候没有想到可以不是刚好整除 $a$ 或 $b$ 而是包含能整除 $a$ 或 $b$ 的最小边长。

---

赛后总结

老早就听说了codeforces但是一直没时间去打，今天在vjudge上clone了一个比赛自己试了试，结果第一个难关就是读懂题，然后T1就炸，然后各种事就没有再打了。
虽然只是div3，但还是把我骚到了。没有出现什么算法，就是一些很基本的东西，只是有些操作有些麻人。
codeforces的题挺好的，以后还是开div2。
联赛将至，自己还是这么弱。但是做出了承诺就不能食言。前方无路是高墙，就打破它得到路。