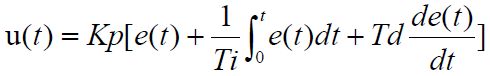一文读懂pid控制器
文章目录
- PID控制器
- 1. 控制器
- 1.1 电机速度控制系统
- 1.2 温度或水位控制系统
- 1.3 小小总结
- 2. PID
- 3. 模拟式PID
- 4. 数字式PID
- 4.1 位置式PID算法
- 4.1.2 位置式pid算法的缺点
- 4.2 增量式PID算法
- 4.2.2 增量式pid的优点
- 4.3 位置式pid和增量式pid的抉择
- 4.4 位置式pid和增量式pid仿真
PID控制器
1. 控制器
在研究PID控制器前,必须先想一个问题,控制器的作用到底是什么?相信不少同学在学习自动控制原理的时候,接触最多的是:直接对传递函数进行分析,比如研究某个传函的阶跃响应?幅频特性?稳态误差?根据劳斯判据,根轨迹研究根的分布以判断系统的稳定型?
那么控制器又是哪里冒出来的?自控中的开环系统或者闭环系统不能解决问题么?其实这是我们认识狭隘了,这句话本身就是不对的,往下看。
举两个实例:
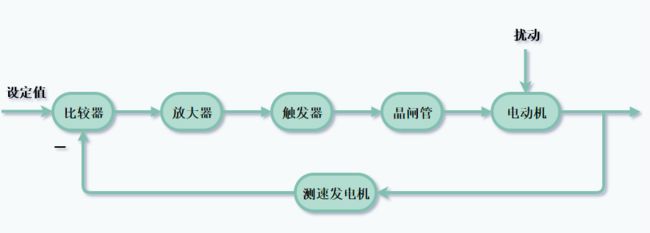
1.1 电机速度控制系统
- 当出现扰动而使得电机的转速偏离设定值时,测速电动机充当检测变送环节的角色,而它的输出和设定值之间就会出现一个偏差信号(电压信号)
- 这个偏差信号通常是比较小的,所以需要放大器对其进行放大
- 而这个放大后的电压信号则是触发器的控制电压,控制晶闸管的关断时间,进而调节电动机的电枢电压,从而调节转速直到等于设定值
在这个控制系统中,电动机显然是被控对象,而它的转速变化规律是可以抽象为一个数学模型的,也就是传递函数;而其他的环节,则是为了共同产生一个控制信号来作为电动机的输入。
我们可以把比较器称为本文中的调节器,或者将比较器+放大器称为调节器,这不是重点,无伤大雅。
值得注意的是:这个系统中的所有环节,其控制规律都可以抽象为若干个传递函数
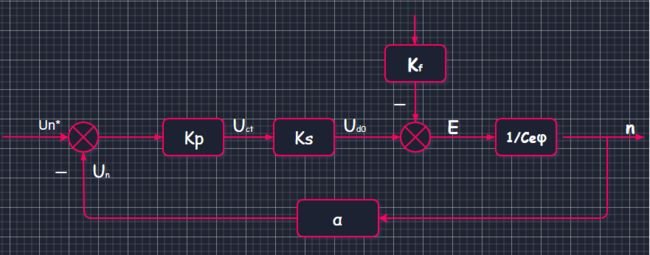
- Un*为设定值,Un为测量变送的反馈值
- 两者偏差去调节触发器控制电压Uct,控制规律为
Kp - 通过晶闸管控制电动机回路总电压Ud0,控制规律为
Ks - Ud0 - 电枢总电阻电压即为电动机电动势E
- E = Ceφn,得到输出转速;测速发电机根据转速反馈电压信号,控制规律
α
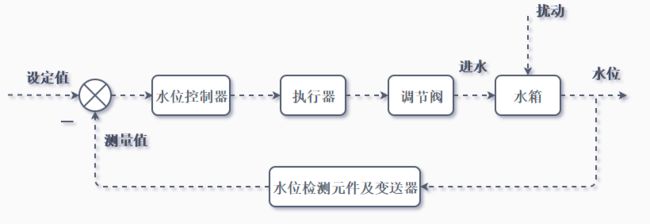
1.2 温度或水位控制系统
这个应该是比较简单的过程控制,实际水位低于设定水位时,控制器则作用于执行机构去增大调节阀开度,增加进水流量。
1.3 小小总结
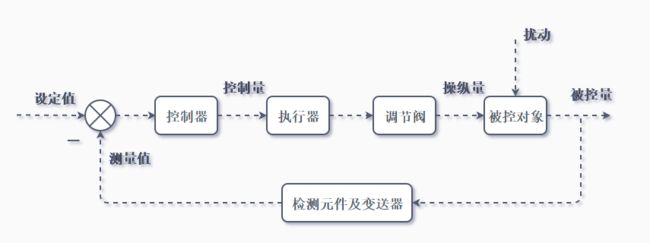
不要总是孤立控制器,它们是控制被控对象的必要环节。
这里给出一般的闭环控制系统框图
不要单纯的认为只有被控对象才有传递函数,每一个环节都有其相应的控制规律,都可以抽象为一个数学模型,用对应的传递函数来表达。就像最小拍控制器设计中,我们根据输入信号选择整个系统的闭环传函,进而确定控制器的脉冲传递函数。
总结:对于闭环系统来说,控制器的输入是偏差信号,输出则是控制信号,去控制执行机构,进而调节被控对象。
而闭环控制系统,设计目的就是系统输出对输入的跟随能力。
2. PID
- P:比例控制器,对系统产生的偏差能够迅速做出反应;但是比例控制器不能消除余差,不过随着比例系数的增大,余差会减小,同时系统输出振荡次数增加,稳定性也会下降,调节时间加长
关于不能消除余差这一点,从数学角度是可以解释的,求一下余差即可。当然直想也是可以理解的:对于一个速度控制系统,某时刻负载减小,导致转速上升,比例控制器作用于执行机构使得转速下降,假如转速可以下降到设定转速,那么此时负载依然是小于额定负载的,转速依然会上升;所以反证得,最后余差是肯定会存在的。
-
I:积分控制器,积分控制是可以消除余差的,体现于偏差消失后,积分控制器的输出是可以保持前时刻的输出;但是积分控制器的控制动作比较缓慢,一般不单独使用;随着积分系数的增大(时间常数的减小),系统的稳定性下降。
-
D:微分控制器,够体现出当前误差的变化趋势,在偏差出现或变化的瞬间,立即产生强烈的调节作用,从而加快系统的动作速度,减少调节时间;但是由于微分对静态偏差毫无控制能力(偏差存在,但是不变化,控制器输出为0),所以一般不单独使用。并且在纯比例作用的基础上增加微分作用可以提高系统稳定性。
总结:讲比例,积分,微分三种控制规律结合在一起,只要三项控制作用的强度配合得当,就既能快速调节,又能消除余差,从而得到满意的控制效果。
3. 模拟式PID
模拟pid控制器的算法:
- u(t) 为控制器输出,e(t) 为控制器输入,即偏差信号:
e(t) = r(t) - y(t) - Kp 为比例系数,Ti 为积分时间常数,Td 为微分时间常数
参数设置:Kp = 0.5, Ki = 0.2, Kd = 1;输出结果:
模拟pid局限性
- 功能单一,灵活性差
- 信息分散,所用仪表多,且监视不方便
- 接线过多,系统维护难度大
随着计算机等技术的发展,数字控制器日益成为工业生产中占据主导地位的控制器。
4. 数字式PID
对模拟pid控制器进行离散化处理,用后向差分代替微分得:(具体细节不细说)
4.1 位置式PID算法
- Kp,Ki,Kd为比例,积分,微分的三个重要参数
- k是采样序列号,k=0,1,2,3…
- Uk第k次采样时刻控制器输出值
- ek第k次采样时刻偏差,e(k-1)第k-1次采样偏差值,e(k-2)第k-2次采样偏差值
- 位置式pid控制器的输入为系统的偏差值,输出为uk,即偏差的组合
4.1.2 位置式pid算法的缺点
- 控制器输出与过去的各个状态有关,运算量大
- 计算机出现故障,u(k)的大幅度变化会引起执行机构位置的大幅度变化
4.2 增量式PID算法
由位置式pid第k次输出 - 第k-1次输出 得到增量式pid算法:
![]()
增量式pid算法表示的是控制机构(阀门,步进电机等)的调节增量,即k时刻相对于k-1时刻的调节增量。
值得注意的是:采用增量式pid算法的控制器输出值为调节增量。
从这里也可以得出位置式pid算法的另一种表示形式:
u(k) = u(k - 1) + Δu
可以说,位置式pid算法和增量式pid算法是pid算法的两种表现形式,从本质上讲二者是一致的。
4.2.2 增量式pid的优点
- 算式中不需要累加;控制增量Δu(k)的确定仅与最近3次的采样值有关
- 计算机每次只输出控制增量,对应执行机构位置的变化量,不易引起过程的异常操作
- 手动—自动切换时冲击小。当控制从手动向自动切换时,
可以作到无扰动切换
4.3 位置式pid和增量式pid的抉择
在实际使用中应该使用位置式还是增量式,关键看执行机构的特性:
- 如果执行机构具有积分特性(如步进电机,具有齿轮传递特性的位置执行机构等),应该使用增量式pid算法
- 如果执行机构没有积分特性,则应该使用位置式pid算法
4.4 位置式pid和增量式pid仿真
function [] = my_simulink_pid()
% 离散模型
ts = 0.001; % 采样时间
sys = tf(400, [1, 50, 0]); % 传递函数
d_sys = c2d(sys, ts, 'z'); % 传递函数离散化
[num, den] = tfdata(d_sys, 'v'); % 提取分子分母
% pid参数
kp = 10; ki = 2; kd = 15;
% 初始化信号值
y_feed = 0; % 当前反馈值
y_prev1 = 0; % 前一次输出值
y_prev2 = 0; % 前前一次输出值
u_prev1 = 0; % 前一次控制器输出值
u_prev2 = 0; % 前前一次控制器输出值
e_prev1 = 0; % 前一次偏差
e_prev2 = 0; % 前前一次偏差
x = [0, 0, 0]; % p i d 分别的输出
for k = 1:1:3000
time(k) = k*ts; % 时间序列,用于画图
r_in(k) = 1; % 输入序列,单位阶跃
e(k) = r_in(k) - y_feed; % 当前时刻偏差
delta_u = kp*x(1) + ki*x(2) + kd*x(3);
% 位置式 PID算法
% u(k) = u_prev1 + delta_u;
% 增量式 PID算法
u(k) = delta_u;
% 对输出限幅
if u(k) >= 10
u(k) = 10
end
if u(k) <= -10
u(k) = -10
end
% 值得注意得是,这是输出序列的差分方程;得到他的步骤:
% 1. z变换得到脉冲传递函数
% 2. 分子分母乘上z的最高次幂的导数,本例中就是z^-2
% 3. 交叉相乘,整理
% 4. z反变换
y_out(k) = -den(2)*y_prev1- den(3)*y_prev2 + num(2)*u_prev1 + num(3)*u_prev2; % 系统输出序列
y_feed = y_out(k); % 反馈值
u_prev2 = u_prev1; % 更新控制器输出
u_prev1 = u(k);
y_prev2 = y_prev1; % 更新系统输出
y_prev1 = y_out(k);
x(1) = e(k) - e_prev1;
x(2) = e(k);
x(3) = e(k) - 2*e_prev1 + e_prev2;
e_prev2 = e_prev1; % 更新偏差
e_prev1 = e(k);
end
% 画图
figure(1);
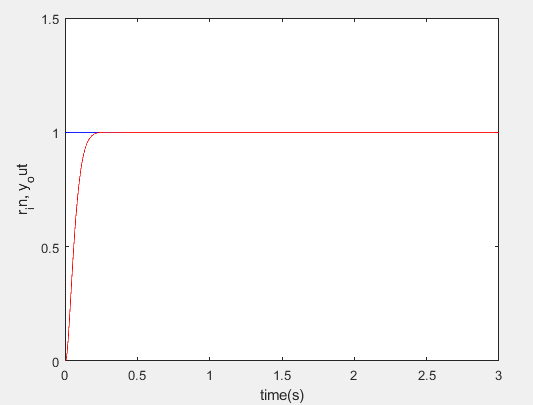
plot(time, r_in, 'b', time, y_out, 'r');
axis([0, 3, 0, 1.5]); % 确定坐标轴范围
xlabel('time(s)'),ylabel('r_in, y_out'); % 系统输出和系统输入的曲线
figure(2);
plot(time, r_in, 'b', time, u, '--k');
axis([0, 3, -0.2, 2.5]); % 确定坐标轴范围
xlabel('time(s)'),ylabel('r_in, u_out'); % 控制器输出和系统输入的曲线
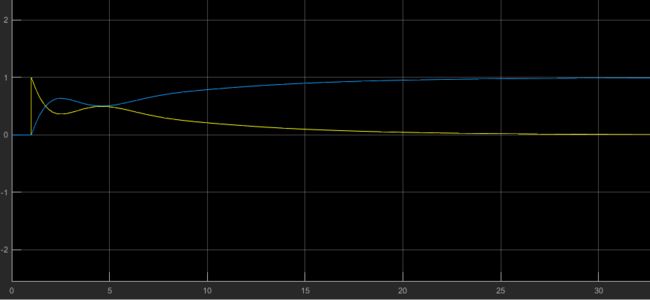
仿真结果:
增量式pid——系统食输出和系统输入曲线图
增量式pid——控制器输出和系统输入曲线图
关于位置式pid算法,在代码中也有标注,只需要加前一时刻控制器输出即可,至于参数的整定,在这里不详细说明。
欢迎指出不足,共同进步,谢谢~