机器学习知识点笔记(一)
目录
什么是机器学习?
如何寻找这个函数?
机器学习三板斧
学习路线
奥卡姆剃刀(Occam's razor)原理
bias偏差、variance方差
监督学习
L1范数和L2范数的区别和作用?
为什么L1范数会使权值稀疏?
为什么要稀疏?参数稀疏有什么好处呢?
为什么L2范数可以防止过拟合?
什么是模型过拟合,列举模型过拟合的原因及解决办法?
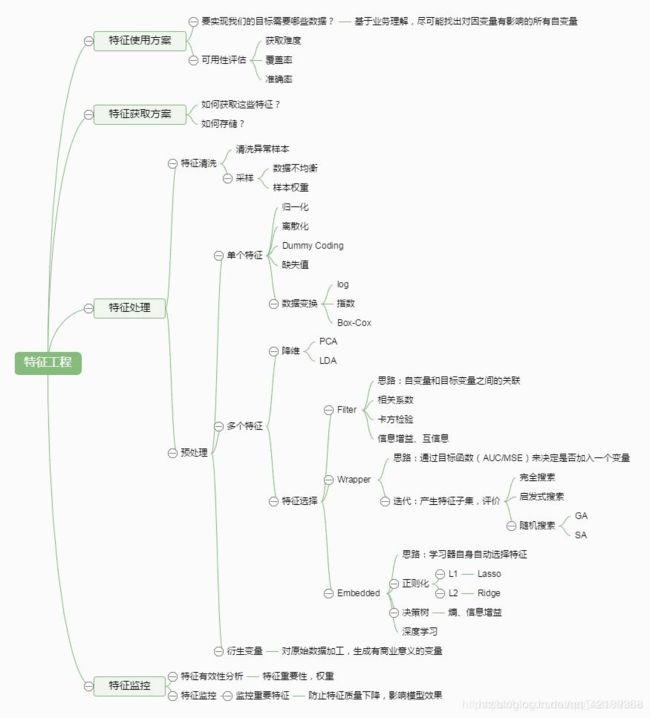
对特征进行挑选的方法有哪些?
机器学习中为什么要经常对数据做归一化处理?
什么是机器学习?
机器学习=寻找一种函数
如何寻找这个函数?
①定一个函数集合
②判断函数的好坏
③选择最好的函数
机器学习三板斧
①设计模型model
②判断模型的好坏
③选择最好的函数,优化模型
3.1修改模型,增加数据维度
3.2增加正则因子,使函数更加平滑,让参数w取值更小。(x变化较小时,整个函数结果不会变化太大,结果更准)
学习路线
监督学习:有数据标注情况下学习(回归、分类)
半监督学习:训练数据中带标记的数据不够多
迁移学习:在已学习基础上,做看似和以前学习不相关的事情,但实际效果很好(在猫狗识别基础识别大象老虎等)
非监督学习:没有具体标注数据的情况下学习(机器阅读、机器绘画)
结构化学习:超越简单的回归和分类,产生结构化的结果(如图片、语言、声音)
奥卡姆剃刀(Occam's razor)原理
在所有可能选择的模型中,我们应该选择能够很好地解释已知数据并且十分简单的模型。
bias偏差、variance方差
偏差:指与目标结果的偏移量,与目标距离远的是大偏差,与目标距离近的偏差小。
方差:描述的是稳定性,是否集中在目标区域,相对分散的是高方差,相对集中的是低方差。
监督学习
监督机器学习问题无非就是“minimizeyour error while regularizing your parameters”,也就是在规则化参数的同时最小化误差。最小化误差是为了让我们的模型拟合我们的训练数据,而规则化参数是防止我们的模型过分拟合我们的训练数据。
训练误差小并不是我们的最终目标,我们的目标是希望模型的测试误差小,也就是能准确的预测新的样本。
一般来说,监督学习可以看做最小化下面的目标函数:
![]()
第一项L(yi,f(xi;w)) 衡量模型(分类或回归)对第i个样本的预测值f(xi;w)和真实标签yi之间的误差,要求这一项最小,模型尽量拟合训练数据。不仅要保证训练误差最小,更希望模型测试误差小,所以需加上对参数w的规则化函数Ω(w)去约束模型尽量简单。
对于第一项Loss函数,如果是Square loss,就是最小二乘;如果是Hinge Loss,那就是著名的SVM了;如果是exp-Loss,那就是Boosting了;如果是log-Loss,那就是Logistic Regression了;还有等等。不同的loss函数,具有不同的拟合特性,这个也得就具体问题具体分析的。
规则化函数Ω(w)也有很多种选择,一般是模型复杂度的单调递增函数,模型越复杂,规则化值就越大。比如,规则化项可以是模型参数向量的范数。然而,不同的选择对参数w的约束不同,取得的效果也不同,但在论文中常见的都聚集在:零范数、一范数、二范数、迹范数、Frobenius范数和核范数等等。这么多范数,到底它们表达啥意思?具有啥能力?什么时候才能用?什么时候需要用呢?
L1范数和L2范数的区别和作用?
范数:指的是向量的长度
L1范数是指向量中各个向量元素的绝对值之和。
L2范数(岭回归ridge regression或权值衰减weight decay)是指各个各个向量元素的平方和再开方。
L1范式相当于L0范式,使特征更多成为0,即特征稀疏化(L0范数很难优化求解,所以用的L1范式),方便特征提取。
L2范数可以防止过拟合,提升模型的泛化能力。
为什么L1范数会使权值稀疏?
任何的规则化算子,如果他在Wi=0的地方不可微,并且可以分解为一个“求和”的形式,那么这个规则化算子就可以实现稀疏。
为什么要稀疏?参数稀疏有什么好处呢?
特征选择(Feature Selection)
稀疏规则化算子的引入是为了完成特征自动选择的光荣使命,它会学习地去掉这些没有信息的特征,也就是把这些特征对应的权重置为0。
可解释性(Interpretability)
模型更容易解释。例如患某种病的概率是y,然后收集到的数据x是1000维的,也就是需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设这是个回归模型:y=w1*x1+w2*x2+…+w1000*x1000+b(当然了,为了让y限定在[0,1]的范围,一般还得加个Logistic函数)。通过学习,如果最后学习到的w*就只有很少的非零元素,例如只有5个非零的wi,那么我们就有理由相信,这些对应的特征在患病分析上面提供的信息是巨大的,决策性的。也就是说,患不患这种病只和这5个因素有关,那医生就好分析多了。
为什么L2范数可以防止过拟合?
让L2范数的规则项||W||2最小,可以使得W的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0。而越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。
什么是模型过拟合,列举模型过拟合的原因及解决办法?
据噪声导致的过拟合:噪声具有一定的随机性与欺骗性,如果把噪声作为有效信息的话,将会导致过拟合。
缺乏代表性样本导致的过拟合:训练数据集不能很好的反应整体分布可能会导致过拟合;训练数据集较小,但模型过度细化会导致过拟合。
从定量角度来讲,过拟合常常表现为模型的方差过大,而欠拟合则表现为模型的偏差过大
对特征进行挑选的方法有哪些?
通常来说,从两个方面考虑来选择特征:
特征是否发散:如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用。
特征与目标的相关性:这点比较显见,与目标相关性高的特征,应当优选选择。除方差法外,本文介绍的其他方法均从相关性考虑。
根据特征选择的形式:
Filter:过滤法,按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。通过该方法选出来的特征与具体的预测模型没有关系,因此具有更好的泛化能力。
Wrapper:包装法,根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征。围绕一定的预测模型,预测模型的估计误差一定程度上反映了特征的有用性。
Embedded:集成法,先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。
机器学习中为什么要经常对数据做归一化处理?
- 归一化后加快了梯度下降求最优解的速度;
- 归一化有可能提高精度
常见的有这两种:
最值归一化。比如把最大值归一化成1,最小值归一化成-1;或把最大值归一化成1,最小值归一化成0。适用于本来就分布在有限范围内的数据。
均值方差归一化,一般是把均值归一化成0,方差归一化成1。适用于分布没有明显边界的情况,受outlier影响也较小。
参考:
https://mp.weixin.qq.com/s/Do2LCjo0bSBudp-Syj634Q
https://www.cnblogs.com/weizc/p/5778678.html
https://www.zhihu.com/question/20455227/answer/370658612