回溯法、分支限界法解决旅行商TSP问题
文章目录
- TSP问题描述
- 回溯法解tsp问题(深度优先)
- 代码
- 基站数据
- 运行结果
- 分支限界法解tsp问题(广度优先)
- 代码
- 运行结果
- 结果分析
TSP问题描述
旅行商从驻地出发,经过每个需要访问的城市一次且只有一次,并最终返回出发点。如何安排路线,使旅行总路程最短?即求解最短哈密顿回路。
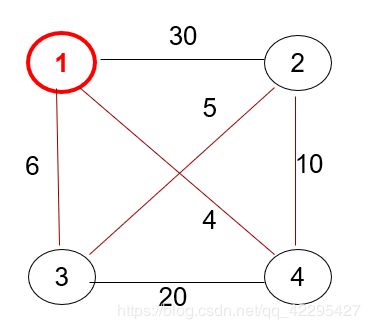
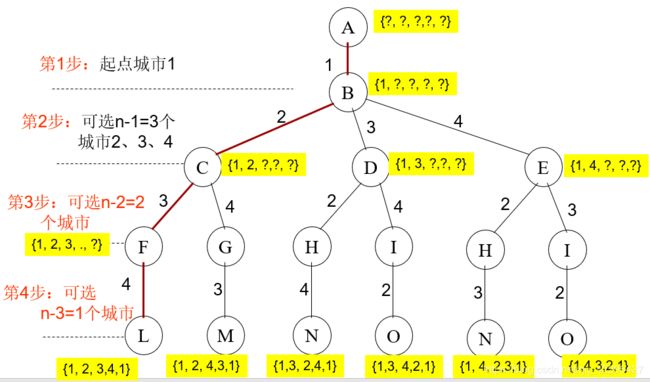
回溯法解tsp问题(深度优先)
以深度优先的方式,从根节点开始,依次扩展树节点,直到达到叶节点——搜索过程中动态产生解空间
代码
#include基站数据
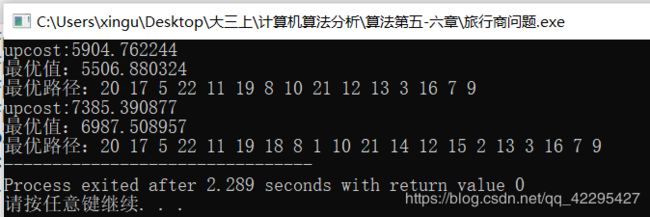
运行结果
分支限界法解tsp问题(广度优先)
代码
#includex[0]][p->x[j]]x[0]][p->x[j]];
}
p->lb+=min;
min=NoEdge;*/
for(int i=p->s+1;i<n;i++){//进入/离开未遍历城市时,各未遍历城市带来的最小路径成本
for(int j=0;j<n;j++){
if(w[p->x[i]][p->x[j]]<min){
min=w[p->x[i]][p->x[j]];
min1=j;
}
}
p->lb+=min;
min=NoEdge;
for(int j=0;j<n;j++){
if(w[p->x[i]][p->x[j]]<min&&j!=min1)
min=w[p->x[i]][p->x[j]];
}
p->lb+=min;
min=NoEdge;
}
p->lb/=2;
if(p->s==n-1)
p->lb+=w[p->x[n-1]][p->x[0]];
else{
//从当前已经走过的第一个城市出发,走向最近的1个未遍历城市的距离和
for(int j=p->s+1;j<n;j++){
if(w[p->x[0]][p->x[j]]<min)
min=w[p->x[0]][p->x[j]];
}
p->lb+=min;
min=NoEdge;
}
/*for(int i=0;ix[i]);
printf("\n%lf\n",p->lb);*/
}
void BBTSP(int v[],int n)//回溯法求解
{//解旅行售货员问题的优先队列式分支限界法
/*初始化最优队列的头结点*/
head = (MinHeapNode*)malloc(sizeof(MinHeapNode));
head->cc = 0;
head->x = 0;
head->lb = 0;
head->next = NULL;
head->s = 0;
MinHeapNode *E ;
E = (MinHeapNode*)malloc(sizeof(MinHeapNode));
E->x = new int[n];
for(int i = 0; i <n; i++)
E->x[i] = x[i+1];
E->s = 0;
low_cost(E,n);
E->cc = 0;
E->next = NULL; //初始化当前扩展节点
//搜索排列空间树
while(E->s >=0)
{//非叶结点
//printf("s:%d\n",E->s);
//printf("chuli:%d\n",E->x[E->s]);
//printlen();
//printf("-------s:%d---------\n",E->s);
if(E->s == n - 1)//到达叶节点
{
/*
如果该叶结点的路径值和所有节点的lb相比是最小的,输入最优解算法结束
否则更新上界
*/
/*printf("!!!!!!\n");
for(int k=0;kx[k]);
printf("\n");*/
if(w[E->x[E->s]][E->x[0]]==NoEdge){//无法形成回路
//printf("11111\n");
DeleteMin(E);
continue;
}
else{
E->cc+=w[E->x[E->s]][E->x[0]];
bestw=E->cc;
for(int i=0;i<n;i++)
bestx[i+1]=E->x[i];
break;
}
}else
{/*扩展子节点,将可行子节点加入优先队列中*/
//printf("2,upcost:%lf\n",upcost);
for(int i = E->s + 1; i < n; i++)
if(w[E->x[E->s]][E->x[i]] != NoEdge)
{ /*当前扩展节点到其他节点有边存在*/
//可行儿子结点
//printf("3\n");
double cc = E->cc + w[E->x[E->s]][E->x[i]]; /*加上节点i后当前节点路径*/
MinHeapNode* N;
N = (MinHeapNode*)malloc(sizeof(MinHeapNode));
N->x = new int[n];
for(int j = 0; j < n; j++)
N->x[j] = E->x[j];
N->x[E->s + 1] = E->x[i];
N->x[i] = E->x[E->s + 1];
N->cc = cc; /*更新当前路径距离*/
N->s = E->s + 1; /*更新当前节点*/
low_cost(N,n);
//printf("cc:%lf\n",N->cc);
//printf("lb:%lf\n",N->lb);
if(N->lb<=upcost)
{//子树可能含最优解,结点插入最小堆
/*添加当前路径*/
//printf("add:%d\n",N->x[E->s+1]);
//printf("4\n");
N->next = NULL;
Insert(N); /*将这个可行儿子结点插入到活结点优先队列中*/
}
}
free(E);
}//完成结点扩展
DeleteMin(E);//取下一扩展结点
if(E == NULL)
break; //堆已空
}
if(bestw == NoEdge)
return ;//无回路
while(true)
{//释放最小堆中所有结点
free(E->x);
DeleteMin(E);
if(E == NULL)
break;
}
}
int main(){
FILE* fp1=fopen("22基站.txt","r");
FILE* fp2=fopen("15基站.txt","r");
FILE* fp3=fopen("20基站.txt","r");
FILE* fp4=fopen("30基站.txt","r");
w=(double**)malloc(sizeof(double*)*(NUM+1));
for(int i=0;i<=NUM;i++)
w[i]=(double*)malloc(sizeof(double)*(NUM+1));
for(int i=1;i<=22;i++)//读入22基站的连接矩阵
for(int j=1;j<=22;j++)
fscanf(fp1,"%lf",&w[i][j]);
for(int i=1;i<=15;i++)//读入15个基站的初始顺序
fscanf(fp2,"%d",&x[i]);
up_cost(1,15);//求问题上界
cw=0.0;
printf("upcost:%lf\n",upcost);
BBTSP(bestx,15);
//backtrackTSP(2,15);
printf("最优值:%lf\n",bestw);
printf("最优路径:");
for(int i=1;i<=15;i++)
printf("%d ",bestx[i]);
cw=0.0;
bestw=99999.0;
for(int i=1;i<=20;i++)//读入20个基站的初始顺序
fscanf(fp3,"%d",&x[i]);
up_cost(1,20);//求问题上界
cw=0.0;
printf("\nupcost:%lf\n",upcost);
BBTSP(bestx,20);
printf("最优值:%lf\n",bestw);
printf("最优路径:");
for(int i=1;i<=20;i++)
printf("%d ",bestx[i]);
}
运行结果
结果分析
明显可以看出分支限界法求解所用的时间是少于回溯法的,毕竟前者设计上便是以空间换时间。回溯法的时间复杂度是 O ( n ! ) O(n!) O(n!),而分支限界法的时间复杂度是 O ( n 2 × 2 n ) \mathrm{O}\left(n^{2} \times 2^{n}\right) O(n2×2n)