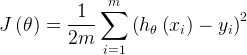经典算法（一）：线性回归

 前言

 1. 基本形式

 2. 损失函数

     2.1 损失函数

           2.1.1 最小二乘法

           2.1.2 极大似然估计

     2.2 正规方程法

           2.2.1 一般形式

           2.2.2 矩阵形式

     2.3 梯度下降法

           2.3.1 梯度下降法的代数方式描述

           2.3.2 梯度下降法的矩阵方式描述

           2.3.3  梯度下降的算法调优

           2.3.4  梯度下降法的类型

 3. 欠/过拟合

    3.1 欠拟合

           3.1.1  何为欠拟合？

           3.1.2  解决方法

    3.2 过拟合   

           3.2.1  何为过拟合？

           3.2.2  解决方法

 4. 正则化

    4.1 L0范数

    4.2 L1范数与Lasso

    4.3 L2范数与Ridge

    4.4 Elastic Net

    4.5  L1为稀疏约束的原因

 

前言       

        线性回归模型是用一条曲线去拟合一个或多个自变量 x 与因变量 y 之间关系的模型，若曲线是一条直线或超平面（成直线时是一元线性回归，成超平面时是多元线性回归）时是线性回归，否则是非线性回归，常见的非线性回归有多项式回归和逻辑回归。线性回归是有监督学习，有标签（可以理解为样本有y值）。通过学习样本 学习映射，得到预测的结果是连续值变量，这是简单的一元线性回归模型，多元线性回归模型后面会详细讲（两者的异同可以参考博文）。线性回归是基础算法，同时是高级算法的根基，所以有必要掌握它的思想并学会融会贯通。接下来我们将详细学习该算法。

1.  基本形式

      预测函数一般表示式

                                                       

      令=1，可以写成

                                                       

      向量表达式

                                                                  

2.  损失函数

   2.1 损失函数

        线性回归模型是用一条曲线去拟合x与y之间的关系，那拟合的效果的好坏如何去判定呢？这就是我们要提到的损失函数，每个算法的损失函数或许不一样，但我们的目的都是使得损失函数最小化，所以需要找到对应的权重θ使得损失函数最小。下面左图是一个权重下的损失函数图像，右图是两个权重下的损失函数，损失函数是凸函数，都有唯一的最小值点。

 

                                          

     一般将线性回归的损失函数定义为：

                                                       

      下面的损失函数与该形式虽然形式不完全一样，但是含义一样。这里的  是为了求导计算的便利，而  是将损失平均化，消除样本量m带来的影响。 

     是预测值，但因为预测值与实际值之间还是存在一定的差距，如何去确定预测的效果的好坏，需要判定预测值与实际值之间的差距，这差距用误差来表示，即。至于损失函数  为什么需要使用平方和？下面从最小二乘法和极大似然估计两个方面去分析。

     2.1.1 最小二乘法

       误差有正有负，如果直接对求和，则会出现正负抵消的情况，反映不出整体误差情况。如果使用平方和，整体的误差分布不变，所以一般使用平方和做损失函数。

       线性模型用一条直线（平面）拟合数据点，找出一条最好的直线（平面）即要求每个真实点直线（平面）的距离最近。即使得残差平方和（RSS）最小

                                                            

       但由于每个样本的数据量存在较大的差异，为了消除样本量差异的影响，使用最小化均方误差（MSE）拟合

                                                            

       所以得到损失函数

                                                            

       式子中的  是为了求导计算便利添加的。 

     2.1.2 极大似然估计

       误差中，误差是独立同分布的，并且服从均值为0方差为的高斯分布（也称为正态分布）。补充：正态分布的均值和方差取不同值，得到不同的分布图，但均值为0，方差为1的分布称为标准正态分布。

      其中，高斯分布表达式为：

                                                      

     由于误差服从均值为0方差为的高斯分布，所以满足：  

                                                      

     于是得到：

                                                        

      该式子表示和结合后的值与接近的概率，即误差最小的概率，即概率越大，说明预测值与真实值越接近。

由于线性回归模型是一条直线（或超平面）拟合多个点，所以需要满足所有误差取得最小值，即所有概率的乘积最大化，符合似然函数：

                                           

      上式中需要找到能使得概率连乘最大化，也就是预测值与真实值无限接近。

      由于连乘难解，所以需要转化成加法，取对数得：

                                              

                                                                                     

       上面的式子中，第一项是确定值，而第二项是变动值，所以要使得最大，即要使得最小化，于是得到损失函数

                                                              

        同理，消除样本量m带来的影响， 将损失平均化，乘以一个 。

  2.2  正规方程法

       正规方程法有一般形式和矩阵形式。

     2.2.1  一般形式

      简单一元线性回归模型为：

                                                                         

      那么，损失函数如下：

                                                                   

                                                               

    损失函数是关于θ和b的凸函数，当它关于θ和b的导数均为零时，得到θ和b的最优解。

（关于凸函数：对区间[a,b]上定义的函数f，若它对区间中任意两点均有则称 f 为区间[a,b]上的凸函数。U形曲线的函数如通常是凸函数。对实数集上的函数，可通过求二阶导数来判别：若二阶导数在区间上非负，则称为凸函数；若二阶导数在区间上恒大于0，则称为严格凸函数。）

    求解和b使损失函数最小化，对求偏导

                                                               

                                                                              

      令，则得到：

                                                                         

                              （注意：由于下面的计算过程会有双重前m项求和，避免混淆，最好将所有项，特别含b的项）    

        对b求偏导

                                                         

                                                                         

          令，则

                                                         

           解得：

                                                                          

           将（2）式带入（1）式，解得（求解过程可以参考最小二乘法求导）

                                                                      

                                                        

         于是，由求得的和b就可以得到接近真实值的预测值以及拟合直线.

         以上是最小二乘法的一般形式解决简单的线性回归问题，如果对于复杂的多元线性回归，则使用最小二乘法的矩阵形式.

     2.2.2  矩阵形式

          多元线性回归是给定数据集，其中 ，。简单的一元线性回归使用一般形式，而多元线性回归比较复杂，使用矩阵形式表示清晰。为了方便讨论，我们将w和b用向量形式表示  ，同样的，数据集D表示为一个m x (d+1)矩阵X ，即

                                         

                                           

    将标记y也改为向量形式，表示样本到超平面的欧式距离之和为（与 类似）

可参考矩阵推导：

                                                            

                                                                       

    对求导，其中当为满秩矩阵

                                                                                

                                                                            

     令，解得

                                                              

    令，则多元线性回归模型为

                                                             

      这个模型是在当为满秩矩阵的时候得到的，但现实任务中往往不是满秩矩阵。比如变量过多，出现变量多于记录数，即列数多于行数，则不是满秩矩阵，那么就会得到多个解θ（这就像解方程组，未知数x的个数大于方程数，则得不到唯一解）使均方误差最小，但是每个θ的重要性不一样，这就需要引入正则化项，下文会详细讲解。

  2.3  梯度下降法

       前面使用最小二乘法求出使得loss function最小化的参数，而实际问题中常使用梯度下降。首先，最小二乘法是通过平方损失函数建立模型优化目标函数的一种思路，求解最优模型过程便具体化为最优化目标函数的过程；而梯度下降法是最优化目标函数的一种优化算法，具体求解使得目标函数能达到最优或者近似最优的参数集。再者，实际问题中不是满秩矩阵，不可逆，最小二乘法无法解决，而梯度下降法可以。

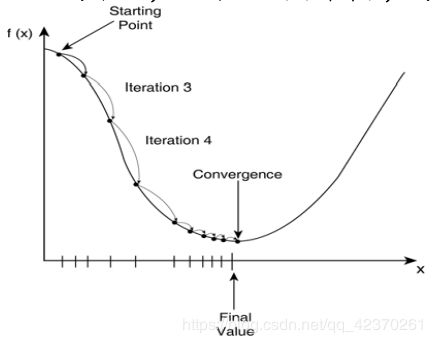
       梯度下降是逐步最小化loss function的过程，如同下山，需要找准方向（斜率或梯度），每次迈进一小步（步长为），直到山底（参考下图理解）。梯度下降式子：    

                                                         

   2.3.1  梯度下降法的代数方式描述

  损失函数的代数表达为： 

                                           

  将   中的 展开

                                    

                                                 

                                                 

       所以θ更新为 

      对每个参数θ求偏导，将所有偏导数写成向量形式，即梯度。该梯度就此次是下降的方向，不断迭代，直到得到全局或局部最优解。

   2.3.2  梯度下降法的矩阵方式描述

  损失函数的向量表达式为：

                                              

   同理，求导 得

                                              

                                             

                                             

                                              

  所以θ更新为：

                                            

       梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

  梯度下降法算法如下：

 输入：目标函数，梯度函数g(x)=▽f(x)，计算精度；

 输出：的极小点.

 （1）取初始值，置

 （2）计算

 （3）计算梯度，当时，停止迭代，令；否则，令，求，使

 （4）置，计算

 当或时，停止迭代，令

 （5）否则，置，转（3）.

   2.3.3  梯度下降的算法调优

     在使用梯度下降算法时需要从以下几个方面进行调优：

 （1）算法步长的选择。

       步长的取值需要根据实际数据样本来决定，可以取一定范围的值来运行，观察损失函数的变化，如果损失函数变小，说明步长合适，否则需要将步长的范围进行调整重新运行。步长需要多次运行观察结果才能确定下来，步长太大迭代过快，可能会错过最优解；而步长太小则迭代太慢，需要时间太长都得不到最优解，所以需要多次运行调试才能找到合适的步长。

 （2）算法参数的初始值选择。

       初始值的不同，得到的最小值也不同，那么得到的就是局部最优解。如果损失函数是凸函数，则一定是最优解。由于梯度下降法可能得到局部最优解而不是全局最优解，所以需要取不同的初始值，然后选择损失函数最小的初始值。

 （3）归一化

      由于样本不同特征取值范围不一样，会造成迭代速度很慢，为了减少特征取值的影响，需要将数据特征归一化（即标准化）。公式为

  2.3.4  梯度下降法的类型（BGD、SBD、MBGD）

 （1）批量梯度下降法

      批量梯度下降法是最常用的一种，该方法在参数更新时使用了所有样本进行更新，前面提到的梯度下降法就是批量下降法。

                                                            

      这里样本数目为m，即使用了所有样本。

 （2）随机梯度下降法

      随机梯度下降法和批量梯度下降法原理类似，不同的是随机梯度下降法在更新参数的时候不是选用所有的m个样本，而是随机选取其中的第i个样本。

                                                            

      上面提到的两种梯度下降法，一个是使用所有样本数据进行梯度下降，另一个是随机选取一个样本进行梯度下降。从训练速度上看，随机梯度下降法只选取其中一个样本进行梯度下降，速度快；而批量梯度下降法是使用所有样本数据进行梯度下降，速度固然慢。但从准确性来看，随机梯度下降法仅仅使用一个样本来决定梯度方向，得到的解不一定是最优解；从收敛速度来看，由于随机梯度下降法是随机选取一个样本方向来决定梯度方向，使得每次参数更新时梯度方向变化较大，不能很快收敛到局部或者全局最优解。既然这两种方法都不完美，那下面我们介绍一种折中的下降法。

 （3）小批量梯度下降法

      小批量梯度下降法是在所有样本m中选取n个数据进行梯度下降，，n的取值根据样本量来决定。

                                                             

      最小二乘法和梯度下降法都是无约束优化算法，但二者存在一定的区别。最小二乘法是计算解析解，适用于较小样本且存在解析解的数据，速度较快；梯度下降法是迭代求解，需要选择步长，适用于较大样本数据。如果较大样本数据使用最小二乘法，需要求一个大矩阵的逆矩阵，需要耗费时间较多，所以选择梯度下降法较好。

     无约束优化算法除了上面提到的最小二乘法和梯度下降法，还有牛顿法和拟牛顿法，具体内容请参考无约束优化算法。

三、欠/过拟合   

       在机器学习模型中，主要任务是在规则化参数的同时最小化误差。最小化误差是为了让我们的模型拟合我们的训练数据，而规则化参数是防止我们的模型过分拟合我们的训练数据。虽然先用train数据训练模型，并尽量使得训练误差最小化，但训练误差最小化不是最终目的。因为模型的真正目的是预测新数据，所以更重要的目的是使得模型的测试误差小，也就是能准确的预测新的样本。

 3.1欠拟合

 3.1.1  何为欠拟合？

      欠拟合就是模型没有很好地捕捉到数据特征，不能够很好地拟合数据。例如本来应该使用一条曲线才能拟合较好得拟合特征，而仅仅使用了一条直线去拟合，则是欠拟合。例如不认真学习数学的同学，平时只记几个公式，考试时答案大部分是不正确的，成绩不理想。

                          

      左图表示Size与Prize关系的数据，中间图是出现欠拟合的模型，不能够很好地拟合数据，如果在中间图的模型后面加一个二次项成曲线，就可以很好地拟合右图中的数据。

 3.1.2  解决方法：

（1）添加特征。欠拟合是因为特征数不够，可以通过组合、泛化、相关性等得到新特征；

（2）添加多项式特征。在机器学习算法普遍使用该方法，如将线性模型通过添加二次项或者三次项使模型泛化能力更强；

（3）减少正则化参数。正则化的目的是用来防止过拟合的，但由于模型出现了欠拟合，则需要减少正则化参数。

 3.2  过拟合

 3.2.1  何为过拟合？

      过拟合：过拟合就是模型把数据特征学习的太彻底，以至于把噪声数据的特征也学习了，这样就会导致在后期测试的时候不能够很好地识别测试数据，使得模型泛化能力太差。就像一位同学临近数学考试前将所有复习题目都背下来，但是考试题目即使类型一样，变量改变也不会解答，从而考试成绩还是不理想。

                    

      左图是欠拟合，而中间图则是拟合得很好，而右图则是过拟合。右图的曲线为了拟合每个特征甚至噪声，变成过度扭曲的曲线。

 3.2.2  解决方法

 （1）重新清洗数据。过拟合的一个原因是数据不纯，所以需要重新清洗数据；

 （2）增大数据的训练量。过拟合的另一个原因是用于训练的数据量太小，训练数据占总数据的比例过小。

 （3）采用正则化方法。正则化方法包括L0正则、L1正则和L2正则，也就是在目标函数后面加上对应的范数，具体知识下面详细讲解。

 （4）采用dropout方法。这个方法在神经网络里面很常用。dropout方法是ImageNet中提出的一种方法，通俗一点讲就是dropout方法在训练的时候让神经元以一定的概率不工作。具体看下图：

                                 
四、正则化（regularization)

      正则化主要是解决过拟合问题，下面对L0、L1和L2范数详细讲解。

 4.1  L0范数   

       L0范数是指向量中非0的元素的个数。那么，在规则化权重矩阵w时，则希望非0元素尽量少，甚至不存在，起到稀疏化矩阵的作用。这比较极端，也是L0较少使用的一个原因。

 4.2  L1范数与Lasso

      L1范数是指向量中各个元素绝对值之和，可以使得权重矩阵w中的元素等于0，也称为“稀疏规则算子”。虽然L0范数和L1范数都可以实现稀疏性，但是因为L0范数不连续，很难优化求解（NP问题），而且L1范数是L0范数的最优凸近似，所以L1范数常被使用。

     假设参数的先验分布是Laplace分布， L1范数的基本形式：

                                                                    

      加入L1范数的线性回归为：

                                                     

      在原来有约束的最小化的loss问题中加入L1范数和拉格朗日乘子，变成无约束的最小化loss问题。
                                              

      我们将L1范数称为loss函数的正则项，也是L1正则化，加入L1范数的线性回归称作LASSO。L1正则化会使不重要的特征的权重置为0，L1范数是稀疏约束，具体情况下面用图形解析。

  L1范数使得参数稀疏主要作用有两方面：

 （1）特征选择：实现特征的自动选择。实际问题中，特征都很多，且存在一些不相关或者包含不重要信息的特征。如果将所有特征都加入模型，则会使得模型求解速度慢。使用L1范数可以进行特征自动选择，主要是将与y不相关或含不重要信息的特征的权重等于0，可以达到去除这些特征，保留重要特征的效果。

 （2）可解释性：去除不重要特征，留下少量的重要特征，解释性更强。

 4.3  L2范数与Ridge

       为了解决L1没有保留局部特征的问题，引入L2范数替代L1范数。L2范数使得权重矩阵w中的元素趋向于0，越小使得模型的复杂度降低。

       L2范数是指向量各元素的平方和然后求平方根。可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0。L2正则项有防止过拟合的作用，原因是它使得参数w变小加剧，且更小的参数值w意味着模型的复杂度更低，对训练数据的拟合刚刚好（奥卡姆剃刀），不会过分拟合训练数据，从而使得不会过拟合，以提高模型的泛化能力。

       假设参数的先验分布是Gaussian 分布，L2范数的基本形式：                           

                                                           

       加入L2范数的线性回归

                                                     

       同样的，也引入拉格朗日乘子λ。

                                                

        加入L2范数的线性回归称作Ridge，L2正则化会使重要性低的特征的权重无线靠近0，但是不为0，L2范数不是稀疏约束。

 4.4 Elastic Net

       Elastic Net 是一种使用L1和L2先验作为正则化矩阵的线性回归模型.这种组合用于只有很少的权重非零的稀疏模型。当多个特征和另一个特征相关的时候弹性网络非常有用。Lasso 倾向于随机选择其中一个，而弹性网络更倾向于选择两个。在实践中，Lasso 和 Ridge 之间权衡，它允许在循环过程中继承 Ridge 的稳定性。

                                          

        Elastic Net在高度相关变量的情况下，会产生群体效应；选择变量的数目没有限制；可以承受双重收缩。

 4.5  L1为稀疏约束的原因

                      

       根据上图，L1范数含绝对值，得到的是左图四边形；而L2范数含平方项，得到的是右图圆形。不同在于L1在和每个坐标轴相交的地方都有”角“出现，与目标函数相交的地方也是在角的位置。角的位置就容易产生稀疏性，例如图中的交点处w1=0。L2就没有这样的性质，因为没有角，相交的位置有稀疏性的概率就非常低，从直观上解释了为什么L1能够产生稀疏性而L2就不行。

      本篇博文主要是线性回归模型的理论知识，关于线性回归算法的代码会在下一篇博文中展示。

参考资料：

1.梯度下降法：https://www.cnblogs.com/pinard/p/5970503.html

2.机器学习---周志华

3.矩阵求导：https://blog.csdn.net/nomadlx53/article/details/50849941