聚类分析及R实现
一、聚类分析的概念
聚类分析时一种原理简单、应用广泛的数据挖掘技术。聚类分析即是把若干事务按照某种标准归为几个类别,其中较为相近的聚为一类,不那么相近的聚于不同类
聚类分析时研究对样本或变量的聚类,在进行聚类时,可使用的方法有很多,而这些方法的选择往往与变量的类型有关,由于数据的来源及测量方法的不同,变量大致可以分为两类:
定量变量;定性变量
二、聚类算法
聚类算法种类繁多,其中绝大多数可以用R实现,下面将选取普及型最广,最实用,最具有代表性的5种聚类算法进行介绍,其中包括:
K-均值聚类(K-means)
K-中心点聚类(K-Medoids)
密度聚类(Densit based Spatial Clustering of Application with Noise,DBSCAN)
层次聚类(系谱聚类 Hierarchical Clustering,HC)
期望最大化聚类(Expectation Maximization,EM)
需要说明的是,这些算法本身无所谓优劣,而最终运用于数据的效果却存在好坏差异,这在很大程度上取决于数据使用者对于算法的选择是否得当。
1.K-均值聚类
K-均值算法是最早出现的聚类算法之一,它是一种快速聚类方法,但对于异常值或极值敏感,稳定性差,因此适合处理分布集中的大样本数据集
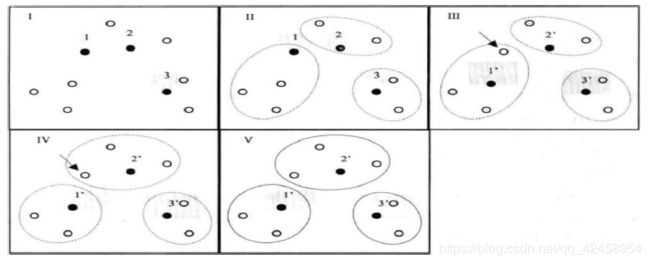
她的思路是以随机选取的K(预设类别数)个样本作为起始中心点,将其余样本归入相似度最高中心点所在的簇(cluster),再确立当前簇中样本坐标的均值为新的中心点,依次循环迭代下去,直至所有样本所属类别不再变动。算法的计算过程非常直观,下图为10个点聚为3类为例展示算法步骤。
2.K-中心值聚类
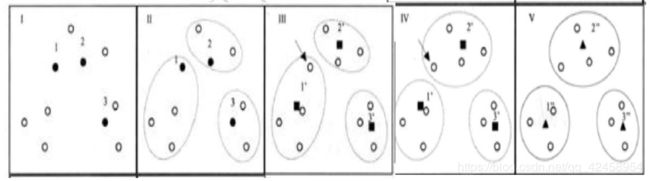
K-中心点算法与K-均值算法在原理上十分相近,它是针对K-均值算法易受极值影响这一缺点的改进算法,在原理上的差异在于选择各类别中心点时不取样本均值点,而在类别内选取到其余样本距离之和最小的样本为中心。
3.层次聚类
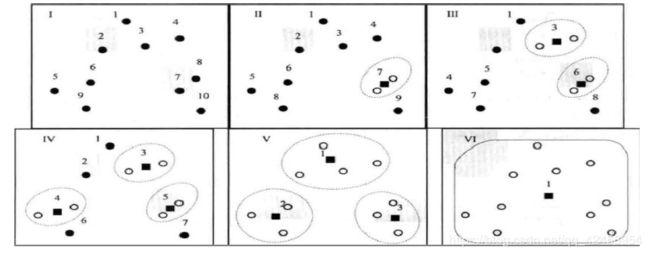
层次聚类的名称在于,其聚类的过程可以通过类似于系谱图的形式呈现出来。相比K-均值算法与K-中心点算法,系谱算法的突出特点在于,不需要先设定类别数K,这是因为它每次迭代过程仅将距离最近的两个样本/簇聚为一类,其运作过程将自然得到k=n至k=1(n为待分类样本总数)个类别的聚类结果。
4.连续变量距离
对于连续性变量数据,有一些典型的距离定义
Dist函数
在R语言中,使用dist函数可以把一个矩阵或数据框转化为距离矩阵。
dist(x, method = "euclidean", diag = FALSE, upper = FALSE, p=2)
连续性变量距离的去量纲处理
- 对连续性变量的距离计算,实际存在一个量纲问题
- 所谓量纲,就是指标的单位
5. R中的实现
Kmeans函数
K 均值算法在 R 语言中实现的核心函数为 kmeans(), 来源于 stats 软件包。该函数的基本格式为:
kmeans(x, centers, iter.max = 10, nstart = 1, algorithm = c("Hartigan Wong", "Lloyd",
"Forgy","MacQueen"), trace=
其中 x 为进行聚类分析的数据集; centers 为预设类别数 k iter.max 为迭代的最大值,且默认值
为 10 nstart 为选择随机起始中心点的次数,默认取 1 ;而参数 algorithm 则提供了 4 中算法选择,
默认为 Hartigan Wong 算法。
hclust、cutree及rect.hclust函数
这三个函数都来源于 stat 软件包,在系谱聚类过程中发挥着各自不同的作用。
核心函数为 hclust()hclust(),用来实现系谱聚类算法,其基本格式十分简单,仅含有三个参数
hclust(d, method = “complete”, members = NULL)
其中, d 为待处理数据集样本间的距离矩阵,可用 dist() 函数计算得到; method 参数用于选
择聚类的具体算法,可供选择的有 ward 、 single 及 complete 等 7 中,默认选择 complete 方法;
参数 members 用于指出每个待聚类样本点 簇是由几个单样本构成,该参数默认值为 NULL
表示每个样本点本身即为单样本 。
而 cutree() 函数则可以对 hclust() 函数的聚类结果进行剪枝,即选择输出指定类别数的系谱聚
类结果。其格式为: cutree(tree,k=NULL,h=NULL)
函数 rect.hclust() 可以在 plot() 形成的系谱图中将指定类别中的样本分支用方框表示出来,十
分有助于直观分析聚类结果。其基本格式为:
rect.hclust(tree, k = NULL, which = NULL, x = NULL, h = NULL, border = 2, cluster = NULL)
层次聚类方法