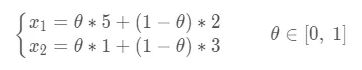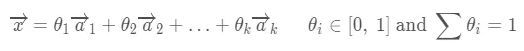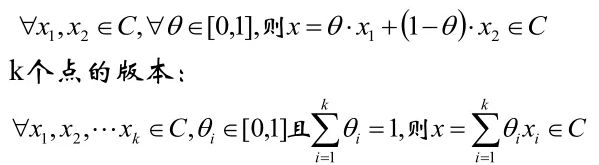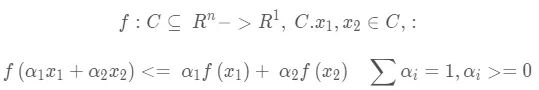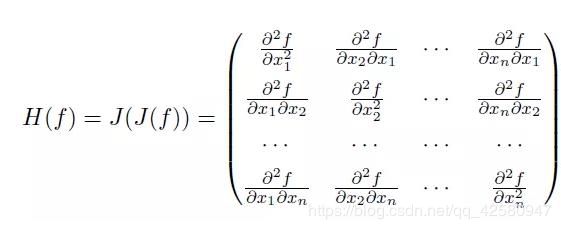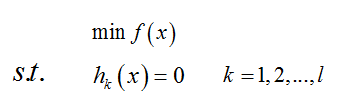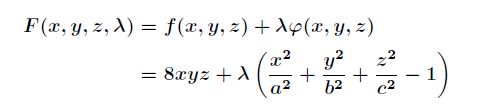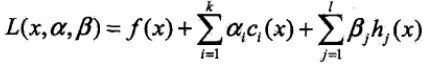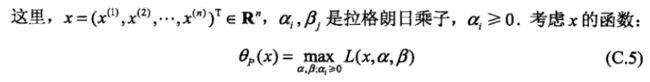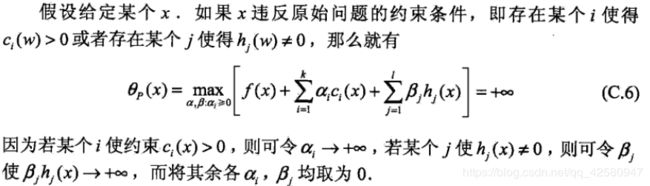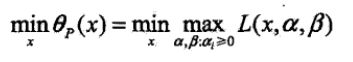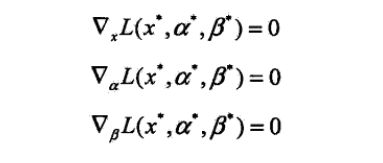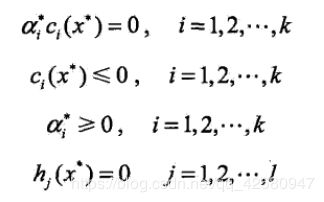机器学习中的数学(七)--凸优化的基础知识
写在前面
《机器学习中的数学》系列主要列举了在机器学习中用到的较多的数学知识,包括微积分,线性代数,概率统计,信息论以及凸优化等等。本系列重在描述基本概念,并不在应用的方面的做深入的探讨,如果想更深的了解某一方面的知识,请自行查找研究。
1.几何体的向量表示
已知二维平面上两定点A(5,1),B(2,3),给出线段AB的方程表示如下:
如果将点A看成向量A,点B看成向量b,则线段AB的向量表示为:
直线的向量表示是:
![]()
通过刚刚的二维平面我们可以推广到多维空间
三角形
三维平面
超几何体的向量表示
超平面的向量表示
2. 凸集
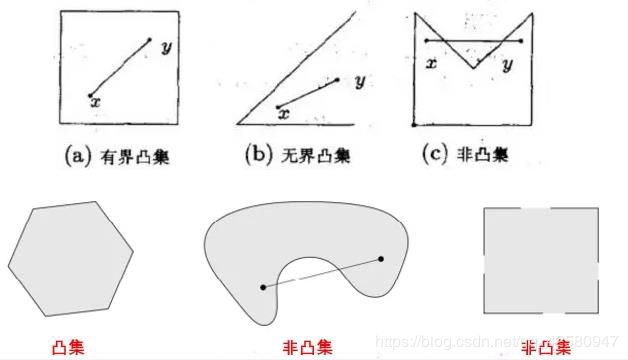
集合 C内任意两点间的线段也均在集合 C内,则称集合 C为凸集,数学定义为:
上面凸集定义中便用到了线段的向量表示,含义是如果点x1和点x2在集合C内,则线段x1,x2上所有的点都在集合C内,凸集的交集仍是凸集。
3. 凸函数
3.1 凸函数的定义
凸函数的定义:
则成f(x)为定义在凸集C上的凸函数
严格的凸函数的定义为:设f∈Rn->R1,C是凸集,对于x1,x2∈C,都有:
则f(x)为定义在凸集C上的严格凸函数。
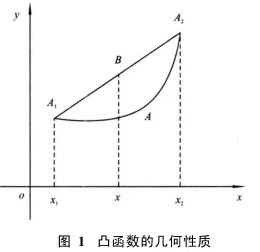
3.2 凸函数定义的几何解释
设A1 、A2 是凸函数曲线上的两个点,他们对应的横坐标 x1
因此,凸函数的几何含义是:任意两点 A1 和A2 之间的部分位于弦A1A2的下方或曲线任 一点切线上方,不严谨的一个说法:割始终位于两点间函数曲线的上方。
4. 凸函数的各种性质及其证明
4.1 凸优化问题的局部极小值是全局极小值
这个性质是凸优化问题一个良好的性质,在机器学习任务中我们只需将非凸问题转化为凸优化问题,便可直接求出问题的全局极值。
证明如下:
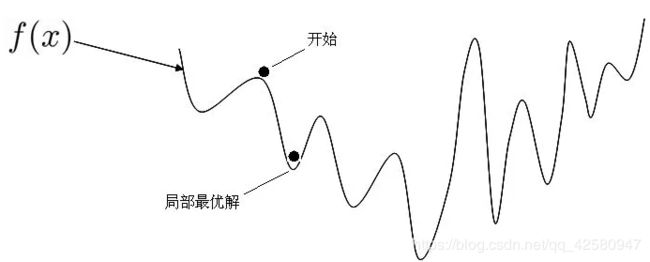
从下图可以看出当函数不是凸函数时,对非凸函数f(x) 进行最优化时,便可能得到局部最优解,无法获得全局最优解。
f为凸函数的充要条件是:对于 ∀x1, x2∈C x1, x2∈C 且x1≠x2 都有,
看上图,凸函数 f(x) ,在函数 f(x) 上取一点 (x, f(x)) (x, f(x)) 做曲线的切线,斜率为 k,可以看出对于凸函数 f(x) 来说,切线始终是凸函数 f(x) 的下界,我们看点 A、B,B是曲线上一点, A点是切线上一点,且 A、B的横坐标都为y,则B点的纵坐标始终大于 A点的纵坐标。
4.2 凸函数其Hessian矩阵半正定
Hessian矩阵是一个多元函数的二阶偏导构成方阵
证明:
何为半正定矩阵:其特征值都是非零的,正定矩阵的特征值都是正数
4.3 对于凸函数f(x),其中Q1+Q2+Q3+...+Qn=1,0<=Qi<=1,则有:
证明:
4.4 Jessen不等式
f(x) 为凸函数,其中 E(x)是x的期望
证明如下:
5. 约束条件
5.1 无约束条件
这是最简单的情况,解决方法通常函数对变量求导,令求函数等于 0的点可能是极值。将结果带回原函数进行验证即可。
5.2 等式约束条件
解决方法是消元或者拉格朗日。消元法比较简单不在赘述,这里主要讲拉格朗日法,因为后面提到的KKT条件是对拉格朗日乘子法的一种泛化。
举例:
当然这个问题实际可以先根据条件消去z(消元法),然后带入转化为无条件极值问题来处理,首先定义拉格朗提函数F(x):
然后分别求偏导。
5.3 不等式约束条件
设目标函数f(x),不等式约束为g(x),有的教程还会添加上等式约束条件h(x),此时的约束优化问题为:
其中f(x)是原目标函数,ci(x)是第i个不等式约束条件,ai是对应的约束系数,hj是不等式约束,Bj是对应的约束系数:
6.KKT
KKT是原问题转化为对偶优化问题的必要条件,但不是充分条件。只有在求解一个凸优化问题时,才是充分必要条件。
KKT的条件是: