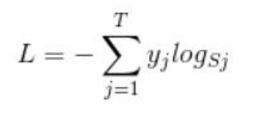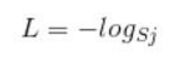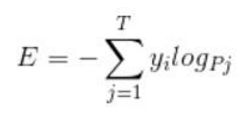TensorFlow学习笔记——LeNet-5（训练自己的数据集）

　　在之前的TensorFlow学习笔记——图像识别与卷积神经网络（链接：请点击我）中了解了一下经典的卷积神经网络模型LeNet模型。那其实之前学习了别人的代码实现了LeNet网络对MNIST数据集的训练。而这篇文章是想自己完成LeNet网络来训练自己的数据集。LeNet主要用来进行手写字符的识别与分类，下面记录一下自己学习的过程。

　　我的学习步骤分为以下四步：

• 1，温习LeNet-5的网络层
• 2，使用LeNet-5训练MNIST数据集
• 3，使用LeNet-5训练TFRecord格式的MNIST数据集
• 4，使用LeNet-5训练自己的数据集（TFRecord格式）

　　LeNet是出自论文Gradient-Based Learning Applied to Document Recognition，是一种用于手写体字符识别的非常高效的卷积神经网络。那我要训练的是印刷体的数字和字母，可能难点就是字母大小尺寸不一。下面我尝试使用LeNet-5来进行识别。首先学习其网络结构。

1，LeNet-5的网络层解析

　　LeNet-5这个网络虽然很小，但是包含了深度学习的基本模块：卷积层，池化层，全连接层。是其他深度学习模型的基础。LeNet网络奠定了现代卷积神经网络的基础。LeNet-5模型总共有7层，这里我们对LeNet-5进行深入分析。

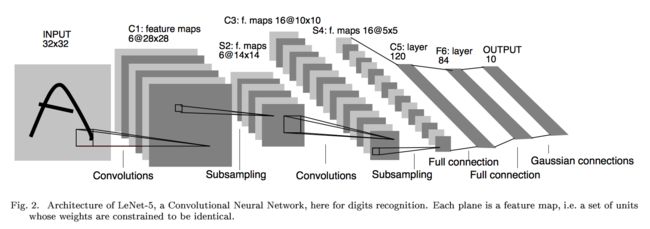
　　下图展示了以MNIST数据集为例的LeNet-5模型架构：

 　　下面再啰嗦一次。

第一层：卷积层（C1层）

　　这一层为原始的图像元素，LeNet-5模型接受的输入层大小为32*32*1，第一层卷积层过滤器的尺寸为5*5，深度为6，不使用全0填充，所以这一层的输出的尺寸为32-5+1=28面四个并打印为6，这一个卷积层总共有5*5*1*6+6=156个参数，其中6个未偏置项参数，因为下一层的节点矩阵有28*28*6=4704个结点，每个节点和5*5=25个当前层节点相连，每个神经元对应一个偏置项（这就是5*5+1的原因）所以本卷积层共有（5*5+1）*6*（28*28）=122304个连接。

　　那么也就是说，过滤器尺寸为[5, 5]，通道为1，深度为6。（除去输入层和输出层，我们有六个特征平面，包括两个卷积层，两个池化层，两个全连接层），特征图有6个，说明6个不同的卷积核，所以深度为6。

第二层：池化层（S2层）

　　池化层又叫做下采样层，目的是压缩数据，降低数据维度。

　　这一层的输入为第一层的输出，是一个28*28*6的节点矩阵，本层采用的过滤器大小为2*2，长和宽的步长均为2，所以本层的输出矩阵大小为14*14*6

　　6个14*14的特征图，每个图中的每个单元与C1特征图中的一个2*2邻域相连接，不重叠。因此S2中每个特征图的大小是C1中特征图大小的1/4。

第三层：卷积层（C3层）

　　本层输入的矩阵大小为14*14*6，使用的过滤器大小为5*5，深度为16.本层不使用全0填充，步长为1.本层的输出矩阵大小为10*10*16。按照标准的卷积层，本层应该有5*5*6*16+16=2416个参数，10*10*16*（25+1）=41600个连接。

第四层：池化层（S4层）

　　本层的输入矩阵大小为10*10*16，采用的过滤器大小为2*2，步长为2，本层的输出矩阵大小为5*5*16

第五层：全连接层（C5层）

　　本层的输入矩阵大小为5*5*16，在LeNet-5模型的论文中将这一层称为卷积层，但是因为过滤器的大小就是5*5，所以和全连接层没有区别，在之后的TensorFlow程序实现中也会将这一层看成全连接层。如果将5*5*16矩阵中的节点拉成一个向量，那么这一层和之前学习的全连接层就是一样的了。

　　本层的输出节点个数为120个，总共有5*5*16*120+120=48120个参数。

　　这一层还是卷积层，且有120个神经元，可以看做是120个特征图，每张特征图的大小为5*5，每个单元与S4层的全部16个单元的5*5领域相连，因此正好和池化层匹配（S4和C5之间的全连接）。

第六层：全连接层（F6层）

　　本层的输入节点个数为120个，输出节点个数为84个，总共参数为120*84+84=10164个。

　　之所以有84个单元，是因为输出层的设计，与C5层全相连，F6层计算输入向量和权重向量之间的点积，再加上一个偏置，所以84=7*12

第七层：全连接层（F7层）

　　本层的输入节点个数为84个，输出节点为10个，总共参数为84*10+10=850个。

　　该层有十个神经元，可以理解这是对于手写体10个数，哪个输出的数大，那个神经元代表的数字就是输出。

1，卷积层tf.nn.conv2d()

　　函数类型如下：

1 2 3 4 5 6 7 8 9 10

def conv2d(  # pylint: disable=redefined-builtin,dangerous-default-value     input,     filter=None,     strides=None,     padding=None,     use_cudnn_on_gpu=True,     data_format="NHWC",     dilations=[1, 1, 1, 1],     name=None,     filters=None):

　　参数说明：

• data_format：表示输入的格式，有两种分别为：“NHWC”和“NCHW”，默认为“NHWC”

• input：输入是一个4维格式的（图像）数据，数据的 shape 由 data_format 决定：当 data_format 为“NHWC”输入数据的shape表示为[batch, in_height, in_width, in_channels]，分别表示训练时一个batch的图片数量、图片高度、 图片宽度、 图像通道数。当 data_format 为“NHWC”输入数据的shape表示为[batch, in_channels， in_height, in_width]

• filter：卷积核是一个4维格式的数据：shape表示为：[height,width,in_channels, out_channels]，分别表示卷积核的高、宽、深度（与输入的in_channels应相同）、输出 feature map的个数（即卷积核的个数）。

• strides：表示步长：一个长度为4的一维列表，每个元素跟data_format互相对应，表示在data_format每一维上的移动步长。当输入的默认格式为：“NHWC”，则 strides = [batch , in_height , in_width, in_channels]。其中 batch 和 in_channels 要求一定为1，即只能在一个样本的一个通道上的特征图上进行移动，in_height , in_width表示卷积核在特征图的高度和宽度上移动的布长，即 。

• padding：表示填充方式：“SAME”表示采用填充的方式，简单地理解为以0填充边缘，当stride为1时，输入和输出的维度相同；“VALID”表示采用不填充的方式，多余地进行丢弃。

2，池化层 tf.nn.max_pool()  /  tf.nn.avg_pool()

• value：表示池化的输入：一个4维格式的数据，数据的 shape 由 data_format 决定，默认情况下shape 为[batch, height, width, channels]

• ksize：表示池化窗口的大小：一个长度为4的一维列表，一般为[1, height, width, 1]，因不想在batch和channels上做池化，则将其值设为1。

• 其他参数与上面类似。

3，softmax函数

　　举个简单的例子，假设一个五分类，然后一个样本I的标签  y = [0, 0, 0, 1, 0]，也就是说样本I的真实标签是4，假设模型预测的结果概率（softmax的输出）p=[0.1,0.15,0.05,0.6,0.1]，可以看出这个预测是对的，那么对应的损失L=-log(0.6)，也就是当这个样本经过这样的网络参数产生这样的预测p时，它的损失是-log(0.6)。那么假设p=[0.15,0.2,0.4,0.1,0.15]，这个预测结果就很离谱了，因为真实标签是4，而你觉得这个样本是4的概率只有0.1（远不如其他概率高，如果是在测试阶段，那么模型就会预测该样本属于类别3），对应损失L=-log(0.1)。那么假设p=[0.05,0.15,0.4,0.3,0.1]，这个预测结果虽然也错了，但是没有前面那个那么离谱，对应的损失L=-log(0.3)。我们知道log函数在输入小于1的时候是个负数，而且log函数是递增函数，所以-log(0.6) < -log(0.3) < -log(0.1)。简单讲就是你预测错比预测对的损失要大，预测错得离谱比预测错得轻微的损失要大。

 　　下面简单说一下损失函数 softmax loss：

 　　首先，L是损失，Sj是softmax的输出向量S的第j个值，那Sj表示这个样本属于第j个类别的概率。yj 前面有个求和符号，j的范围是1~T（即类别1到类别T），因此y是一个1*T的向量，里面的T个值，而且只有1个值是1，其他 T-1个值都是0，那么那个位置的值是1呢？真实标签对应的位置的那个值是1，其他都是0，所以这个公式可以改为：

 　　当然，此时要限定 j是指当前样本的真实标签。

4，cross  entropy交叉熵

　　损失函数是在训练过程中，得到的输出值与理想输出值的差距，这里有很多衡量的标准，比如均方误差的方法，也就是输出值和理想值的方差来表示：

1	loss = tf.reduce_mean(tf.square(yout - Y))

　　公式如下：

 　　TensorFlow使用的函数如下：

1	tf.nn.dropout(x, keep_prob, noise_shape=None, seed=None,name=None)

　　参数意义：

• 第一个参数x：指输入　
• 第二个参数keep_prob: 设置神经元被选中的概率,在初始化时keep_prob是一个占位符,  keep_prob = tf.placeholder(tf.float32) 。tensorflow在run时设置keep_prob具体的值，例如keep_prob: 0.5
• 第五个参数name：指定该操作的名字。

5，执行训练

　　执行训练的过程就是让已有的输入和输出数据一次又一次的填入模型中，根据数据进行训练。什么时候进行呢？那就是需要搭建一个平台，让它在这个平台上运行，这个平台叫做会话，tf.Session()，就好比你修好了路，当然不作为摆设，你要在某个时间段内开始通车。

1 2 3 4

with tf.Session() as sess:     sess.run(tf.global_variables_initializer())     for i in range(1000):         sess.run(optimizer, feed_dict = {X : x, Y : y})

　　

6，LeNet-5的局限性

　　卷积网络在本质上是一种输入到输出的映射，它能够学习大量的输入与输出之间的映射关系，而不需要任何输入和输出之间的精确的数学表达式。

　　CNN能够得出原始图像的有效表征，这使得CNN能够直接从原始像素中，经过极少的预处理，识别视觉上面的规律。然而，由于当时缺乏大规模训练数据，计算机的计算能力也跟不上，LeNet-5对于复杂问题的处理结果并不理想。

　　2006年起，人们设计了很多方法，想要克服难以训练深度CNN的困难。其中，最出名的时，Krizhevsky et al 提出了一个经典的CNN结构，并在图像识别任务上取得了重大突破，其方法的整体框架叫做AlexNet，与LeNet-5类似，但是要加深一点，此后深度卷积如雨后春笋一般，出现了很多。

 

 2，Lenet-5实现MNIST数据训练（使用官方格式数据）

　　首先，我们热个手，使用MNIST数据的官方格式，直接进行训练。这里数据没有进行处理，也没有转化。

　　代码：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

# _*_coding:utf-8_*_ ''' LeNet是第一个成功应用于数字识别问题的卷积神经网络 LeNet模型总共有7层，在MNIST上LeNet-5模型可以达到99.2%的正确率 ''' import tensorflow as tf import tensorflow.examples.tutorials.mnist.input_data as input_data import time import os   os.environ['CUDA_VISIBLE_DEVICES'] = '1,2'     # 获取mnist数据 mnist_data_set = input_data.read_data_sets('MNIST_data', one_hot=True) # 声明输入图片数据类型，mnist的手写体图片大小为28*28=784 # None表示行向量的维度是任意的，也就是一次可以输出多张图片 # placeholder 基本都是占位符，先定义，后面会用到的 x = tf.placeholder('float', [None, 784]) # y_为网络的输出,数字十个类别 y_ = tf.placeholder('float', [None, 10])   # 把输入的数据转变成二维形式，用于卷积计算 # -1表示一次可以存储多张照片，1表示图像的通道数为1 x_image = tf.reshape(x, [-1, 28, 28, 1])   # 卷积核初始化，大小为6个5*5的卷积核，1和x_image的1对应，即为图像的通道数 filter1 = tf.Variable(tf.truncated_normal([5, 5, 1, 6])) # 偏置项 bias1 = tf.Variable(tf.truncated_normal([6])) # 二维卷积计算 conv1 = tf.nn.conv2d(x_image, filter1, strides=[1, 1, 1, 1], padding='SAME') h_conv1 = tf.nn.sigmoid(conv1 + bias1) # 池化层 maxPool2 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')   filter2 = tf.Variable(tf.truncated_normal([5, 5, 6, 16])) bias2 = tf.Variable(tf.truncated_normal([16])) conv2 = tf.nn.conv2d(maxPool2, filter2, strides=[1, 1, 1, 1], padding='SAME') h_conv2 = tf.nn.sigmoid(conv2 + bias2)   maxPool3 = tf.nn.max_pool(h_conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')   filter3 = tf.Variable(tf.truncated_normal([5, 5, 16, 120])) bias3 = tf.Variable(tf.truncated_normal([120])) conv3 = tf.nn.conv2d(maxPool3, filter3, strides=[1, 1, 1, 1], padding='SAME') h_conv3 = tf.nn.sigmoid(conv3 + bias3)   # 全连接层，权重初始化 W_fc1 = tf.Variable(tf.truncated_normal([7 * 7 * 120, 80])) # 偏置项 b_fc1 = tf.Variable(tf.truncated_normal([80])) # 将卷积的输出展开 h_pool2_flat = tf.reshape(h_conv3, [-1, 7 * 7 * 120]) h_fc1 = tf.nn.sigmoid(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)   W_fc2 = tf.Variable(tf.truncated_normal([80, 10])) b_fc2 = tf.Variable(tf.truncated_normal([10])) # 输出层，使用softmax进行多分类 y_conv = tf.nn.softmax(tf.matmul(h_fc1, W_fc2) + b_fc2)   # 损失函数，交叉熵 cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv)) # 使用梯度下降法来更新权重，学习速率为0.001，改为0.01的话会导致权重更新有问题，准确率会滴 train_step = tf.train.GradientDescentOptimizer(0.001).minimize(cross_entropy)   sess = tf.InteractiveSession()   # 测试准确率，tf.argmax() 计算行或列的最大值，返回最大值下标的向量 # tf.equal() 计算两个向量对应的元素是否相等，返回数据为bool # tf.cast() 把bool数据转化为浮点型 correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, 'float'))   # 对所有变量进行初始化 sess.run(tf.global_variables_initializer())   start_time = time.time() for i in range(50000):     # 获取训练数据，每次100张     # 我们后面取数据的时候，直接获取feed_dict={x: batch[0], y_true: batch[1]}     # batch = mnist_data_set.train.next_batch(60)     batch_xs, batch_ys = mnist_data_set.train.next_batch(100)     train_step.run(feed_dict={x: batch_xs, y_: batch_ys})     # 每个100次输出当前的准确率     if i % 100 == 0:         train_accuracy = accuracy.eval(feed_dict={x: batch_xs, y_: batch_ys})         print('step %d, training accuracy %g' % (i, train_accuracy))         # 计算时间间隔         end_time = time.time()         print('time: ', (end_time - start_time))         start_time = end_time   print("Test accuracy: {}".format(accuracy.eval(session=sess,                                                feed_dict={                                                    x: mnist_data_set.test.images,                                                    y_: mnist_data_set.test.labels})))   # 关闭会话 sess.close()

　　训练过程如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

step 48200, training accuracy 1 time:  0.240248441696167 step 48300, training accuracy 1 time:  0.24075675010681152 step 48400, training accuracy 1 time:  0.3005177974700928 step 48500, training accuracy 1 time:  0.2406449317932129 step 48600, training accuracy 1 time:  0.24107027053833008 step 48700, training accuracy 0.99 time:  0.24148797988891602 step 48800, training accuracy 0.98 time:  0.24003911018371582 step 48900, training accuracy 0.99 time:  0.23934340476989746 step 49000, training accuracy 1 time:  0.28536438941955566 step 49100, training accuracy 0.98 time:  0.24154186248779297 step 49200, training accuracy 1 time:  0.24214410781860352 step 49300, training accuracy 0.96 time:  0.24277353286743164 step 49400, training accuracy 1 time:  0.2415931224822998 step 49500, training accuracy 1 time:  0.2908365726470947 step 49600, training accuracy 1 time:  0.24100923538208008 step 49700, training accuracy 1 time:  0.2422494888305664 step 49800, training accuracy 1 time:  0.24294066429138184 step 49900, training accuracy 0.99 time:  0.24169301986694336 Test accuracy: 0.9772999882698059

　　训练的准确率基本在98%~100%之间，并且测试集达到了97.7%的准确率，效果还是不错的。

　　注意：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

# *****************   改进1  ***************** x = tf.placeholder('float', shape=[None, 28 * 28]) y_ = tf.placeholder('float', shape=[None, 10])   # 当然这里定义数据类型的时候也可以这样写 x = tf.placeholder(tf.float32, [None, 784]) y_ = tf.placeholder(tf.float32, [None, 10])     # *****************   改进2  ***************** train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy) #这里用Ａdam优化器优化函数　也可以使用随机梯度下降优化函数 learning_rate = 0.001 optimizer= tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)     # *****************   改进3  ***************** # 通过tf.reshape函数将第五层的输出变成一个batch的向量 # reshaped = tf.reshape(relu3, [pool_shape[0], nodes])      改为：（不然会报错） reshaped = tf.layers.flatten(relu3)

　　

3，使用LeNet-5训练MNIST数据集（将MNIST数据转化为TFRecord格式）

　　大多数书上和网络上实例就是使用已经封装好的mnist数据集来训练卷积神经网络。但是这里我想用神经网络来训练自己的数据集，所以如何将自己的数据集导入神经网络？这里我首先将MNIST数据转化为TFRecord数据格式进行训练，下一步训练自己的数据集。

　　我的解决思路如下：

1，将自己的数据集转换为TensorFlow支持的神经网络输入格式TFRecord。

2，重建LeNet-5卷积神经网络

3，对神经网络进行训练

1，制作TFRecord的MNIST数据集

　　首先，将自己的数据集转化为TFRecord，我之前的博客有说，这里不再学习。

　　想学习，请参考博客：高效读取数据的方法（TFRecord）

　　将MNIST数据集中的所有文件存储到一个TFRecord文件中，然后我们用的时候，直接读取封装好的MNIST数据的TFRecord文件。

 　　但是后面需要使用如何读取TFRecord文件的函数，这里注意，你生成TFRecord文件的函数和读取的函数一定要保持一致，不然会报错。

　　将MNIST数据集格式转化为TFRecord格式，前面有讲过，这里不再赘述。

　　想学习，请参考博客：使用TensorFlow操作MNIST数据（2）